Законы распределения дискретных случайных величин

Производятся испытания, в каждом из которых может появиться событие А или событие .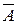

Биномиальным (законом распределения Бернулли) называют закон распределения дискретной случайной величины Х – числа появлений события А в n независимых испытаниях, в каждом из которых вероятность появления события равна р. Вероятность возможного значения Х = т (числа т появлений события) вычисляют по формуле Бернулли:

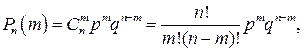(5.1)

где q=1–р – это вероятность не наступления события А (появления события 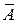). Ряд распределения случайной величины Х, распределенной по биномиальному закону (закону распределения Бернулли) имеет вид:

xi				…	n	,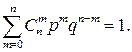
pi				…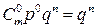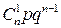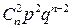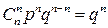

Функция распределения: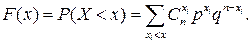

Математическое ожидание и дисперсия случайной величины, распределенной по биномиальному закону, соответственно равны: М(Х)=np, D(X)=npq.

Наивероятнейшее число m₀ появлений событий в n независимых испытаниях определяется по формуле:

nр - q£ m₀ £ np+р (5.2)

Если число испытаний велико, а вероятность появления события р в каждом испытании мала, то вероятность того, что некоторое событие появиться m раз в n испытаниях, приближенно вычисляется по формуле Пуассона:

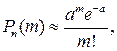(5.3)

где m – число появлений событий в n независимых испытаниях, a=nр – среднее число появлений события в n испытаниях.

Ряд распределения случайной величины Х, распределенной по закону Пуассона имеет вид:

хm				…	m	…	,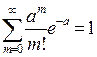
				…		…

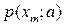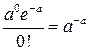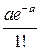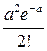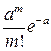Если известно среднее число событий 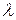, которые появляются в единицу времени, то вероятность появления m событий простейшего потока событий за время t, вычисляется по формуле: .

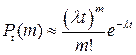Функция пуассоновского распределения: .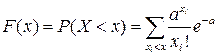

Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона равны одному и тому же числу а: М(Х)=D(Х)= а, a=np.

Геометрическое распределение возникает в том случае, когда производится серия испытаний до первого появления события А. Тогда распределение случайной величины Х имеет вид:

xi				…	m	...
pi	p	qp	q2p	...	qm-1p	…

Вероятность появления события А в каждом испытании постоянна и равна р, т.е. р=Р(А), и .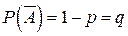

Функция геометрического распределения: .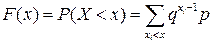

Математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины Х, распределенной по геометрическому закону, соответственно равны: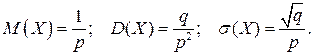

Гипергеометрический закон распределения используется при проверке качества продукции. Пусть проверяется N изделий, и известно, что среди этих изделий имеется М изделий, которые обладают некоторым признаком 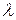, а остальные (N–М) – признаком 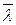. Для проверки производится выборка, содержащая п изделий. Для определения вероятности того, что среди этих изделий т изделий обладают некоторым признаком 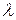(событие А), используется классический способ задания вероятности. Число элементарных событий пространство элементарных событий Ω и события А определятся числом сочетаний 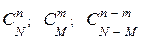, а искомая вероятность вычисляется по формуле:

,

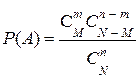где А – событие, состоящее в том, что в выборке т объектов обладают признаком .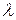

Закон распределения дискретной случайной величины Х, характеризующей число появлений события А т раз в N испытаниях имеет вид:

– если п £ М	xi				…	п
pi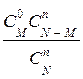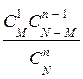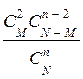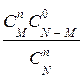

– если п > М	xi			…	М
pi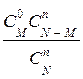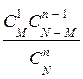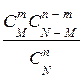

Функция гипергеометрического распределения:

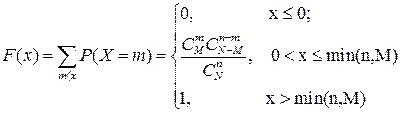
Гипергеометрический закон стремится к биномиальному закону распределения, при N®∞, если 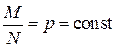. Его числовые характеристики равны: .

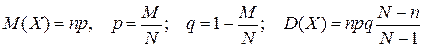Задачи

5.1.Вероятности рождения мальчика и девочки можно считать равными 0,5. Какова вероятность того, что среди 6 наудачу отобранных новорожденных будет: а) хотя бы один мальчик – событие А; б) число мальчиков и девочек одинаково – событие В; в) мальчиков больше, чем девочек – событие С?

Решение. Введем случайную величину Х – число мальчиков среди 6 новорожденных. Так как при каждом рождении вероятность рождения мальчика постоянна, то эта случайная величина подчиняется биномиальному закону распределения, т.е. согласно формуле (5.1) вероятность того, что случайная величина Х примет значение m будет равна:

.

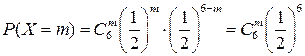Событию А ={среди 6 новорожденных будет хотя бы один мальчик} противоположно событию 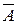= {среди 6 новорожденных не будет ни одного мальчика}. Вероятность события 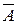найти проще, поэтому

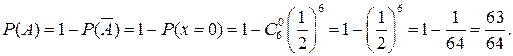
Вероятность события В вычислим по формуле (5.1):

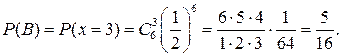
Событие С произойдет, если среди 6 новорожденных будет 4 мальчика или 5 или 6, т.е. {Х>3}. Нетрудно увидеть, что

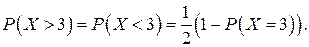
Таким образом,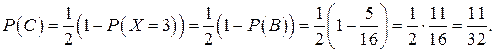

Ответ: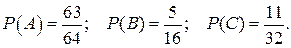

5.2.Два равносильных шахматиста договорились сыграть 4 результативных партий. Ничьи не учитываются и считается, что каждый из участников может выиграть очередную партию с вероятностью 0,5. Определить вероятность выигрыша одного из шахматистов (выигравшим матч считается тот, кто победит в большем числе партий).

Решение. Во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, поэтому случайная величина Х – число выигранных партий, подчиняется биномиальному закону распределения. Один из шахматистов победит, если выиграет 3 или 4 партии. Воспользуемся формулой (5.1) и вычислим вероятности Р₄(3) и Р₄(4):

.

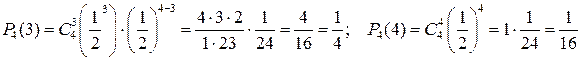Тогда, применив теорему сложения, получим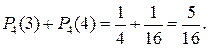

Ответ: вероятность выигрыша одного из шахматистов равна: .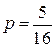

5.3.В партии 10% нестандартных деталей. Наудачу отобраны 4 детали. Написать биномиальный закон распределения дискретной случайной величины Х – числа нестандартных деталей среди 4-х отобранных и построить многоугольник полученного распределения. Вычислить М(Х); D(Х); σ(Х); F(х).

5.4.В банк подано 5 заявок фирм на получение кредита. Вероятность получить кредит для каждой из фирм равна 2/3. Найти вероятность того, что из пяти фирм кредит получит а) ровно 1 фирма; б) по крайней мере 2; в) ровно 3; г) больше чем 3 фирмы.

5.5.Десять осветительных лампочек для елки включены в цепь последовательно. Вероятность перегореть для любой лампочки при повышении напряжения в сети равна 0,1. Определить вероятность разрыва цепи при повышении напряжения в сети.

5.6.Вероятность того, что покупателю потребуется обувь 43-го размера, равна 0,4. В обувной магазин вошли трое покупателей. Найти функцию распределения случайной величины Х – числа тех покупателей, которым потребовалась обувь 43-го размера. Вычислить Р(х ≥2).

5.7.В некотором цехе брак составляет 5% всех изделий. Составить закон распределения числа бракованных изделий из 6 наудачу взятых изделий. Найти математическое ожидание и дисперсию этой случайной величины.

5.8.Изделия некоторого производства содержат 5% брака. Взято 5 изделий. Построить ряд распределения числа бракованных изделий и среднее квадратичное отклонение этой случайной величины.

5.9.В течение года может обанкротиться примерно один банк из 50. Определить, какова вероятность того, что из 200 банков обанкротятся: а) не более двух банков, б) не менее восьми.

5.10.Акционерное общество выпустило очередной пакет акций по номинальной стоимости за акцию 100000 и 10000 рублей. Причем в пакете 80% акций по цене 100000 и 20% по цене 10000 рублей. Какова вероятность того, что из наудачу взятых по схеме возвратной выборки восьми акций пять окажутся по цене 100000 рублей?

5.11.Вероятность того, что покупатель войдет в магазин в течение часа, равна 0,005. Магазин обслуживает 600 покупателей. Какова вероятность того, что в течение часа войдет 5 покупателей?

5.12.Из 20 изделий цеха 25% изделия высшего сорта. ОТК проверяет 8 изделий. Какова вероятность того, что из них 6 изделий будут высшего сорта?

5.13.Банк в течение дня принимает 200 денежных вкладов от населения. Определить с тремя десятичными знаками вероятность того, что среди них окажется 100 – валютные, если вероятность принятия вклада в расчетных билетах РБ равна 0,515.

5.14.Работники коммерческого банка производят 2 вида операций: депозитные и кредитные счета. Проверка обнаружила, что вероятности допущения ошибок при оформлении депозитных и кредитных счетов соответственно равны 0,1 и 0,15. Найти вероятность следующих исходов: а) в пяти проверенных депозитных счетах обнаружено не менее двух неправильных; б) в трех проверенных кредитных счетах обнаружены 2 ошибки.

5.15.Какое минимальное число п испытаний нужно провести, чтобы с вероятностью не меньшей, чем 0,95, можно было бы ожидать наступление события А хотя бы один раз, если вероятность события А в одном испытании равна 0,3.

Решение. Наступление события А хотя бы один раз в п испытаниях обозначает, что событие А наступит или один раз или два раза или… во всех испытаниях. Поэтому проще вычислить вероятность противоположного события 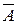, состоящего в том, что событие А не наступит ни в одном испытании. Так как испытания независимы, то по теореме умножения для независимых событий будем иметь: 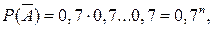где 0,7=1– 0,3.

Тогда вероятность события А вычисляется по формуле: 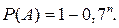Потребуем, чтобы эта вероятность была не меньше, чем 0,95: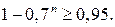

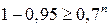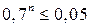Решив это неравенство последовательно относительно п, получим: , или 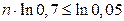, или , или 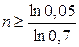, так как .

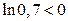Отсюда заключаем, что минимальное число испытаний определяется формулой 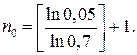Вычислив ln 0,05≈ –2,996; ln 0,7= –0,357, получим п₀≈ 9.

Ответ: максимальное число испытаний равно 9.

5.16.На контроль поступила партия деталей из цеха. Известно, что 5% всех изделий не удовлетворяют стандарту. Сколько нужно испытать деталей, чтобы с вероятностью 0,95 обнаружить хотя бы одну нестандартную деталь?

5.17.Всхожесть семян составляет в среднем 90%. Найти наивероятнейшее число всхожих семян среди 20 семян.

Решение. Воспользуемся формулой (5.2), так как число всхожих семян подчиняется биномиальному закону распределения. Подставив 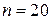, , 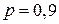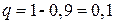получим 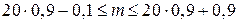или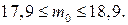

Из последнего неравенства следует, что т₀=18.

5.18.Из практики известно, что в среднем 3% отчетов представляемых фирмами в налоговую инспекцию имеет ошибки. Определить наивероятнейшее число отчетов, не содержащих ошибок, среди 100 сданных отчетов.

5.19.На предприятии работает 1000 рабочих. Какова вероятность того, что 1 января является днем рождения одновременно т рабочих данного предприятия? Вычислить вероятность для значений m равных 0, 1, 5.

Решение. Рассмотрим случайную величину Х – число рабочих, родившихся 1 января. Эта случайная величина 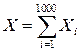, где 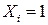, если рабочий родился 1 января и X_i =0, если рабочий родился не 1 января. Вероятность события А=Х{рабочий родился 1 января} равна 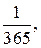т.е. небольшая, а число п достаточно большое, то можно считать, что случайная величина Х подчиняется закону распределения Пуассона с параметром 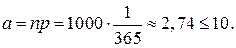Поэтому для вычисления искомых вероятностей применим формулу (5.3):

если т=0, то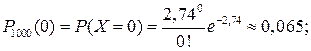

если т=1, то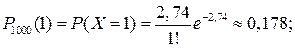

если т=5, то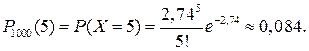

5.20.Число регистрируемых заявок в телеателье случайно и образует пуассоновскую случайную величину Х со средним значением 500 заявок в день каждая регистрируемая заявка может быть выполнена с вероятностью 0,99. Описать закон распределения числа не выполненных заявок, регистрируемых диспетчером. Вычислить М(Х) и D(Х).

Решение. Рассмотрим случайную величину Х – число не выполненных заявок за день. Так как число заявок п=500 велико, а вероятность события А{заявка не выполнена} мала Р(А)=0,01, то закон распределения случайной величины Х задается в виде:

xi				…
pi				…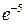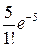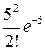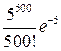

где а=пр=500∙0,01=5.

Математическое ожидание равно дисперсии для случайной величины Х, подчиняющейся закону распределения Пуассона, т.е.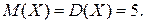

5.21.Установлено, что численность обрывов нити за некоторой промежуток времени следует закону Пуассона. Прядильщица обслуживает 800 веретен. Наблюдения показали, что в течение 1 минуты в среднем происходит 5 обрывов. Определить вероятность того, что в течение 1 минуты произойдет: а) 5 обрывов; б) не менее пяти обрывов.

5.22.Среднее число вызовов, поступающих на АТС в минуту равно 120. Найти вероятность следующих событий:

А={за две секунды на АТС не поступит ни одного вызова};

В={за две секунды на АТС поступит менее двух вызовов}.

5.23.Корректура в 500 страниц содержит 1300 опечаток. Найти наиболее вероятное число опечаток на одной станице текста и вероятность этого числа.

5.24.При испытании легированной стали на содержание углерода вероятность того, что в случайно взятой пробе процент углерода превысит допустимый уровень, равна 0,01. Считая применимым закон Пуассона, вычислить, сколько в среднем необходимо испытать образцов, чтобы с вероятностью р=0,95 указанный эффект наблюдался по крайней мере 1 раз.

5.25.Отдел по обмену валюты сбербанка производит в течение рабочего дня 300 операций. Вероятность совершить ошибку при обмене валюты равна 0,01. Найти вероятности следующих исходов: а) не более трех операций из 300 будет произведено с ошибками; б) пять операций из 300 будет произведено с ошибками.

5.26.Вероятность того, что к концу года акционерное общество банкротится, равна 0,004. Найти вероятность того, что из 1000 акционерных обществ к концу года обанкротится не более пяти.

5.27.Вероятность того, что стеклянное изделие повредится при перевозке по железной дороге, равна 0,001. Какова вероятность того, что из 1000 стеклянных изделий при перевозке повредится: а) три изделия? б) больше трех изделий?

5.28.В тесто, подготовленное для выпечки 500 булочек, засыпают 5000 изюминок и тщательно перемешивают. Какова вероятность того, что в случайно выбранной булочке будет: а) 10 изюминок? б) больше 10 изюминок?

5.29.Производится ряд попыток реализации некоторого товара по фиксированной цене r₀. Каждая попытка длительностью 7 часов заканчивается реализацией товара по цене r₀ независимо от других попыток с вероятностью р=0,095. Описать распределение общего времени Т, которое требуется для реализации некоторого товара. Вычислить функцию распределения, математическое ожидание и среднее квадратическое отклонение случайной величины Т – времени, необходимого для реализации товара.

Решение. Введем случайную величину Х – число попыток реализовать товар по фиксированной цене r₀. Эта случайная величина распределена по геометрическому закону распределения. Общее время Т, необходимое для реализации товара, связано со случайной величиной Х по формуле Т–tX, где t=7ч и имеет распределение вида:

Ti	t∙1=7	t∙2=14	t∙3=21	…	t∙т=7т	…
P(X=xi)	р=0,95	q∙p=0,05∙0,95=0,0475	q2∙p=0,052∙0,95	…	qn-1∙p=0,05m∙0,95	…

Функция распределения общего времени Т, необходимого для реализации товара:

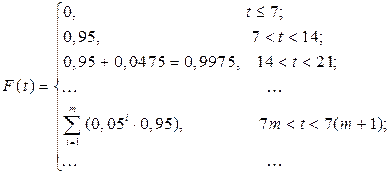
Математическое ожидание и среднее квадратическое отклонение случайной величины Т равны:

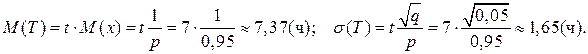
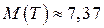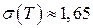Ответ: ч.; ч.

5.30.Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,8. Стрелку выдаются патроны до тех пор, пока он не промахнется. Требуется: а) составить закон распределения дискретной случайной величины Х – числа патронов, выданных стрелку; б) найти наивероятнейшее число выданных стрелку патронов.

5.31.Экзаменатор задает студенту дополнительные вопросы. Вероятность того, что студент ответит на любой заданный вопрос, равна 0,9. Преподаватель прекращает экзамен, как только студент не отвечает на заданный вопрос. Требуется: а) составить закон распределения дискретной случайной величины Х – числа дополнительных вопросов, которые задаст преподаватель студенту; б) найти наивероятнейшее число заданных студенту дополнительных вопросов.

5.32.Из ящика, содержащего 4 изделия, содержащих скрытый дефект, и 6 стандартных изделий, случайным образом и без возвращения извлекают три изделия. Описать закон распределения случайной величины Х – число изделий в выборке, содержащих скрытый дефект. Вычислить функцию распределения, математическое ожидание и дисперсию случайной величины Х.

Решение: Из 10 изделий 4 изделия содержат скрытый дефект и 6 стандартных изделий. Следовательно, случайная величина Х – число изделий в выборке, содержащих скрытый дефект, подчиняется гипергеометрическому закону распределения. Вероятность того, что случайная величина Х может принимать значение, равное т=0,1,2,3, вычисляется на основании классического определения вероятности, т.е. по формуле:

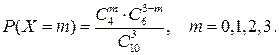
Закон распределения случайной величины Х задается в виде:

xi
P(X=xi)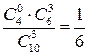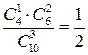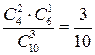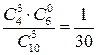

Функция распределения:

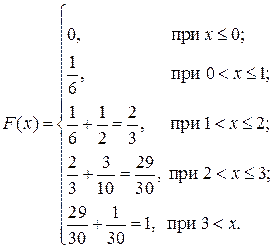
Числовые характеристики случайной величины, распределенной по гипергеометрическому закону распределения равны: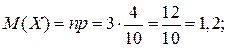

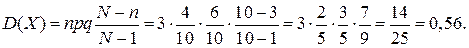
Ответ: М(Х)=1,2; D(X)=0,56.

5.33.На станции технического обслуживания устраняется один дефект автомобилей. На одну рабочую смену требуется 5 однотипных деталей. Было закуплено 16 деталей, из которых 12 не имеют дефектов. Мастер на складе получает 6 деталей, которые отбираются наудачу, на одну рабочую смену (одну деталь «про запас», учитывая наличие бракованных). Найти вероятность того, что за смену будут устранены все дефекты.

5.34.На контроль поступила партия деталей. Известно, что для данных изделий брак составляет 7,5%. Сколько нужно испытать деталей, чтобы с вероятностью не менее 0,95 обнаружить хотя бы одну нестандартную деталь?

5.35.На факультете обучается 500 студентов, 20 из которых систематически занимается научной работой. На конференцию случайным образом отбирают 5 студентов. Описать закон распределения случайной величины Х – число студентов в выборке, которые занимаются научной работой. Вычислить функцию распределения, математическое ожидание и среднее квадратическое отклонение случайной величины Х. Построить график функции распределения.