Алгоритм решения показательных неравенств

Алгоритм	Образец решения
1. Выбираем основание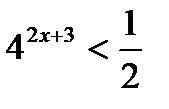
2. Приводим обе части неравенства к одному основанию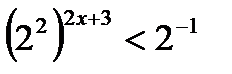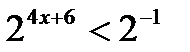
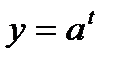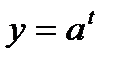3. Если a > 1,то функция возрастающая, значит, знакнеравенства сохраняем;   Если 0 < a < 1,то функция убывающая, значит, знак неравенства меняем.	так как а = 2 > 1, то функция 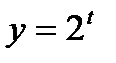возрастающая, значит,
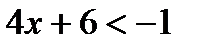4. Решаем полученное неравенство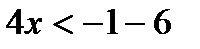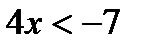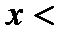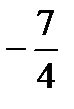
Решение отмечаем на числовой оси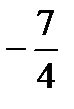
5. Ответ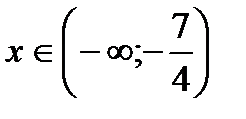

Логарифмы

Определение логарифма

, где

Основное логарифмическое тождество

Свойства логарифмов

1.

2.

3.

4.

5.

6.

7.

8.

9.

Функции и графики функций

Степенные функции с целым показателем

График	График	n-положительное, чётное, натуральное число
n=0	n=1
График	График	График
n-положительное, нечётное, натуральное число	n-отрицательное, нечётное, целое число	n-отрицательное, чётное, целое число

Степенные функции с дробным показателем

Функции вида

n-чётное	n-нечётное

Показательная функция

основание а>1, функция возрастающая	основание 0<а<1, функция убывающая

Логарифмическая функция

основание а>1, функция возрастающая	основание 0<а<1, функция убывающая

Преобразование графика функции y = f(x)

f(x)+A	Параллельный перенос графика по оси у на А единиц : вверх, если А > 0, вниз, если А < 0.
f(x-B)	Параллельный перенос графика вдоль оси х на В единиц : вправо, если В > 0, влево, если В < 0. (подсказка: решить уравнение х - В = 0, где х = В, затем определять знак числа В и направление перенос)
C ∙ f(x)	Умножение каждой ординаты у графика функции на число С
f(D∙x)	Деление каждой абсциссы х графика функции на число D
- f(x)	«Зеркальное» отображение графика функции относительно оси х (подсказка: смотри пункт 3 )

Первообразная и интеграл

Таблица первообразных

– функция	– общий вид первообразных функции

Неопределенный интеграл .

Свойства неопределенного интеграла

1.

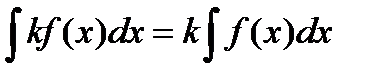
2.

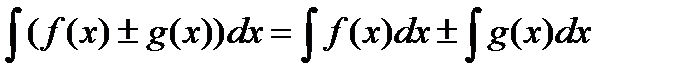
3.

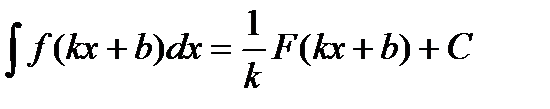
Определенный интеграл .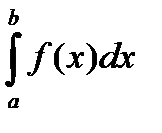

Формула вычисления площади криволинейной трапеции (формула Ньютона-Лейбница)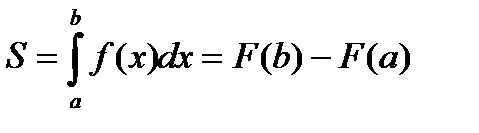

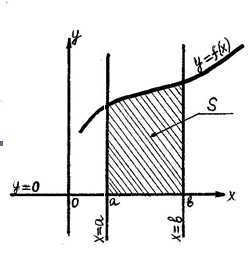Теория вероятностей и

Математическая статистика

Факториал .

Перестановки – комбинация из n элементов по n элементов, где отличается только порядок их следования (состав не важен).

.

Размещения– из n элементов выбирается k элементов, которые отличаются хотя бы одним элементом или порядком их следования (важен порядок следования и состав).

– с повторениями; – без повторений.

Сочетания – число комбинаций из n элементов по k элементов, которые отличаются хотя бы одним элементом, порядок не важен, важен состав.

Бином Ньютона

член разложения бинома Ньютона

Треугольник Паскаля

Вероятность случайного события , где m – количество благоприятных исходов события А, n – количество всевозможных исходов события А.

Сумма биномиальных коэффициентов разложения бинома

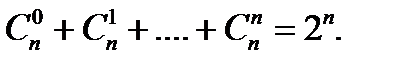
Теорема Бернулли

Пусть – вероятность наступления ровно k «успехов» в n независимых повторениях одного и того же испытания. Тогда,

,

где p – вероятность «успеха», а – вероятность «неудачи» в отдельном испытании.

Уравнения и неравенства

1. Показательное уравнение где равносильно уравнению

2. Логарифмическое уравнение ,где равносильно системе .

3. Показательное неравенство вида равносильно:

а) если то

б) то

4. Логарифмическое неравенство вида равносильно системе неравенств:

а) если то ;

б) то .

5. Иррациональное неравенство вида:

а) равносильно системе неравенств ;

б) равносильно совокупности систем неравенств

Геометрия

Многогранники

	Боковая поверхность	Полная поверхность	Объём
Прямая призма	где периметр основания, Н – высота призмы		где площадь основания, Н – высота призмы
Параллелепипед прямоугольный
Куб
Правильная пирамида	где периметр основания, l – апофема		где площадь основания, Н – высота пирамиды

Тела вращения
	Боковая поверхность	Полная поверхность	Объём
Цилиндр R H	где R – радиус основания, Н – высота цилиндра	где
Конус	где R – радиус основания, l – образующая конуса	где	где H – высота конуса
Шар	------

Решение квадратного уравнения	D>0 – два корня: D<0 – нет корней D=0 – один корень:
Разложение квадратного трехчлена на множители
Четность, нечетность функций	1. 2. f(–x)=f(x) – четная функция, симметрия относительно оси OY 3. f(– x)= – f(x) – нечетная функция, симметрия относительно начала координат
Формулы сокращенного умножения
	разность квадратов
	квадрат разности
	квадрат суммы
	куб суммы
	куб разности
	разность кубов
	сумма кубов

Теорема Пифагора B     а с C A b c2=a2+b2

Соотношение сторон и углов прямоугольного треугольника

Таблица квадратов натуральных чисел от 10 до 99

десятки	единицы

Список литературы

1. Башмаков М.И. Математика (базовый уровень): учебник для 10 класса: среднее общее образование / М.И.Башмаков. – М.: Издательский центр «Академия», 2014. – 304 с.

2. Башмаков М.И. Математика (базовый уровень): учебник для 11 класса: среднее общее образование / М.И.Башмаков. – М.: Издательский центр «Академия», 2014. – 320 с.

3. Башмаков М.И. Математика: учебник для учреждений нач. и сред. проф. образования / М.И.Башмаков. – 5-е изд., испр. – М.: Издательский центр «Академия», 2012. – 256 с.

4. Пехлецкий И.Д. Математика: учебник для студентов образовательных учреждений среднего профессионального образования – М.: Академия, 2012. – 304 с.