Теория вероятностей и математическая статистика

Теория вероятностей – это математическая наука, которая изучает свойства массовых случайных событий или явлений, способных многократно повторяться при воспроизведении определенного комплекса условий.

Предметом теории вероятностей является математический анализ случайных явлений, которые характеризуются тем, что наблюдение над ними не всегда приводит к одним и тем же исходам и что они обладают некоторой регулярностью.

§ 1. Основные понятия и определения теории вероятностей.

Теория вероятностей, как и всякая наука, содержит ряд основных понятий, на которых она базируется.

Испытанием будем называть эксперимент, опыт, наблюдение.

Результат испытания назовем событием. События будем обозначать большими буквами латинского алфавита.

События, которые в результате могут происходить или не происходить называются случайными.

Определение. Если при воспроизведении определенного комплекса условий событие обязательно наступит, то оно называется достоверным, если событие никогда не наступит, то оно называется невозможным.

Например, невозможным является событие, состоящее в извлечении наугад скальпеля из коробки, содержащей только пинцеты.

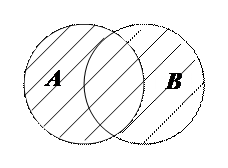
Определение. Два события называются несовместными, если появление одного из них исключает появления другого в одном и том же испытании.

Например, произведено испытание - брошена монета. В результате произошло событие - выпал герб. Появление герба исключает появление решки. События «выпал герб» и «выпала решка» - несовместные.
Произведено испытание - психолог предъявил обследуемому вопрос. По условиям испытания обследуемый может дать только один из двух ответов: «да» или «нет». Отсюда, результатом испытания может быть только одно из двух несовместных событий.

Определение. Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

Например, если первое событие состоит в выпадение цифры 2 при однократном бросании игрального кубика, а второе событие – в выпадении четного числа очков, то эти два события – совместные, так как цифра 2 является четной.

Определение. События называются независимыми, если вероятность появления одного события не влияет на вероятность появления другого. В противном случае события называются зависимыми.

Определение. Противоположным событию 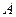называется событие 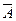, состоящее в том, что событие 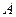не произошло.

Пример. Бросаем один раз игральную кость. Событие 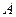- выпадение четного числа очков, тогда событие 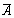- выпадение нечетного числа очков.

Элементы комбинаторики.

Комбинаторика – это наука о расположении элементов в определенном порядке и о подсчете числа способов такого расположения.

Существуют два основных правила комбинаторики:

1. Правило « суммы»: Если элемент 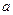можно выбрать 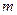способами, а элемент 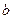– 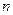способами, то элемент «либо 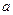, либо 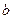» можно выбрать 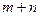способами.

2. Правило « произведения»: Если элемент 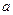можно выбрать 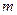способами, а элемент 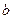– 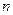способами, то элемент 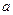« и и 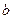» можно выбрать 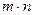способами.

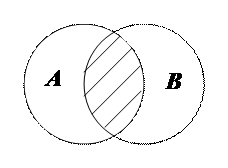
Существует 3 типа комбинаций:

1. Перестановки – это такой тип комбинаций, который связан с нумерацией или перестановкой элементов.

Теорема 1. Число перестановок без повторений вычисляется по формуле

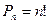
Теорема 2. Число перестановок с повторениями вычисляется по формуле

,

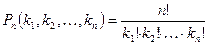где 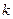– число повторов.

Пример.Сколько слов можно получить, переставляя буквы в слове « математика»?

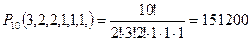
2. Сочетания – это такой тип комбинаций, который связан с выбором элементов.

Теорема 3. Число сочетаний без повторений вычисляется по формуле

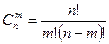
Пример.Сколько существует способов выбора 3 студентов на конференцию из 20?

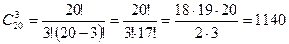
Теорема 4. Число сочетаний с повторениями вычисляется по формуле

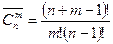
Пример.В буфете имеются 4 типа пирожных. Сколькими способами можно купить 7 пирожных?

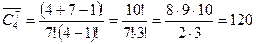
3. Размещения – это такой тип комбинаций, который связан и с выбором и перестановкой элементов.

Теорема 5.Число размещений без повторений вычисляется по формуле

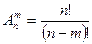
Пример .Сколькими способами можно выбрать старосту и профорга, если в группе 8 человек?

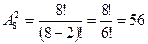
Теорема 6. Число размещений с повторениями вычисляется по формуле

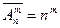
Пример.Сколько существует пятизначных номеров телефонов?