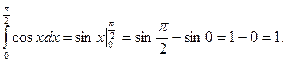Понятие определенного интеграла

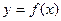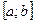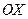Определение. Фигура, ограниченная кривой , отрезком оси , прямыми 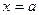и 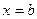называется криволинейной трапецией.

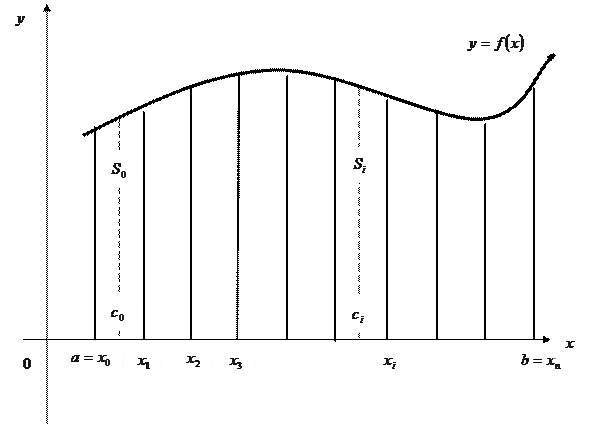
Для вычисления площади 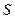этой криволинейной трапеции разобьем отрезок 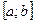произвольным образом на 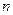частей и обозначим точки деления 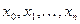, причем 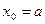, а .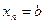

Восстановим из этих точек перпендикуляры до пересечения с кривой, получим значения функции в этих точках: 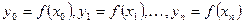. В результате этого площадь криволинейной трапеции окажется разбитой на сумму площадей элементарных криволинейных трапеций. В отрезках 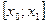, , 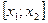, , 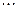, 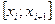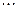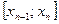возьмем совершенно произвольно точки 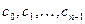и восстановим перпендикуляры из этих точек до пересечения с кривой 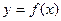. Получим значения .

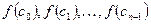Далее построим ступенчатую фигуру, состоящую из прямоугольников, имеющих своими основаниями отрезки 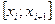, а высотами 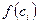. Эта фигура ограниченна ломаной линией. Площадь 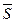этой ступенчатой фигуры можно считать приближенным значением площади 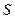заданной криволинейной трапеции, причем тем более точной, чем больше 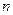и чем меньше длины отрезков .

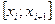Площадь 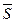равна сумме площадей прямоугольников, построенных на отрезках: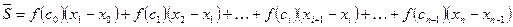

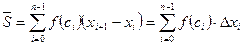(1)

Если теперь в (1) неограниченно увеличить число 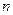так чтобы длина наибольшего из отрезков стремилась к нулю, т. е. 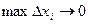, то площадь 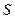криволинейной трапеции будет равна пределу суммы (1).

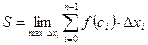(2)

Сумма (1) называется интегральной суммой.

Определение. Если существует конечный предел интегральной суммы при условии, что 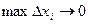, то этот предел называют определенным интегралом от функции 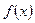на 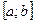и обозначают 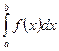.Т. об. По определению

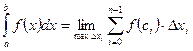
Числа 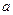и 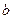называются нижним и верхним пределами интегрирования соответственно. Определенный интеграл выражает число.

Процесс вычисления определенного интеграла называют интегрированием. Функция 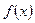называется подынтегральной функцией, а переменная – переменная интегрирования.

Определение. Функция 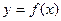называется интегрируемой на отрезке 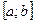, если на этом отрезке существует определенный интеграл от этой функции.

Основные свойства определенного интеграла

1. Определенный интеграл от алгебраической суммы нескольких функций, интегрируемых на отрезке 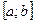, равен алгебраической сумме определенных интегралов этих функций на данном отрезке:

.

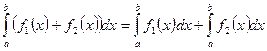2. определенный интеграл от произведения постоянного множителя 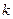на интегрируемую на отрезке 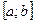функцию 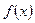равен произведению этого множителя на определенный интеграл от этой функции:

.

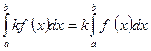3. При перемене местами пределов интегрирования величина определенного интеграла изменяется на противоположную:

.

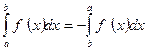4. Если отрезок интегрирования 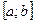разбит точкой 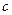на два отрезка, то определенный интеграл от функции 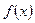на отрезке 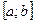равен сумме определенных интегралов от этой функции на каждом из этих отрезков:

.

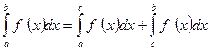Формула Ньютона – Лейбница

Теорема. Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятой при верхнем и нижнем пределах интегрирования.

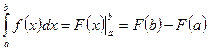
Данная формула называется формулой Ньютона – Лейбница и дает практически удобный метод вычисления определенного интеграла в том случае, когда известна первообразная подынтегральной функции.

Основными методами интегрирования определенного интеграла являются те же, что и для неопределенного.

Пример. Вычислить определенный интеграл

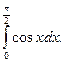
Решение.