Метод логарифмического дифференцирования.
Во многих случаях оказывается целесообразным прежде чем дифференцировать заданную функцию, взять ее логарифм, определить затем производную от этого логарифма, а затем найти производную заданной функции. Такой прием называется методом логарифмического дифференцирования. Этот метод позволяет легко найти производную от сложной функции вида 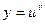 , где
, где  и
и  есть функции зависящие от
есть функции зависящие от  .
.
Пусть дана функция 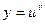 .
.
1. 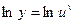 4.
4. 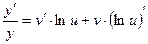
2. 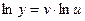 5.
5. 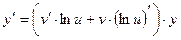
3. 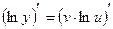 6.
6. 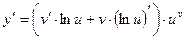
Пример. Найти производную функции 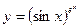 .
.
Применим метод логарифмического дифференцирования.
1. 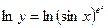 4.
4. 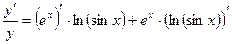
2. 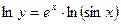 5.
5. 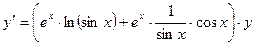
3. 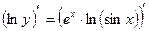 6.
6. 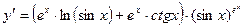
Дифференцирование логарифмической функции.
Дифференцирование логарифмической функции рассмотрим на примере.
Пусть дана функция 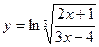 . Выполним некоторые преобразования, пользуясь общими правилами логарифмирования и свойствами логарифмов:
. Выполним некоторые преобразования, пользуясь общими правилами логарифмирования и свойствами логарифмов:
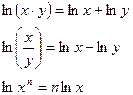
Получим 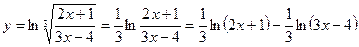 .
.
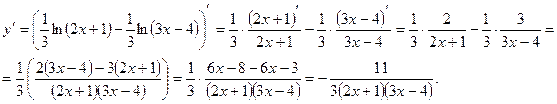
Производные высших порядков
Производную 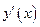 называют еще первой производной, или производной первого порядка, функции в отличие от так называемых производных высших порядков.
называют еще первой производной, или производной первого порядка, функции в отличие от так называемых производных высших порядков.
Производная 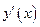 функции
функции 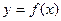 в общем случае представляет собой некоторую новую функцию, которая в свою очередь тоже может быть дифференцируемой. Следовательно, можно найти производную и этой функции, представляющую собой производную от производной исходной функции и называемую второй производной, или производной второго порядка, исходной функции. Производную второго порядка принято обозначать
в общем случае представляет собой некоторую новую функцию, которая в свою очередь тоже может быть дифференцируемой. Следовательно, можно найти производную и этой функции, представляющую собой производную от производной исходной функции и называемую второй производной, или производной второго порядка, исходной функции. Производную второго порядка принято обозначать 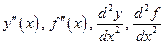 .
.
Производную от производной второго порядка, если она существует, называют третьей производной функции , или производной третьего порядка, и обозначают 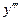 или
или 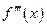 и т. д.
и т. д.
Определение. Производные порядков выше первого называются производными высших порядков.
При этом производная 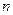 -го порядка определяется как производная от производной предыдущего порядка, т. е.
-го порядка определяется как производная от производной предыдущего порядка, т. е.
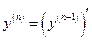 .
.
Пример. Найти вторую производную функции 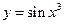 .
.
Найдем сначала первую производную 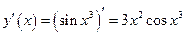 .
.
Найдем вторую производную
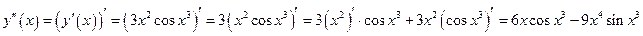
Применение производных при исследовании функций
Возможность применения производных при исследовании функций основана на связи, существующей между производными функций и некоторыми особенностями графиков этих функций.
Связь производной функции с наличием промежутков ее возрастания и убывания
Как мы уже говорили, функция 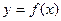 называется возрастающей на интервале
называется возрастающей на интервале 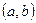 , если для любых двух значений
, если для любых двух значений 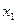 и
и 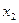 , принадлежащих этому интервалу и удовлетворяющих неравенству
, принадлежащих этому интервалу и удовлетворяющих неравенству 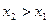 , выполняется неравенство
, выполняется неравенство 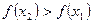 , и убывающей, если при этих же условиях выполняется неравенство
, и убывающей, если при этих же условиях выполняется неравенство 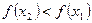 .
.
Теорема 1.
1) Если функция 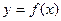 дифференцируема и возрастает на интервале
дифференцируема и возрастает на интервале 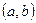 , то производная этой функции не отрицательна
, то производная этой функции не отрицательна 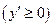 во всех точках данного интервала.
во всех точках данного интервала.
2) Если функция 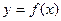 дифференцируема и убывает на интервале
дифференцируема и убывает на интервале 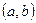 , то производная этой функции не положительна
, то производная этой функции не положительна 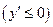 во всех точках данного интервала.
во всех точках данного интервала.
Эту теорему называют теоремой о необходимых признаках возрастания и убывания функции, поскольку в ней указывается, какой должна быть производная дифференцируемой функции на интервале в случаях соответственно возрастания и убывания функции.
Необходимо помнить, что неотрицательность производной является лишь необходимым, но не достаточным условием для утверждения о возрастании функции, точно так же, как неположительность производной не является достаточным условием для утверждения о ее убывании.
Теорема 2.
1) Если производная функции положительна 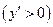 на интервале
на интервале 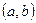 ,то функция возрастает на этом интервале.
,то функция возрастает на этом интервале.
2) Если производная функции отрицательна 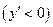 на интервале
на интервале 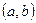 ,то функция убывает на этом интервале.
,то функция убывает на этом интервале.
Эту теорему называют теоремой о достаточных признаках возрастания и убывания функции, поскольку в ней указывается, при каком знаке производной на интервале дифференцируемая функция возрастает и при каком – убывает.
