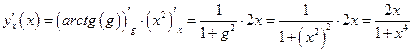Геометрический смысл производной
Производная функции в точке имеет достаточно простую геометрическую интерпретацию.
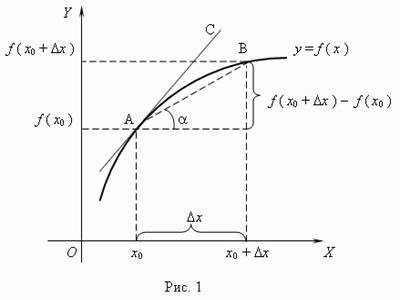
Пусть дана кривая 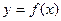 . Возьмем на ней точку
. Возьмем на ней точку 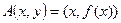 и дадим аргументу
и дадим аргументу  приращение
приращение 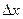 . Тогда получим новый аргумент
. Тогда получим новый аргумент 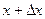 и новое значение функции
и новое значение функции 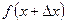 , т. е. мы получили новую точку на кривой и обозначим её через
, т. е. мы получили новую точку на кривой и обозначим её через 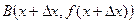 . Проведем секущую
. Проведем секущую 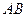 и обозначим угол наклона секущей к оси
и обозначим угол наклона секущей к оси 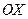 через
через 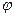 . Рассмотрим прямоугольный треугольник
. Рассмотрим прямоугольный треугольник 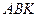 :
:
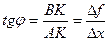 .
.
При 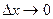 точка
точка 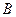 перемещается вдоль кривой, приближаясь к точке
перемещается вдоль кривой, приближаясь к точке 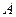 . Секущая
. Секущая 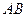 поворачивается вокруг точки
поворачивается вокруг точки 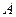 и величина угла
и величина угла 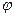 изменяется. При приближении секущей
изменяется. При приближении секущей 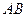 к касательной
к касательной 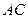 угол
угол 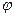 приближается к углу
приближается к углу 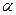 .
.
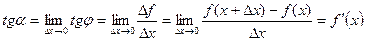 .
.
Так как в математике величину угла наклона касательной, проведенной к графику функции называют угловым коэффициентом касательной, то из полученной формулы следует, что угловой коэффициент касательной, проведенной к графику дифференцируемой функции в некоторой точке, численно равен производной функции в данной точке.
Это и есть геометрический смысл производной.
Уравнение касательной: 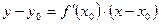 .
.
Уравнение нормали: 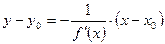 .
.
Производные основных элементарных функций
1. 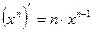 1.
1. 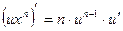
2. 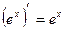 2.
2. 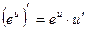
3. 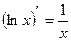 3.
3. 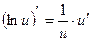
4. 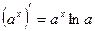 4.
4. 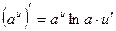
5. 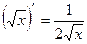 5.
5. 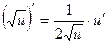
6. 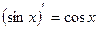 6.
6. 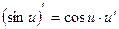
7. 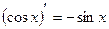 7.
7. 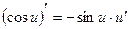
8. 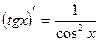 8.
8. 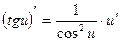
9. 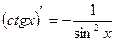 9.
9. 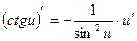
10. 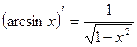 10.
10. 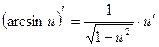
11. 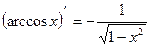 11.
11. 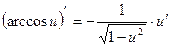
12. 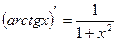 12.
12. 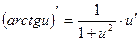
13. 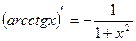 13.
13. 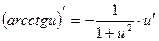
Основные правила дифференцирования функций
Правило 1. Производная константы (постоянной величины) равна нулю 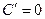 .
.
Правило 2. Производная аргумента равна единице 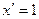 .
.
Правило 3. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций 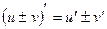 .
.
Пример. 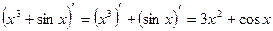
Правило 4. Производная произведения двух дифференцируемых функций равна сумме произведений производной первой функции на вторую и первой функции на производную второй 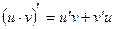 .
.
Пример. 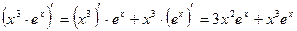
Следствие из правила 4. Производная произведения постоянного множителя на дифференцируемую функцию равна произведению этого множителя на производную данной функции 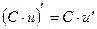 .
.
Пример. 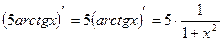
Правило 5. Производная частного двух дифференцируемых функций ( при условии, что знаменатель не обращается в нуль) равна дроби, числитель которой представляет собой разность между произведением производной первой функции на вторую и произведением первой функции на производную второй, а знаменатель равен квадрату второй функции 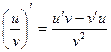 .
.
Пример. 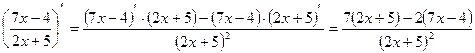
Производная сложной функции
Теорема. Если функция 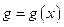 определена и дифференцируема на интервале
определена и дифференцируема на интервале 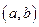 , причем областью ее значений является интервал
, причем областью ее значений является интервал 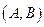 , а функция
, а функция 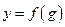 определена и дифференцируема на интервале
определена и дифференцируема на интервале 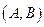 , то производная сложной функции
, то производная сложной функции 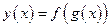 существует и равна произведению производной внешней функции по ее аргументу
существует и равна произведению производной внешней функции по ее аргументу 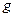 на производную внутренней функции
на производную внутренней функции 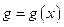 по ее аргументу
по ее аргументу  :
:
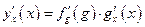 ,
,
Причем в этой формуле при обозначении производных под штрихом в виде индексов указаны переменные, по которым ведется дифференцирование.
Пример.  Найти производную сложной функции
Найти производную сложной функции 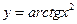 .
.
Т. к. данная функция является сложной, то введем в рассмотрение внутреннюю функцию  и внешнюю функцию
и внешнюю функцию 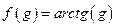 . С учетом этих обозначений исходная функция может быть представлена в виде
. С учетом этих обозначений исходная функция может быть представлена в виде 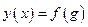 и для нахождения ее производной применяем формулу
и для нахождения ее производной применяем формулу 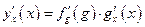 :
: