Звуковые колебания в жидкости и газе

Как мы уже говорили, что движение газа или сжимаемой жидкости описывается одними и теми же уравнениями. В частности это имеет место при описании звуковых колебаний или звуковых волн в этих средах. Звуковыми волнами называют колебательные движения в сплошной среде с малыми амплитудами, что соответствует экспериментально установленному факту. В каждой точке среды, в частности сжимаемой жидкости или газа, при распространении звуковых волн происходит попеременное сжатие и расширение.

Для простоты мы будем рассматривать распространение звука в покоящейся жидкости или газе (в дальнейшем мы будем говорить о сжимаемой жидкости, имея в виду и газ) в отсутствии внешних сил. В этом случае, в силу малости колебаний в звуковой волне скорость жидкости будет мала и в уравнении Эйлера (14') можно пренебречь членами, содержащими компоненту скорости, умноженную на саму скорость, т.е. 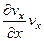и т. д. По той же причине относительные изменения плотности и давления также будут малы, что позволяет нам представить плотность и давление следующим образом

(37)

где p₀ и ρ₀ – постоянные давление и плотность покоящейся жидкости, а 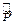и 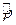- их изменения в звуковой волне, причем 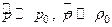. Величину 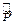называют звуковым давлением.

Подставляя в уравнение неразрывности (2) соотношения (37) и пренебрегая малыми величинами второго порядка, мы получим

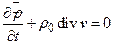
или, вводя величину

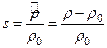
будем иметь

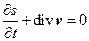(38)

Уравнения Эйлера (14') в отсутствии внешних сил и при тех же предположениях малости сведутся к уравнениям

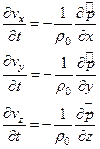(39)

или в векторной форме

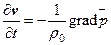(39')

Уравнения (38) и (39) содержат пять неизвестных v_x, v_y, v_z, s и 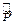. Одну из них, а именно 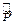, мы можем исключить, выразив её через s с помощью уравнения сосотояния (25), записанного в том же приближении малости

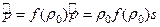(40)

Величина 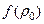– постоянная и кроме того, положительная, поскольку в жидкостях и газах при постоянной энтропии с ростом плотности давление возрастает. В силу этого можно обозначить 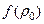через 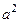и переписать (40) в виде

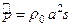
.Подставляя теперь это выражение в (39'), получим

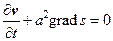(41)

Применяя к этому уравнению операцию дивергенции, мы получим

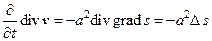(42)

Принимая во внимание уравнение (38), окончательно получим

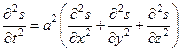(43)

Таким образом, величина s подчиняется волновому уравнению. Можно показать, что и для давления p и для скоростиvможно получить уравнения такого же типа.

Предположим теперь, что в начальный момент скорость обладала потенциалом 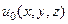, т.е.

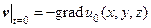(44)

Тогда интегрируя уравнение (41), мы сможем написать

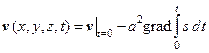(45)

Учитывая далее (44), получим

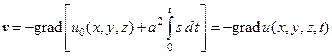(46)

Это означает, что потенциал скоростей существует в любой момент времени t:

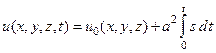(47)

Можно показать, что потенциал скоростей удовлетворяет волновому уравнению. Действительно, дифференцируя полученное выражение (47) два раза по t, мы получим

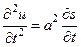(48)

С другой стороны, подставляя выражение (46) в уравнение(41), будем иметь

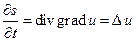(49)

Сравнивая теперь (48) и (49) мы получим

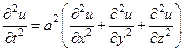(50)

Заметим, что знание потенциала скоростей достаточно для определения величин, характеризующих процесс движения жидкости в звуковой волне. В самом деле, по определению

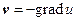
Из (48) следует, что

,

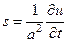а из этого выражения и выражения (39') следует, что

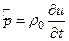
Если нам в начальный момент времени задано распределение скоростей и величина s, то это позволяет сформулировать начальные условия для потенциала u в следующем виде

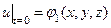
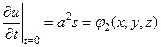
Если при этом граница области S непроницаема, то нормальная составляющая скорости на границе должна быть равна нулю, что дает граничное условие для u в виде

.

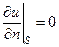Литература

1. Смирнов В. И. Курс высшей математики. Том II – IV. М.: Наука, 1974-1981.

2. Кошляков Н. С., Глинер Э. Б., Смирнов М. М. Дифференциальные уравнения математической физики. М.: Высшая школа, 1970.

3. Тихонов А. Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1966.

4. Михлин С. Г. Линейные уравнения в частных производных. М.: Высшая школа, 1977.

5. Соболев С. Л. Уравнения математической физики. М.: Наука, 1966.

6. Владимиров В. С. М.: Уравнения математической физики. М.: Наука, 1971.

7. Арфкен Г. Математические методы в физике. М.: Атомиздат, 1970.

8. Фарлоу С. Уравнения с частными производными для научных работников и инженеров. М.: Мир 1985.

[1]⁾ Кузютин В. Ф., Зенкевич Н. А., Еремеев В. В. Геометрия. СПб.: Лань, 2003 г. 416 с. (с. 300–301)