Единственность и устойчивость решения задачи Дирихле.

В этой задаче граничные условия формулируются следующим образом

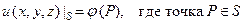(69)

Единственность решения будем доказывать от противного. Предположим, что задача имеет два решения u₁ и u₂. Тогда разность решений 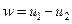будет представлять собой гармоническую функцию в области D, обращающуюся в нуль на её границе. Для ограниченной области можно непосредственно применить теорему о максимуме и минимуме. Согласно этой теореме внутри области D гармоническая функция w не может иметь значений больше или меньше своего граничного значения, равного нулю. Поэтому она равна нулю и всюду внутри области. Таким образом, функции u₁ и u₂ во всей области D совпадают.

Докажем теперь непрерывную зависимость решения рассматриваемой задачи от граничного условия. Пусть u₁ и u₂ – решения двух задач Дирихле для одной и той же области, граничные условия которых различаются не более, чем на величину ε. При этом функция 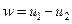гармонична, а в точках, принадлежащих границе области, отличается от нуля не более чем на ε. Если область ограничена, то в силу теоремы о максимуме и минимуме функция 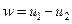не может отличаться от нуля больше, чем на ε и в любой точке внутри области. Следовательно, во всей области 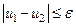, из чего и вытекает требуемое утверждение.

Теорема единственности для задачи Неймана.В этой задаче граничное условие формулируется следующим образом

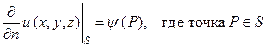(70)

Докажем сначала, что решение внутренней задачи Неймана определяется с точностью до произвольной постоянной.

Для упрощения доказательства проведем его при дополнительном предположении, что функция u имеет непрерывные первые производные во всей области, включая границу S ¹⁾.

Пусть u₁ и u₂ – две непрерывно дифференцируемые во всей области, включая границу, являющиеся решениями внутренней задачи Неймана. Тогда для разности этих функций 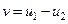будем иметь нулевое граничное условие

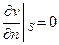(71)

Полагая в первой формуле Грина (57) 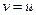и учитывая (61), получаем

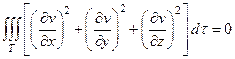
Откуда в силу дополнительногопредположения о её первых производных следует, что

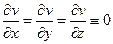, т.е. ,

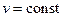Т.е. разность двух решений внутренней задачи Дирихле равна константе, что и требовалось доказать.

Изолированные особые точки

В этом параграфе мы уделим внимание особым точкам гармонических функций. При этом следует рассмотреть два случая. В первом случае гармоническая функция ограничена в окрестности особой точки, во втором – не ограничена. Ко второму случаю относится знакомая нам точка 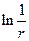– для плоскости и 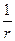– для трехмерного пространства.

Докажем теорему, согласно которой первый случай не может иметь место.

Т е о р е м а. Если гармоничная функция u(M) является ограниченной внутри области S, за исключением точки Р, то можно определить значение функции и в точке Р так, чтобы u(M) была гармонична всюду внутри области S.

Мы докажем эту теорему для плоского случая. Возьмем круг К_ε радиуса ε с центром в точке Р, целиком лежащий в внутри области S, и рассмотрим внутри этого круга гармоническую функцию v, совпадающую на его границе (окружности С_ε) с функцией и. После этого составим разность 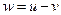, которая

1) гармонична всюду внутри К_ε , кроме точки Р, в которой w не определена,

2) непрерывно примыкает к нулевым граничным условиям на С_ε ,

3) ограничена в замкнутой области , так, что .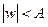

¹⁾ Доказательство единственности при более общих предположениях было дано М.В.Келдышем и М.А.Лаврентьевым (ДАН СССР, т. IV, 1937); см. также В.И.Смирнов [ ].

Построим неотрицательную гармоническую функцию следующим образом

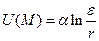
где ε – произвольное положительное число, а r – расстояние от рассматриваемой точки до точки разрыва Р.

Теперь построим круг К _δ с центром в точке Р, выбрав его радиус δ так, чтобы на его границе значение U превосходило А, и рассмотрим область К_ε – К_δ. Обратимся к функции w. Она непрерывна в замкнутой области 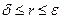и на границе этой области выполняется неравенство 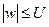. В силу принципа максимального значения неотрицательная функция U является мажорантой функции w

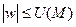для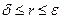

Фиксируя далее точку М области К_ε , не совпадающую с точкой Р, и осуществляя предельный переход при 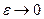, получим

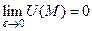
Следовательно, всюду, за исключением, может быть, точки Р, .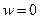

Таким образом, функция и всюду в области S, за исключением точки Р, совпадает с функцией v. Полагая теперь 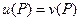, мы получим функцию и, тождественно равную функции w, гармоничную всюду внутри области S, что и доказывает теорему.

Аналогично проводится доказательство этой теоремы и для трехмерного случая с тем отличием. Что в качестве мажорантной функции будет выступать функция

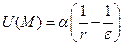
При доказательстве этой теоремы мы предполагали, что функция и ограничена в окрестности точки Р. Однако те же рассуждения остаются в силе, если предположить, что функция и в окрестности точки Р удовлетворяет неравенству

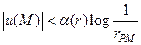, (72)

где α(r) – произвольная функция, стремящаяся к нулю при 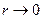. Иначе говоря, функция и в окрестности точки Р растет медленнее, чем log(1/r _PM) .

Таким образом, можно сформулировать следующее утверждение.

Если функция и (М ) является гармонической функцией внутри области S, за исключением точки Р, в окрестности которой она растет медленнее, чем log(1/r _PM) при М→Р, то эта функция является ограниченной в окрестности точки Р, и можно так определить значение u (Р ), что функция и будет гармонической во всей области S.

Аналогично, для случая трех переменных, можно доказать сформулированное утверждение следующим образом.

Если гармоническая функция и(М ) в окрестности изолированной особой точки Р растет медленнее, чем 1/r, т.е.

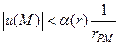при ε (r)→0, r→0,(73)

то она гармонична в окрестности этой точки, и можно так определить значение u(Р),

чтобы функция и (М ) была гармонична и в самой точке Р.