Трехмерное неоднородное волновое уравнение

Рассмотрим трехмерное неоднородное волновое уравнение

(28)

и будем искать его решение, удовлетворяющее нулевым начальным условиям

(29)

Это означает, что в исходном состоянии описываемый объект не был деформирован и покоился. В этом случае деформации этого объекта в последующие моменты времени будут определяться только внешней силой и механическими свойствами объекта.

Чтобы решить поставленную задачу нужно решить однородное уравнение

(30)

но с ненулевой начальной скоростью, равной внешней силе из уравнения (28) в некоторый момент времени τ : :

(31)

При этом τ становится параметром задачи. Иными словами воздействие внешней силы на объект заменяется на сообщение точкам объекта соответствующей скорости в некоторый

Теперь для решения задачи можно воспользоваться формулой (12) из §1, заменив в ней t на , тогда получим

? (32)

Теперь покажем, что функция , определенная формулой

,(33)

является решением неоднородного уравнения (28) при нулевых начальных условиях (29). Действительно, из формулы (33) находим

(34)

Дифференцируя теперь выражение (33) по времени, получим

,(35)

причем внеинтегральный член при равен нулю в силу первого начального условия (31), т.е.

(36)

Дифференцируя ещё раз по t, будем иметь

, (37)

причем здесь внеинтегральный член при в силу первого начального условия (31) равен , т.е.

(38)

Поскольку функция v удовлетворяет уравнению (30), то (38) можно переписать следующим образом

,

а в силу (33) входящий в это выражение интеграл есть Δu. В итоге получим

,

т.е. функция u удовлетворяет исходному уравнению (28). При этом начальные условия (29) также выполнены в силу (33) и (36).

Подставив в формулу (34) вместо функции её выражение (32), получим

Затем, если введем вместо τ новую переменную интегрирования , то получим

Вводя новые координаты

И учитывая, что , получим

,

и выражение для окончательно запишется в виде

(39)

где D_at – шар радиуса at с центром в точке (x, y, z).

Выражение (39) называют запаздывающим потенциалом, так как при выполнения интегрирования функция g берется не в рассматриваемый момент времени t, а в момент, наступивший раньше на промежуток времени r/a, необходимый для того, чтобы возмущение, распространяясь со скоростью a от точки (ξ, η, ζ ), дошло до точки (x, y, z ).

Аналогичным образом мы можем получить решение для двухмерного волнового уравнения

(40)

с нулевыми начальными данными

(41)

Это решение имеет вид

(42)

где

Точечный источник

Предположим, что свободный член в уравнении (28) отличен от нуля только в небольшой сфере D с центром в начале координат. Тогда при стремлении радиуса этой сферы ε к нулю и при синхронном возрастании интенсивности внешней силы мы в пределе можем получить решение волнового уравнения для точечного источника, который начинает действовать с момента 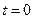по заданной зависимости от времени f (x, y, z, t).

Положим для определенности, что внутри сферы

, (43)

считая по-прежнему

при

Обратимся теперь к формуле (39) и будем считать, что , при этом, очевидно, что достаточно произвести интегрирование по шару D_ε. При ε → 0 величина r будет равна расстоянию от начала координат до точки (x, y, z), т.е. , и мы получим, учитывая (43), что

(44)

Ясно, что при , так как при область интегрирования в интеграле (39) не содержит внутри себя шара D_ε при достаточно малых ε.

Отметим, что при любом выборе функции ω(t) функция (44) удовлетворяет уравнению (28) и представляет собой сферическую волну, расходящуюся радиально со скоростью а от начала координат. При этом воздействие на точку (x, y, z) в момент времени t зависит только от отдельного импульса, возникшего в начале координат в момент времени и пришедшего в точку (x, y, z).

В случае уравнения (40) мы должны, так же как и выше, считать, что

при ,

а вместо (43) написать

,

где С_ε – круг с центром в начале координат радиуса ε.

Обращаясь к формуле (42) и переходя к пределу при ε → 0, получим решение для точечного источника на плоскости

(45)

где и