Общая схема метода разделения переменных для одномерных гиперболических уравнений

В § 5 мы познакомились с методом разделения переменных, который является одним из основных методов решения задач математической физики, в чем мы убедимся в последующих главах. Рассмотрим теперь общую схему этого метода для гиперболического уравнения более общего вида в отличие от уравнения колебаний однородной струны или однородного стержня, а именно:

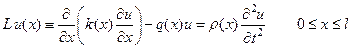, (84)

где k(x), q(x) и x(ρ) – непрерывные на отрезке 0 ≤ x ≤ l, положительные функции (k >0, ρ>0, q ≥0). Для этого уравнения сформулируем начальные условия

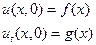t ≥ 0 (85)

и граничные условия (однородные)

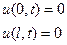(86)

В соответствии со знакомым нам методом разделения переменных будем искать нетривиальное решение уравнения (84) в виде произведения

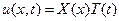(87)

Подставляя предполагаемый вид решения (87) в уравнение (84) и пользуясь граничными условиями, после операции разделения переменных получим два уравнения

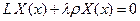(88)

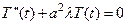(89)

где λ – неизвестный пока параметр.

В силу однородности граничных условий (86) мы можем записать однородные граничные условия и для уравнения (88):

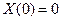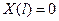и (90)

Для определения функции X (x) мы получаем известную уже задачу Штурма-Лиувилля, в которой надо найти такие значения параметра λ, при которых существует нетривиальное решение уравнения (88), удовлетворяющее граничным условиям (90), а также найти эти решения. Удовлетворяющие условиям задачи значения параметра λ называются собственными значениями или собственными числами, а соответствующие им нетривиальные решения – собственными функциями задачи Штурма-Лиувилля.

В силу однородности уравнения (88) и граничных условий (90) собственные функции определяются с точностью до постоянного множителя. Выберем этот множитель так, чтобы выполнялось равенство

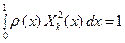, (91)

котрое представляет собой условие нормировки собственных функций.

Собственные функции, удовлетворяющие условию (91), называют нормированными. Сформулируем некоторые общие свойства собственных функций и собственных значений задачи Штурма-Лиувилля.

1. Существует счетное множество собственных значений λ₁, λ₂,…, λ_n,…, которым соответствуют собственные функции X₁(x), X₂(x),…, X_n(x),…

2. Все собственные числа при q ≥ 0 – положительны.

3. Собственные функции ортогональны между собой с весом ρ(x) на отрезке 0≤ x ≤l, т.е.

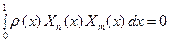(92)

4. Всякому собственному числу соответствует с точностью до постоянного множителя только одна собственная функция.

5. Произвольная дважды непрерывно дифференцируемая функция F(x), удовлетворяющая граничным условиям 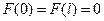, разлагается в равномерно и абсолютно сходящийся ряд по собственным функциям {X_n(x)}:

,

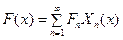причем 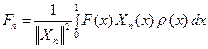, (93)

где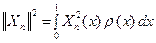

Это свойство называют теоремой разложимости Стеклова.

Доказательство свойств 1 и 5 обычно основывается на теории интегральных уравнений, которая выходит за пределы настоящего курса. Мы остановимся лишь на доказательствах свойств 2, 3 и 4.

Обратимся к доказательству свойства 3. Его удобно доказать, воспользовавшись одной из формул Грина. Мы докажем эти формулы в главе VI. Здесь нам понадобится формула Грина для дифференциального оператора, представляющего левую часть уравнения (84), а именно

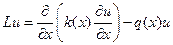
Возьмем две произвольные функции 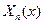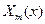, дважды непрерывно дифференцируемые на интервале 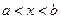и имеющие непрерывную первую производную на отрезке 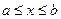. Рассмотрим теперь выражение

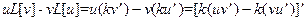(94)

Интегрируя это равенство по x от a до b, мы и получим нужную нам формулу Грина

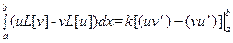(95)

Возьмем теперь две собственные функции X_n(x) и X_m(x), соответствующие собственным значениям λ_n и λ_m. Если мы положим в формуле (95) u = X_m(x), v = X_n(x), а в качестве границ интервала возьмем значения 0 и l, то учитывая граничные условия (90) получим

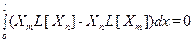, (96)

откуда, пользуясь уравнением (88), получаем

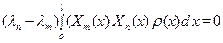(97)

Таким образом, если λ_n ≠ λ_m, то нулю равен интеграл

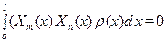(98)

что и выражает условие ортогональности собственных функций X_n(x) и X_m(x) с весом ρ(x).

Докажем теперь свойство 4.

Как мы знаем, всякая собственная функция, будучи решением обыкновенного дифференциального уравнения второго порядка, определяется однозначно по заданному значению самой функции и её первой производной в некоторой точке, например при x=0. Допустим существование двух функций X₁ и X₂, отвечающих одному и тому же значению λ и обращающихся в соответствии с граничными условиями в нуль при x=0. Тогда, если мы возьмем функцию

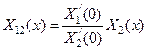, (99)

то убедимся, что она удовлетворяет тому же уравнению второго порядка (88) и тем же начальным условиям, что и функция X₁

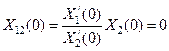, (100)

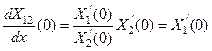. (101)

Тем самым доказано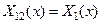, что и что

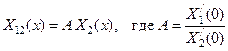
Отметим, что при определении функции X₁₂ негласно предполагалось, что 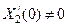. Это предположение вполне оправдано, так как решение линейного уравнения (88) для этой функции при начальных условиях

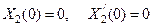
тождественно равно нулю и не может быть собственной функцией.

В силу линейности и однородности уравнения (88)

Наконец, докажем свойство 2.

Пусть X_n – нормированная собственная функция, соответствующая собственному значению λ_n , так что в соответствии с (88) мы можем написать равенство

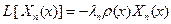(102)

Умножая обе части этого равенства на X_n и интегрируя по x от 0 до l, получаем

,

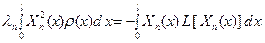тогда с учетом нормировки функции X_n получим

.

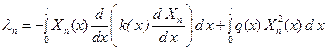Интегрируя последнее выражение по частям и пользуясь граничными условиями, получаем

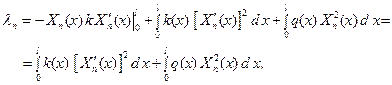
откуда и следует, что λ_n>0, поскольку по условию k (x) >0 и q(x) ≥0.

Закончив обсуждение свойств собственных функций уравнения (88), обратимся к уравнению (89). Решение этого уравнения известно и для каждого λ_n оно будет иметь вид

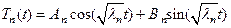(103)

где А_к и В_к – произвольные постоянные.

Тогда каждая функция

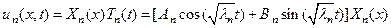
будет решением уравнения (84), удовлетворяющим граничным условиям (86). Чтобы получить общее решение уравнения (84) запишем сумму ряда

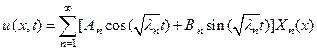
Чтобы эта сумма ряда была решением уравнения (84), нужно, чтобы сам ряд и ряды, полученные двукратным почленным дифференцированием, сходились равномерно по x и t. Для определения коэффициентов A_k и B_k воспользуемся начальными условиями (85) и теоремой разложимости Стеклова. Для этого запишем начальные условия в виде

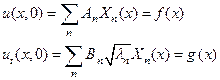
Умножим теперь обе части этих равенств на 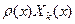и проинтегрируем по x от 0 до l. Тогда воспользовавшись условием ортогональности (92) и нормировки (91) мы получим выражения

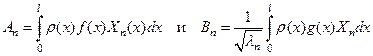(104)

Задача Гурса

В этом параграфе мы коротко познакомимся с задачей определения решения уравнения в частных производных по данным на характеристиках. Такую задачу называют задачей Гурса.

Рассмотрим задачу о колебании полубесконечной струны в случае, когда 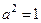. В этом случае уравнение будет иметь вид

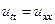(105)

К такому виду уравнения всегда можно прийти, изменив масштаб времени за счет умножения исходных единиц на коэффициент а. В результате уравнение принимает симметричный вид (63). Однако дополнительные условия вносят асимметрию в задачу, поскольку для переменной t в начальных условиях (при 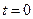) задаются две функци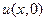и и 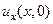, а для переменной x в граничном условии (при x=0) задается только одна функция .

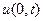Наряду с постановкой дополнительных условий на прямых x=0 и 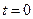на фазовой плоскости (x,t) эти условия можно ставить и на кривых в фазовой плоскости (рис. ). Например, граничные условия можно задавать на некоторой линии С₁: 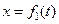, а начальные условия на некоторой линии С₂: 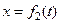. В качестве таких кривых могут выступать характеристики уравнения в частных производных.

Для некоторых уравнений координатные прямые также могут являться характеристиками. Рассмотрим, например, простейшую задачу, в которой требуется решить уравнение

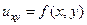(106)

с дополнительными условиями, заданными на прямых x=0 и 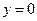, являющихся характеристиками уравнения (105):

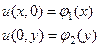(107)

Интегрируя уравнение (105) последовательно уравнение (105) по x и y, получим

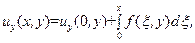
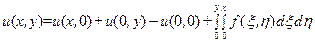
или

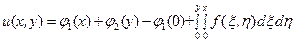(108)

Таким образом, для простейшего уравнения, не содержащего первых производных u_x, u_y и искомой функции, решение представляется в аналитической форме (108).

Рассмотрим теперь более общий вид линейного гиперболического уравнения

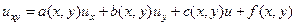
(109)

при дополнительных условиях на характеристиках x=0 и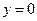

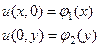(110)

где φ₁ и φ₂ удовлетворяют требованием дифференцируемости, а коэффициенты a, b и c – непрерывные функции x и y.

Последовательно интегрируя уравнение (109) по x и y, получим для функции 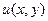интегродифференциальное уравнение

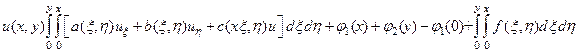(111)

Это уравнение решается приближенно с помощью метода последовательных приближений, что выходит за пределы настоящего курса.