Продольные колебания однородного стержня

Стержнем называют тело, один из размеров которого, называемый продольным, значительно превышает его размеры в плоскости, перпендикулярной к продольному направлению, т.е. поперечные размеры. Основным свойством стержня является сопротивление, оказываемое продольному сжатию (растяжению) и изгибу. Это свойство коренным образом отличает стержень от струны, которая не растягивается и не сопротивляется изгибу. Если плотность материала стержня во всех его точках одинакова, то стержень называют однородным.

Обычно в качестве стержней рассматриваются протяженные тела, ограниченные замкнутой цилиндрической поверхностью. В этом случае площадь поперечного сечения остается постоянной. Мы будем изучать поведение именно такого однородного стержня длины l, предполагая, что он подвержен только сжатию или растяжению, подчиняясь при этом закону Гука. При изучении малых продольных деформаций стержня обычно принимается так называемая гипотеза плоских сечений. Она заключается в том, что поперечные сечения, перемещаясь при сжатии или растяжении вдоль стержня, остаются плоскими и параллельными друг другу.

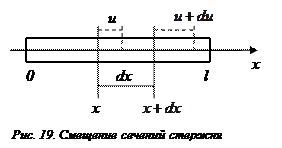Направим ось x вдоль продольной оси стержня (Рис. 19) и будем считать, что в начальный момент времени концы стержня находятся в точках x=0 и x=l. Возьмем произвольное сечение стержня с координатой x. Обозначим через u (x, t) смещение этого сечения в момент времени t, тогда смещение сечения с координатой 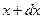в тот же момент времени будет равно

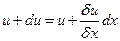
Тогда относительное удлинение стержня в сечении x будет равно

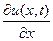
Сила сопротивления этому удлинению по закону Гука будет равна

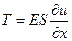, (66)

где E – модуль упругости материала стержня (модуль Юнга), а S – площадь поперечного сечения. На границах участка стержня длиной dx на него действуют силы T_x и T_x+dx , направленные вдоль оси x. Результирующая эти их сил будет равна

,

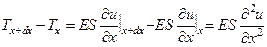а ускорение рассматриваемого участка стержня равно 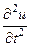, тогда уравнение движения этого участка стержня будет иметь вид:

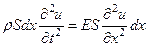, (67)

где ρ – плотность материала стержня. Если эта плотность и модуль Юнга, постоянны , то можно ввести величину 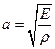через и, поделив обе части уравнения на Sdx, окончательно получить уравнение продольных колебаний стержня в отсутствии внешних сил

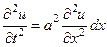(68)

Это уравнение по форме совпадает с уравнением поперечных колебаний струны и методы решения для него те же, однако, коэффициентом a в этих уравнениях обозначены разные величины. В уравнении струны величина a² представляет дробь,в числителе которой стоит постоянная сила натяжения струны – Т, а в знаменателе линейная плотность ρ, а в уравнении струныв числители стоит модуль Юнга, а в знаменателе – объемная плотность материала стержня ρ. Отсюда и физический смысл величины a в этих уравнениях разный. Если для струны этот коэффициент является скоростью распространения малого поперечного смещения, то для стержня он является скоростью распространения малого продольного растяжения или сжатия и называется скоростью распространением звука, поскольку именно с этой скоростью будут распространяться по стержню малые продольные колебания, представляющие собой звук.

Для уравнения (68) задаются начальные условия, которые определяют смещение и скорость смещения любого сечения стержня в начальный момент времени:

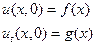(69)

Для ограниченного стержня задаются условия закрепления или приложения силы на его концах в виде граничных условий 1-го, 2-го и 3-го рода.

Граничные условия первого рода задают продольное перемещение на концах стержня:

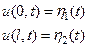(70)

Если концы стержня закреплены неподвижно, то в условиях (6) 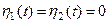. В этом случае, так же как и в задаче о колебании защемленной струны применим метод разделения переменных.

В граничных условиях II рода на концах стержня задаются упругие силы, образующиеся в результате деформации по закону Гука в зависимости от времени. Согласно формуле (66) эти силы с точностью до постоянного множителя равны производной u_x, поэтому на концах и задаются эти производные как функции времени:

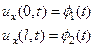(71)

Если один из концов стержня свободен, то на этом конце u_x = 0.

Граничные условия третьего рода могут быть представлены как условия, при которых к каждому концу стержня прикреплена пружина, другой конец которой перемещается вдоль оси по заданному закону времени θ (t), как это изображено на Рис. 20. Эти условия могут быть записаны следующим образом

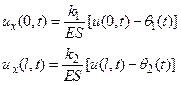, (72)

где k₁ и k₂ – жесткости пружин.

Если на стержень вдоль оси действует ещё и внешняя сила p (x, t), рассчитанная на единицу объема, то вместо уравнения (50) следует записать неоднородное уравнение

,

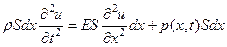Которое, после деления на 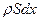примет вид

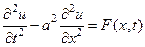, (73)

где 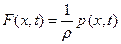. Уравнение (73) представляет собой уравнение вынужденных продольных колебаний стержня, которое решается по аналогии с уравнением вынужденных колебаний струны.

Замечание.Следует заметить, что и струна и стержень являются моделями реальных тел, которые в действительности могут проявлять как свойства струны, так и стержня, в зависимости от условий, в которых они находятся. Кроме того, в полученных уравнениях не учитываются силы сопротивления окружающей среды и силы внутреннего трения, в результате чего эти уравнения описывают незатухающие колебания. Для учета эффекта затухания в простейшем случае используется диссипативная сила, пропорциональная скорости и направленная в сторону, противоположную движению, т.е. скорости. В результате уравнение (73) принимает вид

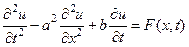(74)