Прогнозирование объема испытаний

Анализ поведения случайных траекторий 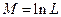показывает, что моменты окончания испытаний являются случайными величинами ( см. рис. 6.3).

Причем в случае приемки партии выполняется соотношение

,

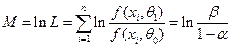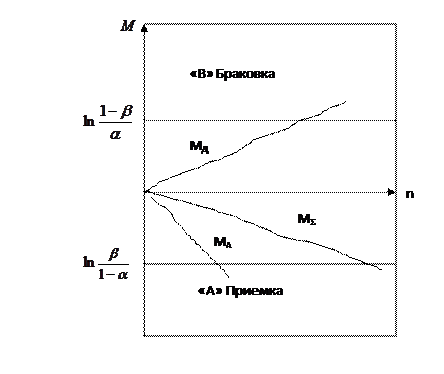
Рис. 6.3 Траектории случайных реализаций значений M(n)=Ln{L(n)}

В этом случае вероятность приемки правильной гипотезы равна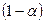

Соответственно, если произойдет браковка, то

,

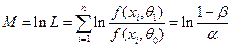При этом вероятность браковки правильной гипотезы равна .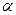

Можно доказать, что

.

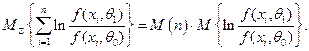С другой стороны математическое ожидание можно оценить по соотношению ( см. рис.6.3)

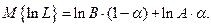
Отсюда

,

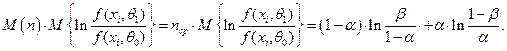где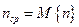

Таким образом

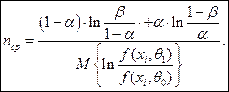
Для нормального закона распределения средний объем испытаний, необходимый для подтверждения заданного показателя надежности, определяется по формуле ( )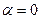

.

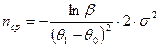Пример выполнения задания №.2.1

Результаты расчетов представлены ниже:

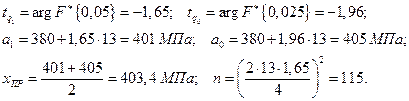
Заметим, что для партии листов с принятыми характеристиками, вероятность брака будет равна

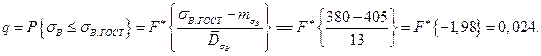
Занятие №8

Расчет числа отказов и обьема ЗИПа.

Задание

Оценить количество отказов для стратегии аварийных замен

1.1 Привести график функции восстановления для случаев

а) общего резервирования.

б) «холодного» резервирования,

в) «горячего» резервирования,

1.2 Рассчитать среднее число отказов и оценить гарантированный объем ЗИПа при следующих исходных данных: , .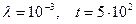

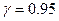Привести ассинптотическую оценку объема ЗИПа.

Основные расчетные соотношения

Стратегия аварийных замен.

Стратегия связана с простейшей моделью ремонта: после каждого отказа система приводится в исправное состояние за пренебрежимо короткое время и тотчас же возвращается в рабочее состояние. При этом под ремонтом понимается полное восстановление всех исходных свойств системы. Эта модель представляет собой хорошее приближение прежде всего для той практической ситуации, когда имеются резервные системы одного типа. В этом случае теория дает хорошие результаты для планирования потребностей в запасных частях. Исследование рассмотренных вопросов основывается на математической теории восстановления. В дальнейшем, при проведении анализа будем считать, что элемент начинает свою работу в момент t=0 и, проработав случайное время τ₁, выходит из строя. В этот момент он заменяется новым элементом, который, проработав время τ₂, выходит из строя и заменяется третьим элементом. Этот процесс продолжается неограниченно. Естественно предположить, что времена жизни элементов τ₁, τ₂, ... независимы. Случайные времена τ₁, τ₂, ... имеют один и тот же закон распределения, который мы обозначим через F(t):

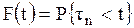
Моменты отказов (рис.7.1) или восстановлений t₁ = τ₁ , t₂ = τ₁ + τ₂ , … , t_n = τ₁ + … + τ_n, образуют случайный поток, который мы будем называть процессом восстановления.

Рис.7.1 Схема процесса восстановления

Фундаментальное значение при изучении процесса восстановления играет так называемая функция восстановлении H(t), которая равна среднему числу отказов, происшедших до момента t.

Можно показать, что функция H(t) удовлетворяет интегральному уравнению

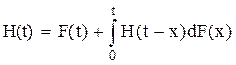
Вместо функции H(t) часто рассматривают дифференциальную характеристику

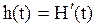
Функция h(t) называется плотностью восстановления.

Плотность восстановления удовлетворяет уравнению восстановления:

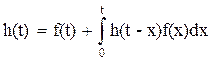
Применяя преобразование Лапласа к уравнению восстановления , получим:

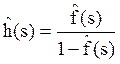
Под преобразованием Лапласа функции f(t) принимают функцию

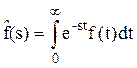
Таблица преобразований Лапласа представлена ниже

Преобразования Лапласа Таблица 7.1

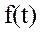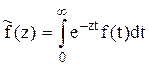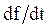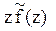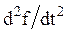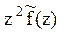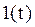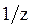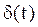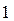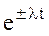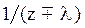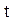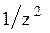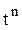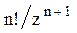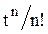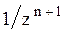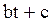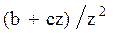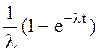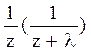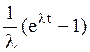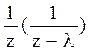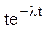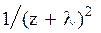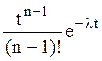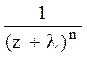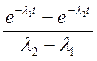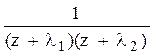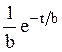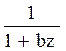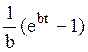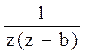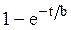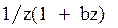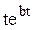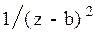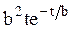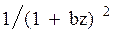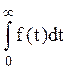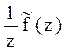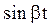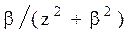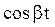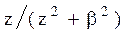Полученные результаты позволяют оценивать необходимое количество запасных частей.

Для экспоненциального закона распределения функция и плотность восстановления оцениваются по соотношениям

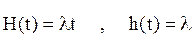
Очевидно среднее количество запасных частей не обеспечивает гарантированного результата, так как реально число отказов 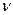может больше, чем их среднее число . Гарантированное число резервных элементов можно оценить из условия

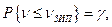
где 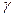- заданный уровень доверия; 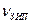- число запасных элементов.

Для экспоненциального закона распределения наработки на отказ соотношение примет вид

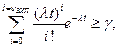
где 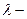интенсивность отказа; 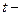заданное время работы устройства.

При длительном функционировании можно найти ассинптотическую оценку числа отказов. В этом случае случайное число отказов имеет нормальное распределение с параметрами

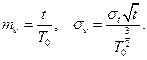
Очевидно гарантированное количество запасных частей может быть найдено из условия

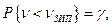
где 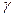- принятый уровень доверия.

Раскрывая выражение для вероятности, получим

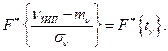
Отсюда

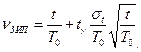
Пример выполнения задания №1.1а

Граф переходов имеет вид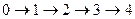

переход 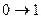происходит с интенсивностью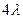

переход 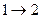происходит с интенсивностью 3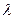

По графу составляем уравнения Колмогорова

, ,

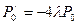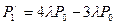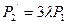
Беря преобразование Лапласа от обеих частей уравнения, получим

, ,

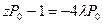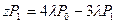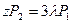
После преобразований получим

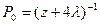
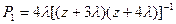
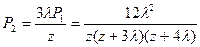
Согласно свойству преобразования Лапласа имеем

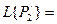
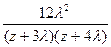= f(z)

Отсюда

1-f(z)=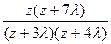

Таким образом преобразование Лапласа плотности восстановления будет равно

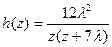
Производя обратное преобразование получим

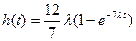
Функция восстановления находится интегрированием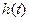

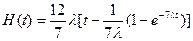
2. Рассчитать средний срок службы трубопровода для следующих исходных данных:

2.1 , , , ,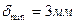

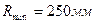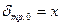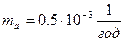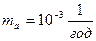
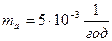
2.2 Оценить 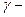процентный ресурс трубопровода ( ).

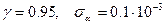Основные расчетные соотношения

Использование стратегии аварийных замен неприемлемо для тех ситуаций, когда отказ системы приводит к катастрофическим последствиям. В этих случаях назначают гарантированный ресурс. Согласно ГОСТ 27.002-83 вводится понятие гамма-процентного ресурса, который характеризует наработку, в течении которой объект не достигнет предельного состояния с заданной вероятностью 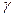, выраженной в процентах. Величину гамма-процентного ресурса можно определить по соотношению

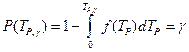
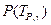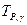где - вероятность обеспечения ресурса , соответствующего заданному уровню доверительной вероятности ,

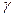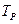- наработка до предельного состояния.

Основой случайных процессов изменения параметров работоспособности являются необратимые случайные изменения, вызванные старением, из­носом или разрегулированием и имеющие определенную зави­симость от времени. В частности при оценке надежности трубопровода считается, что определяющий параметр изменяется по экспоненциальному закону

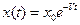, где 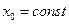, а V – подчиняется нормальному закону.

Логарифмируя, получим .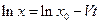

Вводя обозначения: 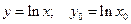, приходим к линейной зависимости

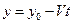
Следовательно для рассматриваемого случая можно воспользоваться результатами, полученными для веерной функции. Для иллюстрации рассмотрим пример оценки надежности трубопровода с учетом коррозии. В общем случае закон снижения толщины трубы при воздействии коррозии можно оценить по соотношению 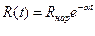, где 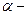случайная скорость изменения радиуса трубы в течении ее эксплуатации.

Изменение работоспособной толщины трубы в процессе эксплуатации представлено на рис.7.2

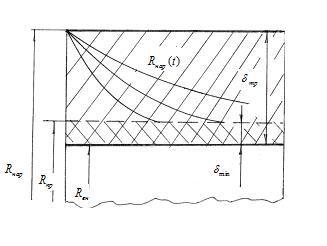
Рис. 7.2 Расчетная схема функционирования трубопровода.

с учетом старения.

На рисунке введены следующие обозначения: 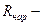начальный наружный радиус трубы;

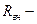внутренний радиус трубы; 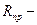предельное значение внешнего радиуса;

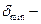минимальная толщина трубы, обеспечивающая ее работоспособность.

В рассматриваемом случае среднее время до отказа трубопровода будет равно

,

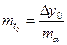где 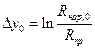- запас работоспособности трубы [ 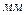] ; 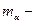математическое ожидание скорости коррозии [ ] .

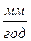Если имеется непрерывная случайная величина х с плотностью распределения f(x), а другая случайная величина t связана с нею функцио­нальной зависимостью t=φ(x), то плотность распреде­ления случайной величины t определяется соотношением

g(t) = f(ψ(t)) | ψ^/(t) |

где ψ — функция, обратная функции φ.

Рассмотрим это правило применительно к первому варианту.

Пусть определяющий параметр изменяется (напри­мер, увеличивается) линейно во времени

x(t) = x₀+Vt

где x₀ и V — начальное значение и скорость, изменения во времени определяющего параметра.

При этом начальное значение параметра практически постоянно (х₀==соnst), а скорость изменения определяющего параметра во времени, будучи постоянной в каждой конкретной реализации, от реализации к реализации меняется случайным образом, в частности по нормальному закону:

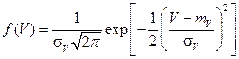
где т_V, σ_V — МОЖ и среднеквадратическое отклонение скорости изменения во времени параметра x. Рассматриваемый случай представлен на рис.7.3 .

x

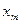
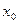
0 t

Рис.7.3. График веерной функции x(t)

При этом случайная величина наработки t до отказа связана с начальным и предельным значениями, а также со случайной скоростью V изменения во времени параметра х следующей функциональной зависимостью:

t = Δx/V,

где Δx = (x_m-x₀) — детерминированная величина, харак­теризующая запас работоспособности (долговечности) по параметру х.

Отсюда

Ψ(t) = Δx/t

В свою очередь, из этого выражения следует

| Ψ΄(t)| = Δx/t²

После подстановки получим:

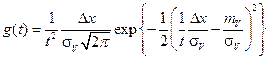
Обозначим:

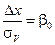
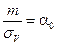
С учетом введенных обозначений получаем

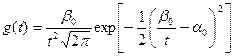
Пример выполнения задания №2.1

Результаты расчета среднего срока службы трубопровода в зависимости от исходной толщины трубы для различных скоростей коррозии представлены на рис.7.4 При проведении расчета были приняты следующие исходные данные:

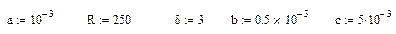
Расчеты проводились по соотношениям

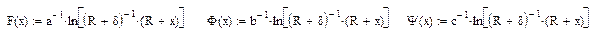
Результаты расчета представлены на рис. 7.4

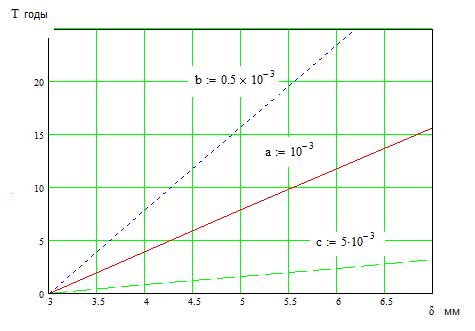
Рис.7.4 Зависимость срока службы трубопровода 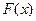в годах от толщины

трубы x= 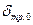в мм для различных значений скорости коррозии.

Занятие №9