Расчитать нижнюю границу доверительного интервала надежности системы
2.1
| Число испытаний | ||||
| Число отказов |
2.2
| Число испытаний | ||||
| Число отказов |
Основные расчетные соотношения
При проведении испытаний по схеме «успех-отказ» нижняя граница надежности является корнем уравнения
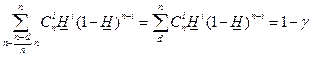
В частности, для безотказных испытаний, полагая d=n , из соотношения получим 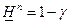 . Отсюда
. Отсюда 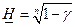
Рассмотренный метод позволяет производить оценки надежности 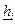 отдельных элементов, входящих в состав системы. Однако при решении практических задач возникает потребность оценки надежности системы в целом
отдельных элементов, входящих в состав системы. Однако при решении практических задач возникает потребность оценки надежности системы в целом 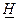 при известных результатах испытаний ее отдельных элементов. В дальнейшем будем искать решение этой задачи для систем с последовательным соединением элементов. Строгое решение этой задачи получено при проведении испытаний по схеме «успех-отказ»
при известных результатах испытаний ее отдельных элементов. В дальнейшем будем искать решение этой задачи для систем с последовательным соединением элементов. Строгое решение этой задачи получено при проведении испытаний по схеме «успех-отказ»
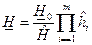 ,
,
где 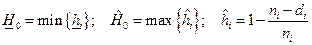 .
.
Следует заметить, что это соотношение является обобщением частного случая, соответствующего безотказным испытаниям
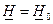
При других схемах проведения испытаний для нахождения интервальной оценки надежности системы используется приближенное соотношение
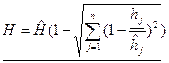
Пример выполнения задания №2.1
Точечная оценка надежности : 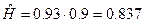
Нижняя граница доверительного интервала :
Схема «успех-отказ»: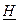 =
= 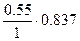 =0.46
=0.46
Общий случай :
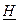 =
= 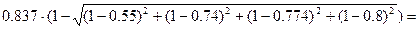 0.335
0.335
Оценить потребный объем испытаний k-го элемента системы при проведении автономных испытаний, оптимальный уровень надежности k-го элемента и коэффициент запаса, закладываемый на этапе его проектной разработки. Закон распределения параметра работоспособности элемента считать нормальным.
3.1 При проведении расчетов принять следующие исходные данные:
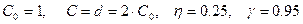
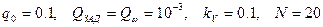
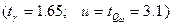
3.2 При проведении расчетов принять следующие исходные данные:
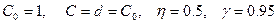
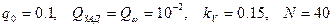
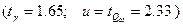
Основные расчетные соотношения
При решении задачи планирования автономных испытаний будем предполагать, что изделие может быть представлена в виде системы с последовательно соединенными элементами. В этом случае надежность системы H равна
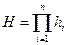 , где hi – надежность i-го элемента.
, где hi – надежность i-го элемента.
Для высоконадежных систем имеем
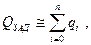 где qi =1- hi.- вероятность отказа i- го элемента.
где qi =1- hi.- вероятность отказа i- го элемента.
Соответственно точечная оценка вероятности отказа будет равна
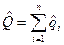 , где
, где 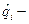 точечная оценка вероятности отказа i-го элемента.
точечная оценка вероятности отказа i-го элемента.
Для расчета верхней границы вероятности отказа системы 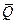 можно воспользоваться интервальной оценкой
можно воспользоваться интервальной оценкой
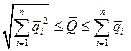 ,
,
где 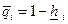 ;
; 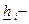 нижняя граница надежности i-го элемента системы.
нижняя граница надежности i-го элемента системы.
Нижняя граница надежности элемента 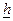 , прогнозируемая после проведении k испытаний , в случае нормального распределения параметров работоспособности, может быть оценена по соотношению
, прогнозируемая после проведении k испытаний , в случае нормального распределения параметров работоспособности, может быть оценена по соотношению
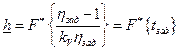 ,
,
где 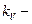 коэффициент вариации коэффициента параметрического запаса
коэффициент вариации коэффициента параметрического запаса  ;
;
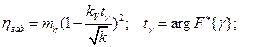
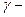 уровень доверительной вероятности;
уровень доверительной вероятности;
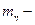 математическое ожидание коэффициента запаса; k- число испытаний;
математическое ожидание коэффициента запаса; k- число испытаний;
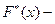 функция нормированного нормального распределения .
функция нормированного нормального распределения .
Таким образом потребный уровень математического ожидания коэффициента запаса удовлетворяет соотношению
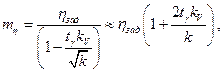
После преобразований будем иметь
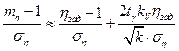 ,
,
Введя обозначения 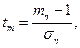
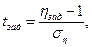
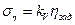 ,
,
получим 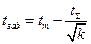 .
.
Таким образом 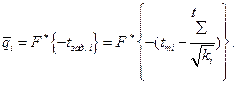 , где
, где 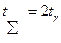 .
.
Следовательно, требуемый уровень надежности может быть подтвержден при различных комбинациях параметров tmi и 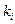 . Среди многообразия этих значений целесообразно выбрать те, которые обеспечивают заданный уровень вероятности отказа при минимальных затратах средств.
. Среди многообразия этих значений целесообразно выбрать те, которые обеспечивают заданный уровень вероятности отказа при минимальных затратах средств.
Очевидно, уровень избыточности элементов системы tmi будет определять производственные и эксплуатационные расходы на выполнение программы:
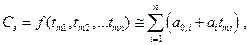
где 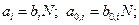 N – объем выпускаемой продукции;
N – объем выпускаемой продукции;
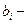 коэффициент чувствительности, характеризующий удельные затраты
коэффициент чувствительности, характеризующий удельные затраты
на обеспечение единицы надежности, выраженной в гауссах.
Параметр 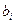 определяется уровнем избыточности элемента. В частности, при использовании «горячего» резерва вероятность отказа резервной группы
определяется уровнем избыточности элемента. В частности, при использовании «горячего» резерва вероятность отказа резервной группы 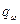 оценивается по соотношению
оценивается по соотношению
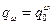 ,
,
где 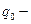 вероятность отказа нерезервированного элемента;
вероятность отказа нерезервированного элемента; 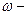 условная кратность резерва.
условная кратность резерва.
Отсюда 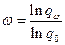 .
.
Очевидно стоимость резервированного элемента будет равна
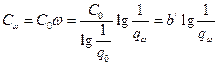 ,
,
где 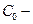 стоимость нерезервированного элемента;
стоимость нерезервированного элемента;
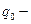 вероятность отказа нерезервированного элемента;
вероятность отказа нерезервированного элемента;
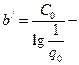 затраты на единицу надежности, выраженной в беллах.
затраты на единицу надежности, выраженной в беллах.
Переходя к оценке надежности в гауссах, получим
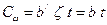 , где
, где 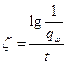 ;
; 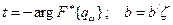 .
.
В общем случае зависимость стоимости от кратности резерва можно представить в виде
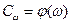
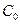 .
.
Вид функции 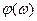 зависит от типа резервирования .Как было показано выше, в случае «горячего» резерва , имеем
зависит от типа резервирования .Как было показано выше, в случае «горячего» резерва , имеем 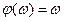 .
.
В дальнейшем найдем аналогичные соотношения для элементов с параметрической избыточностью. При решении поставленной задачи, вероятность отказа элементов с параметрической избыточностью условно представим в виде
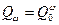
где 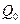 - вероятность отказа элемента, соответствующая коэффициенту запаса
- вероятность отказа элемента, соответствующая коэффициенту запаса 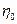 ;
; 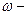 условная кратность резерва.
условная кратность резерва.
Надежность элемента 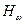 ,прогнозируемая после проведении k испытаний , может быть оценена по соотношению
,прогнозируемая после проведении k испытаний , может быть оценена по соотношению
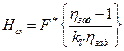 ,
,
где 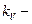 коэффициент вариации коэффициента запаса;
коэффициент вариации коэффициента запаса;
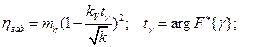
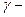 уровень доверительной вероятности;
уровень доверительной вероятности;
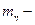 математическое ожидание коэффициента запаса.
математическое ожидание коэффициента запаса.
Знание 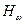 , позволяет оценить условную кратность резерва
, позволяет оценить условную кратность резерва 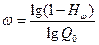 ,
,
В дальнейшем будем считать, что стоимость резервированного элемента пропорциональна коэффициенту запаса 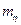 . Тогда функцию
. Тогда функцию 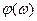 можно оценить по соотношению
можно оценить по соотношению 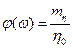 . Характер изменения функции
. Характер изменения функции 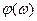 представлен на рис. 5.1
представлен на рис. 5.1
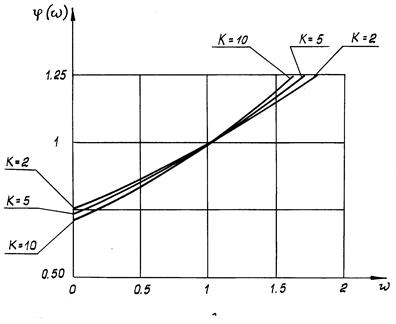
Рис.5.1 Характер изменения функции 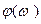 для элементов с параметрической избыточностью.
для элементов с параметрической избыточностью.
При построении графика было приняты следующие исходные данные:
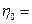 1.3 ;
1.3 ; 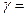 0,95 ;
0,95 ; 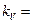 0,1 ;
0,1 ; 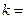 2, 5, 10.
2, 5, 10.
Как видно из графика функция 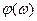 слабо зависит от объема испытаний k . Приближенно для функции
слабо зависит от объема испытаний k . Приближенно для функции 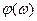 может быть принята линейная аппроксимационная зависимость
может быть принята линейная аппроксимационная зависимость
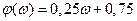 .
.
С учетом полученных результатов, выражение для стоимости примет вид
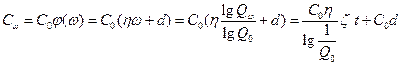 ,
,
где 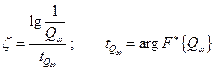
Отсюда
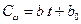 , где
, где 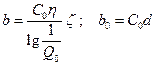 .
.
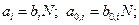 N – объем выпускаемой продукции;
N – объем выпускаемой продукции;
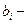 коэффициент чувствительности, характеризующий удельные затраты
коэффициент чувствительности, характеризующий удельные затраты
на обеспечение единицы надежности, выраженной в гауссах.
Соответственно затраты на экспериментальную отработку будут определяться объёмами испытаний элементов
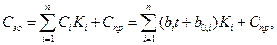
где Ci - затраты на проведение одного испытания i-го элемента,
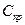 – затраты, не зависящие от варьирующихся параметров.
– затраты, не зависящие от варьирующихся параметров.
Таким образом, решение задачи сводится к минимизации функции суммарных затрат
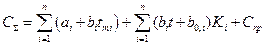
В качестве дисциплинирующего условия рассмотрим правую границу неравенства
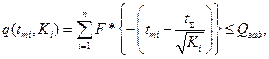
В дальнейшем для нахождения оптимального решения задачи рассмотрим функцию Лагранжа
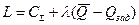
Оптимальные параметры будут удовлетворять системе алгебраических уравнений:
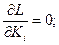
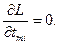
При нахождении производной 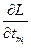 , предполагая, что число испытаний
, предполагая, что число испытаний 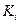 существенно меньше объема транспортной программы N, вторым слагаемым в выражении (2.36) можно пренебречь. Поэтому в дальнейшем удельные затраты на проведение одного испытания
существенно меньше объема транспортной программы N, вторым слагаемым в выражении (2.36) можно пренебречь. Поэтому в дальнейшем удельные затраты на проведение одного испытания 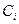 будем считать постоянными для каждого i-го элемента системы.
будем считать постоянными для каждого i-го элемента системы.
Производя дифференцирование, получим:
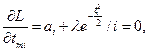
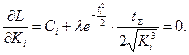
Разрешая систему уравнений относительно Ki, найдем
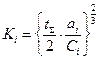
Соотношение позволяет оценить оптимальный объем испытаний с точностью до целых. Таким образом оптимальные объемы испытаний отдельных элементов не зависят от требований, предъявляемых к надежности систем и определяются соотношением удельных затрат на обеспечение единицы надежности, закладываемой на этапе проектирования, 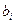 и затрат на проведение одного испытания
и затрат на проведение одного испытания 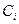 .
.
Соответственно, из первого уравнения системы получим:
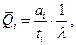
где 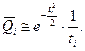
Подставляя 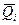 в граничное условие , приходим к соотношению:
в граничное условие , приходим к соотношению: 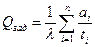 . Отсюда
. Отсюда 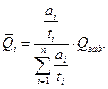
Таким образом, оптимальные уровни вероятности отказа пропорциональны удельным затратам 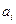 и заданным требованиям к вероятности отказа системы
и заданным требованиям к вероятности отказа системы 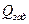 .
.
Потребные уровни коэффициента запаса, закладываемые на этапе разработки изделия, оцениваются по соотношениям
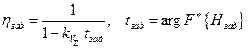 .
.
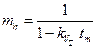 , где
, где 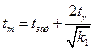 .
.
Пример выполнения задания № 3.1
Оптимальный объем испытаний оценивался по соотношению
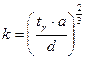 , где
, где 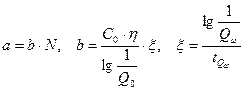
Программа вычислений и результаты расчета представлены ниже (см. рис.5.2)
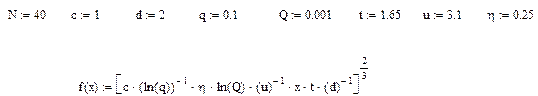
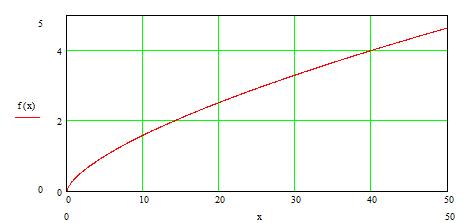
Рис. 5.2 Зависимость числа испытаний i-ой системы на этапе автономной отработки
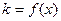 от объема транспортной программы (x=N).
от объема транспортной программы (x=N).
При разработке программы были приняты обозначения;
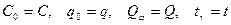 .
.
Занятие №6
