Образцы выполнения лабораторных работ
Приднестровский государственный университет
им. Т.Г. Шевченко
Физико-математический факультет
Кафедра «Алгебры, геометрии и методики преподавания математики»
Лабораторная работа №1
Вариант №___
Тема: «Функциональная зависимость. Нахождение области определения функции. Правила преобразования графиков функций»
Выполнил(а) студент(ка)
медицинского факультета,
гр. ______
специальность «_________________»
Ф.И.О.
Проверил преподаватель
Ф.И.О.
| Дата сдачи | Дата возврата | Дата сдачи | Дата возврата | |
Тирасполь, 2017 г.
Тема: «Функциональная зависимость. Нахождение области определения функции. Правила преобразования графиков функций»
Знания:
- определение функции;
- определение чётности, нечётности;
- определение периодической функции;
- определение возрастающей, убывающей функции.
Умения:
- производить элементарные операции с функциями;
- находить область значений, область определений функций;
- строить графики функций по шагам.
Задание 1.
Дана функция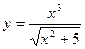 . Вычислить значение выражения
. Вычислить значение выражения 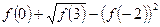 .
.
Решение.
Составим таблицу, принимая 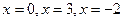 . Она имеет вид:
. Она имеет вид:
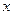 | -2 | ||
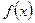 | 7,216 | -2,667 |
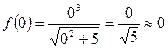 ;
; 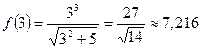 ;
; 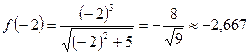 .
.
Т. об., 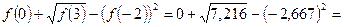
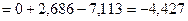 .
.
Ответ: значение выражения 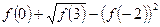 примерно равно
примерно равно 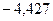 .
.
Задание 2.
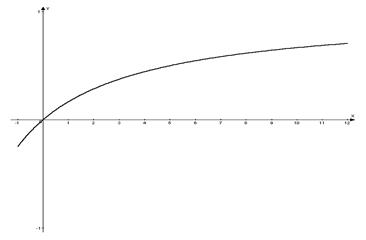
Составить таблицу значений функции 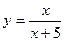 на промежутке
на промежутке 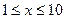 с шагом
с шагом 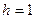 и построить ее график.
и построить ее график.
Решение.
Составим таблицу:
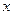 | ||||||||||
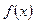 | 0,2 | 0,3 | 0,4 | 0,44 | 0,5 | 0,55 | 0,6 | 0,62 | 0,64 | 0,7 |
Найдем соответствующие значения функции.
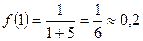
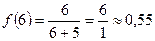
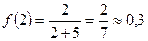
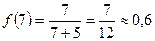
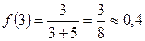
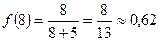
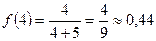
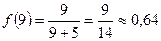
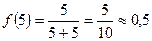
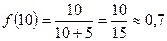 .
.
Задание 3.
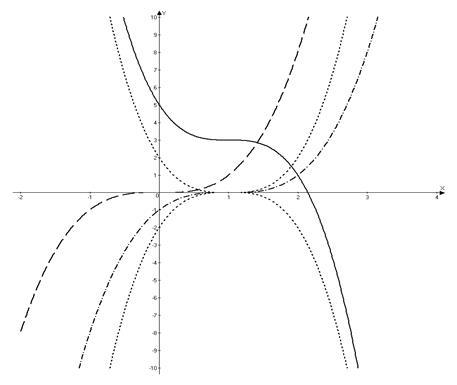
Построить по шагам график функции, используя правила преобразования графиков.
а) 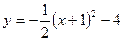
Необходимо начать построение с графика элементарной функции. В данном случае – это парабола 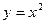 . А затем, преобразовывая предыдущий график построить заданную функцию
. А затем, преобразовывая предыдущий график построить заданную функцию 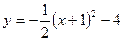 .
.
1) 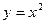 ; 2)
; 2) 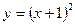 ; 3)
; 3) 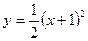 ; 4)
; 4) 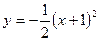 ; 5)
; 5) 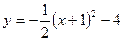 .
.
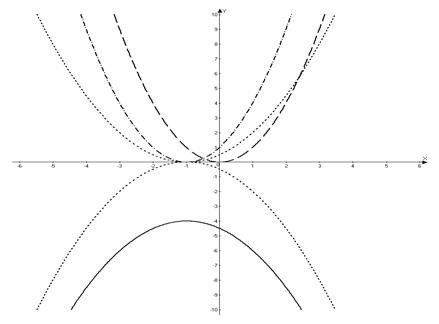
б) 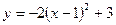
Необходимо начать построение с графика элементарной функции. В данном случае – это кубическая парабола 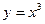 . А затем, преобразовывая предыдущий график построить заданную функцию
. А затем, преобразовывая предыдущий график построить заданную функцию 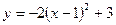 .
.
1) 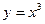 ; 2)
; 2) 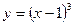 ; 3)
; 3) 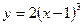 ; 4)
; 4) 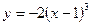 ; 5)
; 5) 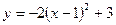 .
.
Задание 4.
Найти область определения функции 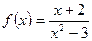 .
.
Решение.
В числителе ничего особенного нет, а вот знаменатель должен быть ненулевым. Давайте приравняем его к нулю и попытаемся найти точки, обращающие в нуль знаменатель:
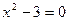
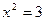
Полученное уравнение имеет два корня: 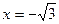 и
и 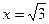 . Данные значения не входят в область определения функции. Действительно, подставьте
. Данные значения не входят в область определения функции. Действительно, подставьте 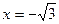 или
или 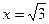 в функцию
в функцию 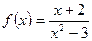 и вы увидите, что знаменатель обращается в ноль.
и вы увидите, что знаменатель обращается в ноль.
Рисуем числовую ось и расставляем точки в порядке возрастания
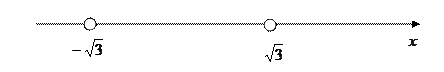

Т. об., область определения функции имеет вид:
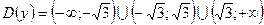
Ответ: область определения: 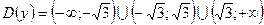 .
.
Задание 5.
Выяснить, является функция четной, нечетной или общего вида
1) 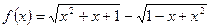
Подставим вместо 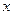 значение
значение 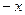 , получим
, получим
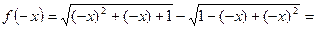
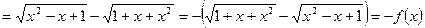
Т. к. выполняется условие 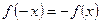 , следовательно, функция нечетная.
, следовательно, функция нечетная.
2) 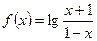
Подставим вместо 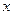 значение (
значение ( 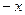 ), получим
), получим
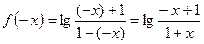 .
.
Исходную функцию не получили, а получили совсем другую – значит, исходная функция не является ни четной, ни нечетной.
Приднестровский государственный университет
им. Т.Г. Шевченко
Физико-математический факультет
Кафедра «Алгебры, геометрии и методики преподавания математики»
Лабораторная работа №2
Вариант №___
Тема: «Производная функции, ее применение к приближенным вычислениям и исследованию функций»
Выполнил(а) студент(ка)
медицинского факультета,
гр. ______
специальность «_________________»
Ф.И.О.
Проверил преподаватель
Ф.И.О.
| Дата сдачи | Дата возврата | Дата сдачи | Дата возврата | |
Тирасполь, 2017 г.
