Элементы дисперсионного анализа
Дисперсионный анализ – статистический метод, предназначенный для оценки влияния различных факторов на результат эксперимента, а также для последующего планирования аналогичных экспериментов.
Мы будем рассматривать однофакторный дисперсионный анализ.
На практике дисперсионный анализ применяют, чтобы установить, оказывает ли на изучаемую величину Х существенное влияние некоторый качественный фактор F, который имеет m уровней F1, F1, …, Fm. Число испытаний одинаково и равно n.
Основная идея дисперсионного анализа состоит в сравнении «факторной дисперсии», порождаемой воздействием фактора, и «остаточной дисперсии», обусловленной случайными причинами. Если различие между этими дисперсиями значимо, то фактор оказывает существенное влияние на Х; в этом случае средние наблюдаемых значений на каждом уровне (групповые средние) различаются значимо. Другими словами, проверяется нулевая гипотеза Н0 о равенстве математических ожиданий.
Для этого находятся:
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Средний квадрат |
| Межгрупповая (факторная)сумма квадратов отклонений Внутригрупповая (остаточная) сумма квадратов отклонений Общая (полная) сумма квадратов отклонений | 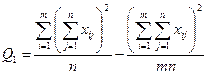 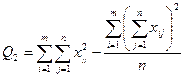 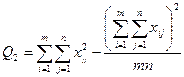 | k1=m–1 k2=m(n –1) k=mn–1 |   |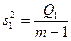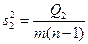
В случае однофакторного комплекса условий средние квадраты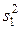 
и 
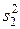являются несмещенными выборочными оценками одной и той же дисперсии s2.
Таким образом, проверка нулевой гипотезы Н0 сводится к проверке существенности различия 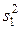и .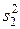
Гипотеза Н0 отвергается, если фактически вычисленное значение статистики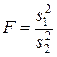 
больше критического Fa, k1, k2, определенного на уровне значимости a по таблице критических точек распределения F Фишера-Снедекора (приложение 8), и принимается, если F£ Fa, k1, k2.
Пример 7.2.1. Произведено 3 испытания на каждом из четырех уровней. Результаты испытаний приведены в таблице:
| Номер испытания | Уровни фактора Fj | |||
| i Fj | F1 | F2 | F3 | F4 |
Методом дисперсионного анализа при уровне значимости 0,01 проверить нулевую гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.
○ В нашем случае имеем m=3, n=4. Заполним таблицу, для этого найдем:
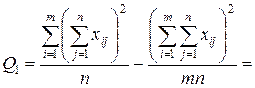
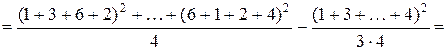
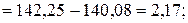
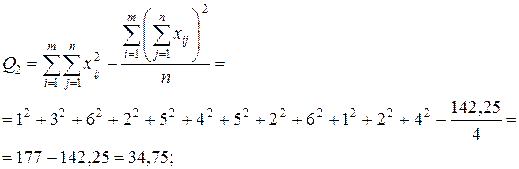
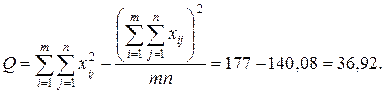
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Средний квадрат |
| Межгрупповая (факторная)сумма квадратов отклонений Внутригрупповая (остаточная) сумма квадратов отклонений Общая (полная) сумма квадратов отклонений | 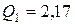 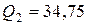 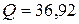 | k1=2 k2=9 k=11 |   |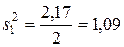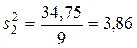
Тогда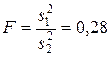 
.
По таблице критических точек распределения F Фишера-Снедекора (Приложение 8) F0,01, 2, 9=8,02.
Поскольку F0,01, 2, 9>F, то H0 принимаем. Следовательно, влияние фактора незначительно.●
[1] В таком случае говорят, что сходится к Θ по вероятности.