Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки)
Пусть генеральные совокупности Х и Y распределены нормально, причем их дисперсии неизвестны. Так, по выборкам малого объема нельзя получить хорошие оценки генеральных дисперсий. По этой причине нельзя применить метод сравнения средних, изложенный в 6.2.3.
Однако, если дополнительно предполагать, что неизвестные генеральные дисперсии равны между собой, то существует критерий (Стьюдента) сравнения средних. Например, если сравниваются средние значения диаметров таблеток, изготовленных на одном и том же станке, то естественно допустить, что дисперсии контролируемых размеров одинаковы.
Если же нет оснований считать дисперсии одинаковыми, то, прежде чем сравнивать средние, следует, пользуясь критерием Фишера–Снедекора (см. 6.2.2.), предварительно проверить гипотезу о равенстве генеральных дисперсий.
Итак, в предположении, что генеральные дисперсии одинаковы, требуется проверить нулевую гипотезу Н0: М(X)=М(Y) о равенстве математических ожиданий, другими словами, требуется установить, значимо или незначимо различаются выборочные средние 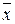 и
и 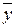 , найденные по независимым малым выборкам объемов n1 и n2.
, найденные по независимым малым выборкам объемов n1 и n2.
Случай 1. Для того, чтобы при заданном уровне значимости a проверить нулевую гипотезу Н0: М(X)=М(Y) о равенстве математических ожиданий двух нормальных генеральных совокупностей с неизвестными, но одинаковыми дисперсиями (в случае независимых малых выборок) при конкурирующей гипотезе Н1: М(X)¹М(Y), надо
1. Вычислить наблюдаемое значение критерия:
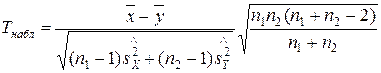 .
.
2. По таблице критических точек распределения Стьюдента (приложение 7) по заданному уровню значимости a (помещенному в верхней строке таблицы) и числу степеней свободы 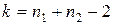 найти критическую точку tдвуст.кр(a, k).
найти критическую точку tдвуст.кр(a, k).
3. Если |Тнабл|< tдвуст.кр(a, k) – нет оснований отвергнуть нулевую гипотезу.
Если |Тнабл|> tдвуст.кр(a, k) – нулевую гипотезу отвергают.
Пример 6.2.6. По двум независимым выборкам, объемы которых соответственно равны n1=5 и n2=6, извлеченным из нормальных генеральных совокупностей Х и Y, найдены выборочные средние 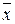 =3,3 и
=3,3 и 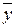 =2,48 и исправленные дисперсии
=2,48 и исправленные дисперсии 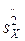 =0,25,
=0,25, 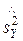 =0,108. При уровне значимости 0,05 проверить нулевую гипотезу Н0: М(X)=М(Y) о равенстве математических ожиданий при конкурирующей гипотезе Н1: М(X)¹М(Y).
=0,108. При уровне значимости 0,05 проверить нулевую гипотезу Н0: М(X)=М(Y) о равенстве математических ожиданий при конкурирующей гипотезе Н1: М(X)¹М(Y).
○ Так как выборочные дисперсии различны, проверим предварительно нулевую гипотезу о равенстве генеральных дисперсий, пользуясь критериием Фишера–Снедекора (см. 6.2.2.).
Найдем отношение большей исправленной дисперсии к меньшей:
Fнабл= 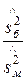
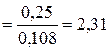 .
.
Дисперсия 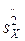 значительно больше дисперсии
значительно больше дисперсии 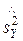 , поэтому в качестве конкурирующей гипотезы примем гипотезу Н1: D(X)>D(Y). В этом случае критическая область – правосторонняя.
, поэтому в качестве конкурирующей гипотезы примем гипотезу Н1: D(X)>D(Y). В этом случае критическая область – правосторонняя.
По таблице приложения 8, по уровню значимости a=0,05 и числам степеней свободы k1=5–1=4 и k2=6–1=5 находим критическую точку Fкр(0,05, 4, 5)=5,19.
Так как Fнабл<Fкр – нет оснований отвергнуть нулевую гипотезу о равенстве генеральных дисперсий.
Поскольку предположение о равенстве генеральных дисперсий выполняется, сравним средние.
Вычислим наблюдаемое значение критерия Стьюдента:
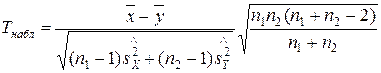 .
.
Подставив числовые значения величин, входящих в формулу, получим 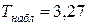 .
.
По условию, конкурирующая гипотеза имеет вид Н1: М(X)¹М(Y), поэтому критическая область – двусторонняя.
По таблице приложения 7, по уровню значимости a=0,05 и числам степеней свободы k=5+6–2=9 находим критическую точку tдвуст.кр(0,05, 9)=2,26.
Так как |Тнабл|> tдвуст.кр(a, k) – нулевую гипотезу о равенстве генеральных средних отвергаем. Другими словами, выборочные средние различаются значимо. ●
Случай 2. Для того, чтобы при заданном уровне значимости a проверить нулевую гипотезу Н0: М(X)=М(Y) о равенстве математических ожиданий двух нормальных генеральных совокупностей с неизвестными, но одинаковыми дисперсиями (в случае независимых малых выборок) при конкурирующей гипотезе Н1: М(X)>М(Y), надо
1. Вычислить наблюдаемое значение критерия:
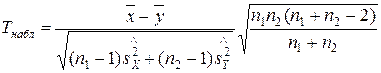 .
.
2. По таблице критических точек распределения Стьюдента (приложение 7) по заданному уровню значимости a (помещенному в нижней строке таблицы) и числу степеней свободы 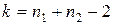 найти правостороннюю критическую точку tправост.кр(a, k).
найти правостороннюю критическую точку tправост.кр(a, k).
3. Если Тнабл< tправост.кр(a, k) – нет оснований отвергнуть нулевую гипотезу.
Если Тнабл> tправост.кр(a, k) – нулевую гипотезу отвергают.
Случай 3. Для того, чтобы при заданном уровне значимости a проверить нулевую гипотезу Н0: М(X)=М(Y) о равенстве математических ожиданий двух нормальных генеральных совокупностей с неизвестными, но одинаковыми дисперсиями (в случае независимых малых выборок) при конкурирующей гипотезе Н1: М(X)<М(Y), надо
1. Вычислить наблюдаемое значение критерия:
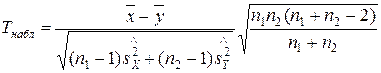 .
.
2. По таблице критических точек распределения Стьюдента (приложение 7) по заданному уровню значимости a (помещенному в верхней строке таблицы) и числу степеней свободы 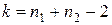 найти левостороннюю критическую точку:
найти левостороннюю критическую точку:
tлевост.кр(a, k)=– tправост.кр(a, k).
3. Если Тнабл>– tправост.кр(a, k) – нет оснований отвергнуть нулевую гипотезу.
Если Тнабл<– tправост.кр(a, k) – нулевую гипотезу отвергают.
6.2.5. Проверка гипотезы о законе распределения. Критерий c2 Пирсона
Проверка гипотезы о предполагаемом законе неизвестного распределения производится так же, как и проверка гипотезы о параметрах распределения, т.е. при помощи специально подобранной случайной величины – критерия согласия.
Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Рассмотрим один из таких критериев – c2-критерий К. Пирсона.
Схема применения критерия c2.
1) Определяется мера расхождения эмпирических и теоретических частот c2 по формуле:
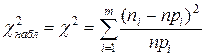 ,
,
где 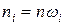 и
и 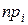 – соответственно эмпирические и теоретические частоты (
– соответственно эмпирические и теоретические частоты ( 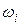 – статистические вероятности,
– статистические вероятности, 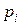 – гипотетические вероятности).
– гипотетические вероятности).
2) Для выбранного уровня значимости a по таблице c2-распределения (приложение 6.) находят критическое значение 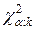 при числе степеней свободы k=m–r–1, где m – число интервалов эмпирического распределения (вариационного ряда); r – число параметров теоретического распределения, вычисленных по экспериментальным данным.
при числе степеней свободы k=m–r–1, где m – число интервалов эмпирического распределения (вариационного ряда); r – число параметров теоретического распределения, вычисленных по экспериментальным данным.
3) Если фактически наблюдаемое значение 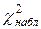 больше критического, т.е.
больше критического, т.е. 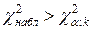 , то гипотеза Н0 (состоящая в том, что исследуемая случайная величина Х подчиняется определенному закону распределения) отвергается; если
, то гипотеза Н0 (состоящая в том, что исследуемая случайная величина Х подчиняется определенному закону распределения) отвергается; если 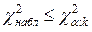 , то гипотеза Н0 не противоречит опытным данным.
, то гипотеза Н0 не противоречит опытным данным.
Примечание. Необходимо, чтобы в каждом интервале было достаточное количество наблюдений, по крайней мере, 5. Если в каком-нибудь интервале число наблюдений 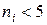 , то имеет смысл объединить соседние интервалы (при вычислении степеней свободы в качестве величины m берется соответственно уменьшенное число интервалов), чтобы в объединенных интервалах
, то имеет смысл объединить соседние интервалы (при вычислении степеней свободы в качестве величины m берется соответственно уменьшенное число интервалов), чтобы в объединенных интервалах 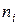 было не меньше 5.
было не меньше 5.
Пример 6.2.7.Имеются следующие статистические данные о числе вызовов специализированных бригад скорой помощи в час в некотором населенном пункте:
Число вызовов в час, 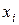 | 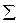 | |||||||||
Частота, 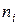 |
На уровне значимости a=0,05 проверить гипотезу о том, что случайная величина распределена по закону Пуассона.
○ 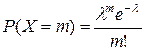 ; М(Х)=D(Х)=l.
; М(Х)=D(Х)=l.
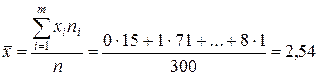 – несмещенная и состоятельная оценка l, т.е. l»
– несмещенная и состоятельная оценка l, т.е. l» 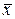 . Тогда
. Тогда 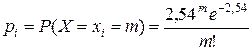 .
.
Для определения статистики 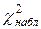 составим таблицу:
составим таблицу:
| i | xi=m | 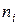 | 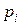 | 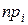 | 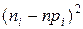 | 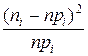 |
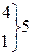 | 0,0789 0,2003 0,2544 0,2154 0,1368 0,0695 0,0294 0,0107 0,0034 | 23,7 60,1 76,3 64,6 41,0 20,9 8,8 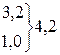 | 75,69 98,01 1,69 11,56 3,61 14,44 1,44 0,64 | 3,194 1,631 0,022 0,179 0,088 0,694 0,164 0,152 | ||
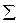 | 0,9988 | 299,6 | – | 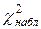 =6,12 =6,12 |
При расчете c2 объединяем последние два интервала, так как их частоты ( 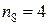 ,
, 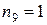 ) меньше 5.
) меньше 5.
Так как новое число интервалов (с учетом объединения двух последних) m=8, а закон Пуассона определяется r=1 параметром, то число степеней свободы k=m–r–1=8–1–1=6. По приложению 6. 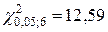 . Так как
. Так как 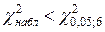 , то нет оснований отвергнуть гипотезу Н0 – она согласуется с опытными данными. ●
, то нет оснований отвергнуть гипотезу Н0 – она согласуется с опытными данными. ●
