Классификация показательных уравнений.
1. Уравнения, решаемые переходом к одному основанию.
Пример 18. Решить уравнение  .
.
Решение: Воспользуемся тем, что все основания степеней являются степенями числа 5:  .
.
2. Уравнения, решаемые переходом к одному показателю степени.
Эти уравнения решаются преобразованием исходного уравнения к виду  , которое использованием свойства пропорции приводится к простейшему.
, которое использованием свойства пропорции приводится к простейшему.
Пример 19. Решить уравнение: 
Решение:

 .
.
3. Уравнения, решаемые вынесением общего множителя за скобки.
Если в уравнении каждый показатель степени отличается от другого на некоторое число, то уравнения решаются вынесением за скобки степени с наименьшим показателем.
Пример 20. Решить уравнение  .
.
Решение: Вынесем в левой части уравнения степень с наименьшим показателем за скобки:


 .
.
Пример 21. Решить уравнение 
Решение: Сгруппируем отдельно в левой части уравнения слагаемые, содержащие степени с основанием 4, в правой части – с основанием 3, затем вынесем степени с наименьшим показателем за скобки:

 .
.
4. Уравнения, сводящиеся к квадратным (или кубическим) уравнениям.
К квадратному уравнению относительно новой переменной y сводятся уравнения:
а) вида  подстановкой
подстановкой  , при этом
, при этом  ;
;
б) вида  подстановкой
подстановкой  , при этом
, при этом  .
.
Пример 22. Решить уравнение  .
.
Решение: Сделаем замену переменной  и решим квадратное уравнение:
и решим квадратное уравнение:
 .
.
Ответ: 0; 1.
5. Однородные относительно показательных функций уравнения.
Уравнение вида  является однородным уравнением второй степени относительно неизвестных ax и bx . Такие уравнения сводятся предварительным делением обеих частей на
является однородным уравнением второй степени относительно неизвестных ax и bx . Такие уравнения сводятся предварительным делением обеих частей на  и последующей подстановкой
и последующей подстановкой  к квадратным уравнениям.
к квадратным уравнениям.
Пример 23. Решить уравнение  .
.
Решение: Разделим обе части уравнения на  :
:
 .
.
Положив  , получим квадратное уравнение
, получим квадратное уравнение  с корнями
с корнями  .
.
Теперь задача сводится к решению совокупности уравнений  . Из первого уравнения находим, что
. Из первого уравнения находим, что  . Второе уравнение не имеет корней, так как
. Второе уравнение не имеет корней, так как  при любых значения x.
при любых значения x.
Ответ: -1/2.
6. Рациональные относительно показательных функций уравнения.
Пример 24. Решить уравнение  .
.
Решение: Разделим числитель и знаменатель дроби на 3x и получим вместо двух – одну показательную функцию:

7. Уравнения вида  .
.
Такие уравнения с множеством допустимых значений (ОДЗ), определяемым условием  , логарифмированием обеих частей уравнения приводятся к равносильному уравнению
, логарифмированием обеих частей уравнения приводятся к равносильному уравнению  , которые в свою очередь равносильны совокупности двух уравнений
, которые в свою очередь равносильны совокупности двух уравнений  или
или  .
.
Пример 25. Решить уравнение:  .
.
Решение:
 .
.
Дидактический материал.
Решите уравнения:
1. 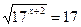 ; 2.
; 2. 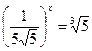 ; 3.
; 3. 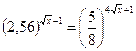 ;
;
4. 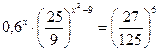 ; 5.
; 5. 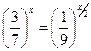 ; 6.
; 6. 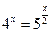 ;
;
7. 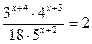 ; 8.
; 8. 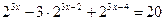 ;
;
9. 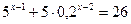 ; 10.
; 10. 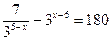 ; 11.
; 11. 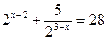 ;
;
12. 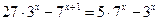 ; 13.
; 13. 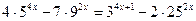 ;
;
14. 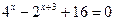 ; 15.
; 15. 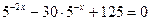 ;
;
16. 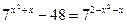 ; 17.
; 17. 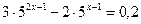 ;
;
18. 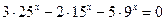 ; 19.
; 19. 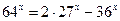 ;
;
20. 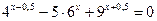 ; 21.
; 21. 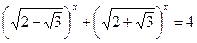 ;
;
22. 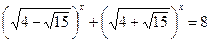 ; 23.
; 23. 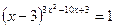 ;
;
24. 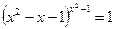 ; 25.
; 25. 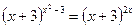 .
.
26. Найдите произведение корней уравнения 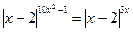 .
.
27. Найдите сумму корней уравнения 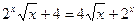 .
.
Найдите значение выражения:
28. 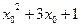 , где x0 – корень уравнения
, где x0 – корень уравнения 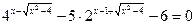 ;
;
29. 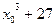 , где x0 – целый корень уравнения
, где x0 – целый корень уравнения 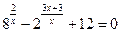 .
.
Решите уравнение:
30. 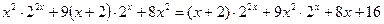 ;
;
31. 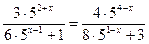 ; 32.
; 32. 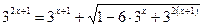 .
.
Ответы: 1. 0; 2. -2/9; 3. 1/36; 4. 0, 0.5; 5. 0; 6. 0; 7. -2; 8. 2; 9. 1, 3; 10. 8; 11. 5; 12. 1; 13. ¼; 14. 2; 15. -2, -1; 16. -2, 1; 17. 0; 18. 1; 19. 0; 20. -1, 0; 21. -2, 2; 22. -2, 2; 23. 4; 24. -1, 2; 25. -2, -1, 3; 26. -0.3; 27. 3; 28. 11; 29. 54; 30. -1, 0, 2, 3; 31. 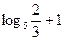 ; 32.
; 32. 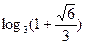 .
.
Тема №8.
Показательные неравенства.
1º. Неравенство, содержащее переменную в показателе степени, называется показательным неравенством.
2º. Решение показательных неравенств вида 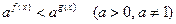 основано на следующих утверждениях:
основано на следующих утверждениях:
если 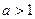 , то неравенство
, то неравенство 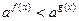 равносильно
равносильно 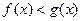 ;
;
если 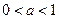 , то неравенство
, то неравенство 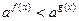 равносильно
равносильно 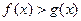 .
.
При решении показательных неравенств используют те же приемы, что и при решении показательных уравнений.
Пример 26. Решить неравенство 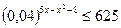 (методом перехода к одному основанию).
(методом перехода к одному основанию).
Решение: Так как 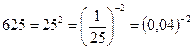 , то заданное неравенство можно записать в виде:
, то заданное неравенство можно записать в виде: 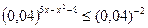 . Так как
. Так как 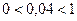 , то данное неравенство равносильно неравенству
, то данное неравенство равносильно неравенству 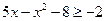 .
.
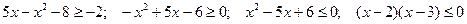 .
.
Решив последнее неравенство, получим 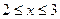 .
.
Ответ: 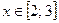 .
.
Пример 27. Решить неравенство: 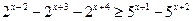 (методом вынесения общего множителя за скобки).
(методом вынесения общего множителя за скобки).
Решение: Вынесем за скобки в левой части неравенства 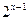 , в правой части неравенства
, в правой части неравенства 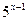 и разделим обе части неравенства на (-2), поменяв знак неравенства на противоположный:
и разделим обе части неравенства на (-2), поменяв знак неравенства на противоположный:
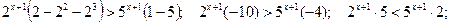
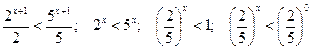 .
.
Так как 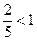 , то при переходе к неравенству показателей знак неравенства опять меняется на противоположный. Получаем
, то при переходе к неравенству показателей знак неравенства опять меняется на противоположный. Получаем 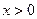 . Таким образом, множество всех решений данного неравенства есть интервал
. Таким образом, множество всех решений данного неравенства есть интервал 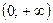 .
.
Ответ: 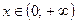 .
.
Пример 28. Решить неравенство 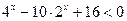 (методом введения новой переменной).
(методом введения новой переменной).
Решение: Пусть 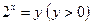 . Тогда данное неравенство примет вид:
. Тогда данное неравенство примет вид: 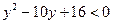 или
или 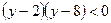 , решением которого является интервал
, решением которого является интервал 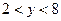 .
.
Отсюда 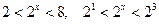 . Поскольку функция
. Поскольку функция 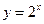 возрастает, то
возрастает, то 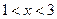 .
.
Ответ: 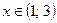 .
.
Дидактический материал.
Укажите множество решений неравенства:
1. 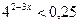 ; 2.
; 2. 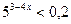 ; 3.
; 3. 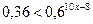 ;
;
4. 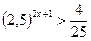 ; 5.
; 5. 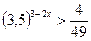 .
.
6. При каких значениях x точки графика функции 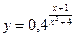 лежат ниже прямой
лежат ниже прямой 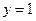 ?
?
7. При каких значениях x точки графика функции 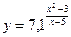 лежат не ниже прямой
лежат не ниже прямой 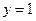 ?
?
Решите неравенство:
8. 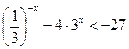 ; 9.
; 9. 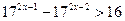 ; 10.
; 10. 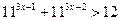 ;
;
11. 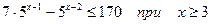 ; 12.
; 12. 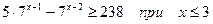 .
.
13. Укажите наибольшее целое решение неравенства 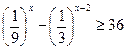 .
.
14. Найдите произведение наибольшего целого и наименьшего целого решений неравенства 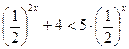 .
.
Решите неравенство:
15. 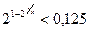 ; 16.
; 16.  ; 17.
; 17.  ;
;
18.  ; 19.
; 19.  ; 20.
; 20.  ;
;
21.  ; 22.
; 22.  ; 23.
; 23.  ;
;
24.  ; 25.
; 25.  ; 26.
; 26.  .
.
Найдите область определения функции:
27.  ; 28.
; 28.  .
.
29. Найдите множество значений аргумента, при которых значения каждой из функций больше 3:
 и
и  .
.
Ответы: 11. 3; 12. 3; 13. -3; 14. 1; 15. (0; 0,5); 16. [1,5; 5]; 17. (-1; 0)U(3; 4); 18. [-2; 2]; 19. (0; +∞); 20. (0; 1); 21. (3; +∞); 22. (-∞; 0)U(0,5; +∞); 23. (0; 1); 24. (-1; 1); 25. (0; 2]; 26. (3; 3,5)U (4; +∞); 27. (-∞; 3)U{5}; 28. [2; +∞); 29. (-∞; log5(5  -5)).
-5)).
Тема №9.
Логарифмы.
1º. Логарифмом числа b по основанию a (где  ) называется показатель степени, в которую надо возвести a, чтобы получить число b.
) называется показатель степени, в которую надо возвести a, чтобы получить число b.
Логарифм числа b по основанию a обозначается символом logab. В записи logab число a называют основанием логарифма, число b – логарифмируемым числом.
Равенство  означает, что
означает, что  .
.
2º. Основным логарифмическим тождеством называется равенство  , которое справедливо при
, которое справедливо при  .
.
Например,  .
.
3º. Логарифм по основанию 10 называется десятичным логарифмом и обозначается lg вместо log10. Логарифм по основанию e (e=2,712828…) называется натуральным логарифмом и обозначается ln вместо loge.
4º. Основные свойства логарифмов:
1)  ;
;
2)  ;
;
3)  (логарифм произведения), где
(логарифм произведения), где  ;
;
4)  (логарифм частного), где
(логарифм частного), где  ;
;
5)  (логарифм степени), где
(логарифм степени), где  ;
;
Замечание. Если b<0, а p – четное целое число, то справедлива формула:

6)  (формула перехода к другому основанию логарифма).
(формула перехода к другому основанию логарифма).
В частности,  .
.
Пример 29. Найти  .
.
Решение: Воспользуемся основным логарифмическим тождеством и свойством «логарифм степени».
 .
.
Пример 30. Вычислить  .
.
Решение: Для решения данного примера необходимо использовать все свойства логарифмов:
 .
.
Пример 31. Вычислить  .
.
Решение: Для решения данного примера используются все свойства логарифмов, а также основное логарифмическое тождество:

 .
.
Ответ: 19.
Пример 32. Найти  , если
, если  и
и  .
.
Решение: Разложим числа 168, 54, 24 и 12 на множители:
 . Полагая
. Полагая  и
и  , выразим через x и y все логарифмы, содержащиеся в условии:
, выразим через x и y все логарифмы, содержащиеся в условии:
 ;
;
 ;
;
 .
.
Согласно условию для определения x и y получаем систему уравнений:
 , решая которую находим
, решая которую находим  ,
,  .
.
Подставим найденные значения x и y в равенство для определения  , получим ответ:
, получим ответ:  .
.
5º. Логарифмирование – это преобразование, при котором логарифм выражения с переменными приводится к сумме или разности логарифмов переменных.
Потенцирование – это преобразование, обратное логарифмированию.
Пример 33. Дано  , где
, где  .
.
Найти выражение для x.
Решение: Потенцируя, получим:
 ,
,  .
.
Дидактический материал.
Вычислите:
1.  ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6.  ; 7.
; 7.  ;
;
8.  ; 9.
; 9.  ; 10.
; 10.  ;
;
11.  ; 12.
; 12.  .
.
13. Прологарифмируйте по основанию 3 выражение  .
.
14. Прологарифмируйте по основанию 5 выражение  .
.
15. Прологарифмируйте по основанию 4 выражение  .
.
16. Вычислите x, если  .
.
17. Вычислите x, если  .
.
Вычислите значение выражения:
18.  при
при  ;
;
19.  при
при  ;
;
20.  при
при  ;
;
21.  при
при  .
.
Упростите выражение:
22.  ; 23.
; 23.  ;
;
24.  ; 25.
; 25.  .
.
26. Известно, что  . Найдите
. Найдите  .
.
27. Найдите значение выражения  , если
, если  .
.
28. Найдите значение выражения  , если
, если  .
.
29. Найдите значение выражения  , если
, если  .
.
30. Найдите значение выражения  , если
, если  .
.
Найдите значение функции:
31.  при
при  ;
;
32.  при
при  .
.
Тема №10.
Преобразование тригонометрических выражений.
1º. На плоскости xOy рассмотрим окружность с центром в начале координат и радиусом, равным 1. На единичной окружности отметим точку A(1;0). Радиус OA называют начальным радиусом. При повороте начального радиуса на угол α около центра О точка А(1;0) перейдет в некоторую точку М(x;y). Заметим, что поворот можно осуществить по часовой стрелки (угол поворота положителен) или против часовой стрелки (угол поворота отрицателен).
 Косинусом угла α называется абсцисса точки М:
Косинусом угла α называется абсцисса точки М:  .
.
Синусом угла α называется ордината точки М:  .
.
Тангенсом угла α называется отношение ординаты точки М к ее абсциссе:  .
.
Котангенсом угла α называется отношение абсциссы точки М к ее ординате:  .
.
 являются тригонометрическими функциями аргумента α.
являются тригонометрическими функциями аргумента α.
2º. Единицами измерения величины угла являются градус и радиан.
Если начальный радиус окружности совершит один полный оборот, то получится угол, равный 360˚ или 2π радиан.
Связь между градусной и радианной мерами измерения угла:  рад.
рад.
Из этой формулы следует:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  и т.д.
и т.д.
3º. Свойства тригонометрических функций:
Функции  - нечетные функции:
- нечетные функции:
 .
.
Функция  - четная:
- четная:  .
.
Функции  - периодические с наименьшим периодом 2π:
- периодические с наименьшим периодом 2π:
 .
.
Функции  - периодические с наименьшим периодом π:
- периодические с наименьшим периодом π:
 .
.
4º. Основное тригонометрическое тождество.
Согласно теореме Пифагора (“в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы”) координаты любой точки М(x;y) единичной окружности удовлетворяют уравнению:  . Отсюда:
. Отсюда:
 где
где  (10.1)
(10.1)
Из этой формулы следует:
а)  ; б)
; б)  .
.
5º. Основные соотношения между тригонометрическими функциями:
 , (10.2)
, (10.2)
 , (10.3)
, (10.3)
 , (10.4)
, (10.4)
 , (10.5)
, (10.5)
 . (10.6)
. (10.6)
6º. Формулы сложения аргументов:
 , (10.7)
, (10.7)
 , (10.8)
, (10.8)
 . (10.9)
. (10.9)
7º. Формулы двойного аргумента:
 , (10.10)
, (10.10)
 , (10.11)
, (10.11)
 . (10.12)
. (10.12)
8º. Формулы понижения степени синуса и косинуса:
 . (10.13)(10.14)
. (10.13)(10.14)
9º. Преобразование суммы и разности одноименных тригонометрических функций в произведение:
 , (10.15)
, (10.15)
 , (10.16)
, (10.16)
 , (10.17)
, (10.17)
 . (10.18)
. (10.18)
10º. Преобразование произведения тригонометрических функций в сумму:
 , (10.19)
, (10.19)
 , (10.20)
, (10.20)
 . (10.21)
. (10.21)
11º. Выражение тригонометрических функций через тангенс половинного аргумента.
При доказательстве тождеств, решении тригонометрических уравнений и т.п. часто возникает необходимость выразить все 4 тригонометрические функции через какую-нибудь одну функцию f(x). Для этого пользуются следующими формулами:
а)  , (10.22)
, (10.22)
б)  , (10.23)
, (10.23)
в)  . (10.24)
. (10.24)
12º. Формулы приведения. Это соотношения, при помощи которых значения тригонометрических функций аргументов  выражают через тригонометрические функции угла α. Все формулы приведения можно свести в следующую таблицу:
выражают через тригонометрические функции угла α. Все формулы приведения можно свести в следующую таблицу:
| Аргумент t Функция |  |  |  |  |  |  |  |  |
| sin t | cos α | cos α | sin α | - sin α | -cos α | -cos α | -sin α | sin α |
| cos t | sin α | -sin α | -cos α | -cos α | -sin α | sin α | cos α | cos α |
| tg t | ctg α | -ctg α | -tg α | tg α | ctg α | -ctg α | -tg α | tg α |
| ctg t | tg α | -tg α | -ctg α | ctg α | tg α | -tg α | -ctg α | ctg α |
Пример 34. Найдите  , если
, если  .
.
Решение:  . По формуле (10.6)
. По формуле (10.6) 
 . Так как α находится в 3-ей четверти, то
. Так как α находится в 3-ей четверти, то  и, следовательно,
и, следовательно,  . Ответ:
. Ответ:  .
.
Пример 35. Вычислить значение выражения  , если
, если  .
.
Решение: Используем формулу (10.10), а затем числитель и знаменатель дроби разделим на  . Тогда:
. Тогда:


Ответ: 9,25.
Пример 36. Доказать тождество:  .
.
Решение: Используя формулы (10.15), (10.16), получим:

 .
.
Пример 37. Вычислить  , если
, если  .
.
Решение: Выразив  и
и  через
через  по формулам (10.22), (10.23), получим:
по формулам (10.22), (10.23), получим:
 .
.
Ответ: ¼.
Пример 38. Упростить выражение:  .
.
Решение: Воспользуемся свойствами четности и нечетности тригонометрических функций, а также выделим период в аргументе функций и исключим его, опираясь на свойство периодичности функций:
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Получаем: 
Далее используем формулы приведения:
 .
.
Ответ: -1.
Пример 39. Найти  .
.
Решение: Воспользуемся формулой приведения  и определением котангенса:
и определением котангенса:
 .
.
Поскольку угол  находится в 4-ой четверти
находится в 4-ой четверти  , то
, то  . Получаем:
. Получаем:
 .
.
Дидактический материал.
Найдите значение выражения:
-
 , если
, если  ;
; -
 , если
, если  ;
; -
 , если
, если  ;
; -
 , если
, если  ;
; -
 , если
, если  , а α и β – углы I четверти;
, а α и β – углы I четверти; -
 , если
, если  ; а α и β – углы I четверти;
; а α и β – углы I четверти; -
 , если
, если  ;
; -
 , если
, если  .
.
Вычислите:
-
 , если
, если  ;
; -
 , если
, если  ;
; -
 , если
, если  .
.
Упростите выражение:
-
 ; 13.
; 13.  ;
;
-
 ; 15.
; 15.  ;
;
-
 ;
; -
 ; 18.
; 18.  ;
;
-
 .
.
Преобразуйте в произведение:
-
 ;
; -
 .
.
Найдите значение выражения:
-
 ; 23.
; 23.  ;
;
-
 ; 25.
; 25.  ; 26.
; 26.  .
.
Ответы: 1. 0; 2. 5,92; 3. 10; 4. 3; 5. 5,2; 6. 6; 7. 3; 8. 3; 9. 1,24; 10. -10; 11. 7/25; 12. 1; 13. 2; 14. 0; 15. 0; 16. 2; 17. -1; 18. 2; 19. -1; 20.  ; 21.
; 21.  ; 22.
; 22.  ; 23.
; 23.  ; 24. 21; 25. 24; 26. 26.
; 24. 21; 25. 24; 26. 26.
Тема №11.
