Решение линейных и квадратных неравенств.
1º. Решить неравенство с одной переменной – значит найти множество значений переменной, при которых это неравенство является верным. Элементы этого множества называются решениями неравенства.
Два неравенства, содержащие одну и ту же переменную, называются равносильными, если множества решений этих неравенств совпадают. Равносильность неравенств обозначается так: 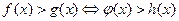 .
.
2º. Линейным неравенством называется неравенство вида 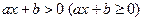 , где
, где 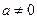 .
.
Если a > 0, то 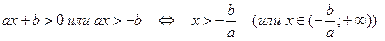 .
.
Если a < 0, то 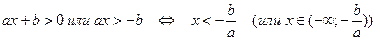 .
.
Пример 9. Решить неравенство, сводящееся к линейному:
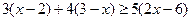 .
.
Решение: Раскрыв скобки, получим:
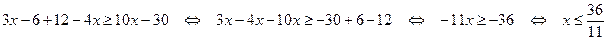 .
.
Ответ: 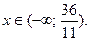
3º. Квадратным неравенством называется неравенство вида 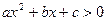 (или
(или 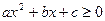 ), где а ≠ 0.
), где а ≠ 0.
При решении квадратного неравенства 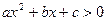 в зависимости от знака дискриминанта
в зависимости от знака дискриминанта 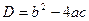 могут представиться 3 варианта:
могут представиться 3 варианта:
1) Если D < 0, то график квадратного трехчлена 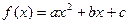 не пересекает ось Ох и лежит выше этой оси при a > 0 и ниже ее при a < 0. В первом случае множество решений неравенства есть вся числовая прямая, а во втором – пустое множество.
не пересекает ось Ох и лежит выше этой оси при a > 0 и ниже ее при a < 0. В первом случае множество решений неравенства есть вся числовая прямая, а во втором – пустое множество.
2) Если D > 0, то график квадратного трехчлена пересекает ось Ох в точках х1 и х2 (x1 < x2), являющихся корнями уравнения 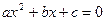 . Эти точки разбивают числовую прямую на три промежутка (-∞; x1), (x1; x2), (x2; +∞). Если a > 0, то решением неравенства является множество
. Эти точки разбивают числовую прямую на три промежутка (-∞; x1), (x1; x2), (x2; +∞). Если a > 0, то решением неравенства является множество 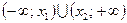 . Если a < 0, то решением неравенства является множество (x1; x2).
. Если a < 0, то решением неравенства является множество (x1; x2).
3) Если D = 0, то график квадратного трехчлена касается оси Ох в точке х1, являющейся единственным корнем уравнения 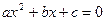 . При a < 0 решением неравенства будет пустое множество, при a > 0 – множество
. При a < 0 решением неравенства будет пустое множество, при a > 0 – множество 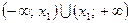 .
.
Пример 10. Решить неравенство 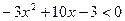 .
.
Решение: Рассмотрим функцию 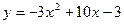 . Графиком этой функции является парабола, ветви которой направлены вниз, так как a = -3 < 0.
. Графиком этой функции является парабола, ветви которой направлены вниз, так как a = -3 < 0.
Решим уравнение 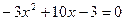 или
или 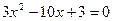 . Корни этого уравнения
. Корни этого уравнения 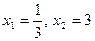 . Изобразив схематически параболу
. Изобразив схематически параболу 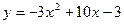 , найдем, что y < 0 в каждом из промежутков (-∞; 1/3), (3; +∞).
, найдем, что y < 0 в каждом из промежутков (-∞; 1/3), (3; +∞).
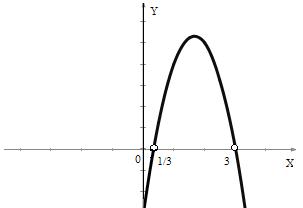
Ответ: 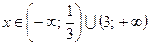 .
.
Метод интервалов.
1º. Если дискриминант квадратного трехчлена D > 0 или D = 0, то квадратное неравенство 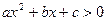 можно переписать в виде
можно переписать в виде 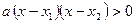 или
или 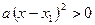 , где x1 и x2 – корни квадратного трехчлена, и использовать для его решения метод интервалов.
, где x1 и x2 – корни квадратного трехчлена, и использовать для его решения метод интервалов.
2º. Для решения любых алгебраических уравнений
вида (1) 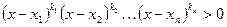 или вида (2)
или вида (2) 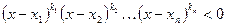 , где x1, x2, …, xn – действительные числа, удовлетворяющие условию x1 < x2 < …< xn, а k1, k2, …, kn – натуральные числа, применим обобщенный метод интервалов.
, где x1, x2, …, xn – действительные числа, удовлетворяющие условию x1 < x2 < …< xn, а k1, k2, …, kn – натуральные числа, применим обобщенный метод интервалов.
Суть его состоит в следующем: на координатной оси отмечают числа x1, x2, …, xn, в промежутке справа от xn ставят знак +,
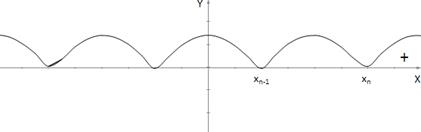
затем, двигаясь справа налево, при переходе через очередную точку xi меняют знак, если ki - нечетное число и сохраняют знак, если ki - четное число. Тогда множеством решений неравенства (1) будет объединение промежутков, в каждом из которых поставлен знак +, а множеством решений неравенства (2) будет объединение промежутков, в каждом из которых поставлен знак – .
Замечание. Обобщенный метод интервалов справедлив и для целых рациональных неравенств P(x) > 0 или Q(x) ≥ 0, и для дробно-рациональных неравенств 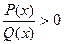 или
или 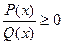 , причем последние равносильны неравенству
, причем последние равносильны неравенству 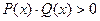 и системе
и системе 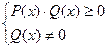 соответственно, где P(x), Q(x) – некоторые многочлены.
соответственно, где P(x), Q(x) – некоторые многочлены.
Пример 11. Решить неравенство 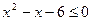 .
.
Решение: Находим корни квадратного трехчлена 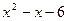 :
:
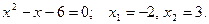 Данное неравенство равносильно следующему неравенству:
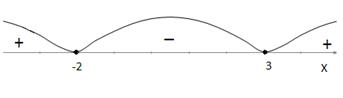
Данное неравенство равносильно следующему неравенству: 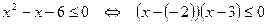 . Применяя метод интервалов к последнему неравенству, получим множество всех решений неравенства – отрезок [-2; 3].
. Применяя метод интервалов к последнему неравенству, получим множество всех решений неравенства – отрезок [-2; 3].
Ответ: 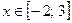 .
.
Пример 12. Решить неравенство 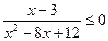 .
.
Решение:
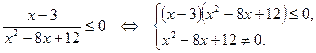
Находим корни числителя и знаменателя: 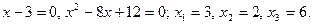
Указанная система равносильна следующей системе: 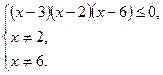
Нанесем найденные корни на числовую прямую. В интервалах справа налево расставим знаки плюс и минус.
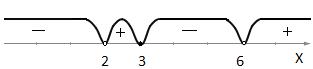
Множеством всех решений данного неравенства является объединение промежутков, в которых поставлен знак минус.
Ответ: 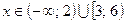 .
.
Дидактический материал.
Решите неравенства:
1. 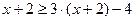 ; 2.
; 2. 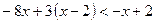 ;
;
3. 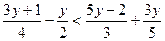 ; 4.
; 4. 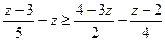 .
.
Решите системы неравенств:
5. 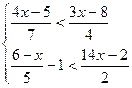 ; 6.
; 6. 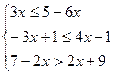 .
.
Найдите целые решения системы неравенств:
7. 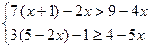 ; 8.
; 8. 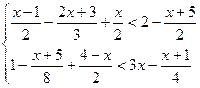 .
.
Решите неравенства:
9. 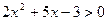 ; 10.
; 10. 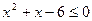 ; 11.
; 11. 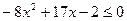 ;
;
12. 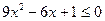 ; 13.
; 13. 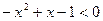 ;
;
14. 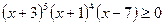 ; 15.
; 15. 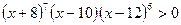 ;
;
16. 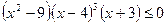 ; 17.
; 17. 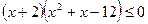 ;
;
18. 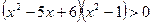 ; 19.
; 19. 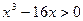 ;
;
20. 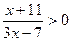 ; 21.
; 21. 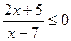 ; 22.
; 22. 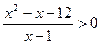 ;
;
23. 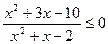 ; 24.
; 24. 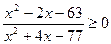 ;
;
25. 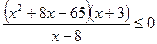 ; 26.
; 26. 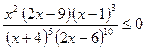 ;
;
27. 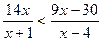 ; 28.
; 28. 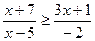 ; 29.
; 29. 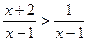 ;
;
30. 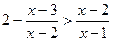 ; 31.
; 31. 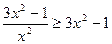 ; 32.
; 32. 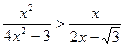 .
.
Тема №5.
