Квадратичная функция, ее график.
1º. Функция, заданная формулой 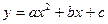 , где x, y – переменные, a, b, c – действительные числа, причем а ≠ 0, называется квадратичной.
, где x, y – переменные, a, b, c – действительные числа, причем а ≠ 0, называется квадратичной.
2º. Графиком функции 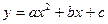 является парабола – кривая, симметричная относительно прямой
является парабола – кривая, симметричная относительно прямой 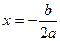 , проходящей через вершину параболы.
, проходящей через вершину параболы.
Координаты вершины параболы определяются по формулам:
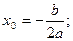
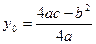 .
.
Если квадратичную функцию 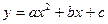 путем выделения полного квадрата привести к виду
путем выделения полного квадрата привести к виду 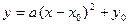 , то точка (x0; y0) – вершина параболы.
, то точка (x0; y0) – вершина параболы.
График квадратичной функции 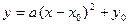 получается из графика функции
получается из графика функции 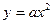 с помощью параллельного переноса.
с помощью параллельного переноса.
3º. Если коэффициент a > 0, ветви параболы направлены вверх, если a < 0 – вниз.
При 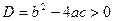 парабола пересекает ось абсцисс в двух точках, при D=0 – в одной (т.е. касается оси Ох), при D<0 - парабола не пересекает ось абсцисс.
парабола пересекает ось абсцисс в двух точках, при D=0 – в одной (т.е. касается оси Ох), при D<0 - парабола не пересекает ось абсцисс.
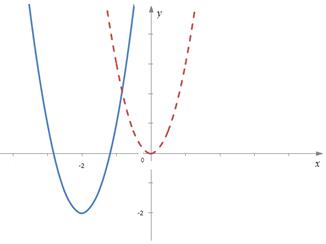
Пример 3. Построим график функции 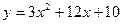 .
.
Выполним следующие преобразования (называемые «выделением полного квадрата»): 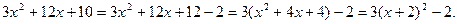
График функции 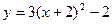 получается из графика функции
получается из графика функции 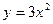 параллельным переносом на 2 единицы влево и на две единицы вниз.
параллельным переносом на 2 единицы влево и на две единицы вниз.
Уравнения, содержащие переменную под знаком модуля.
1º. Модуль (абсолютная величина) числа а определяется следующим образом:
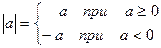 .
.
Геометрический смысл модуля: |a| есть расстояние от точки числовой оси, изображающей данное число а, до начала отсчета - точки О, а |x-a| есть расстояние между точками числовой оси, соответствующими числам х и а.
2º. Уравнения вида 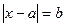 можно решать геометрически.
можно решать геометрически.
Рассмотрим аналитические способы решения уравнений, содержащих переменную под знаком модуля, на примерах.
При решении уравнений важно уметь в соответствии с определением модуля освободиться от вертикальных скобок.
Например, 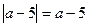 , если a ≥ 5;
, если a ≥ 5;
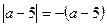 , если a < 5.
, если a < 5.
Пример 4. Решим уравнение 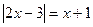 , используя определение модуля числа.
, используя определение модуля числа.
Решение: Уравнение имеет решение, если x+1≥0, т.е. x≥-1.
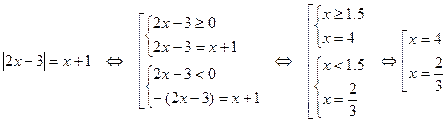 .
.
Условие x≥-1 выполняется в обоих случаях.
Ответ: 4; 2/3.
Пример 5. Решим уравнение 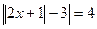 , используя свойство модулей («модули противоположных чисел равны»).
, используя свойство модулей («модули противоположных чисел равны»).
Решение:
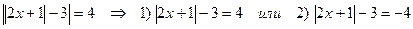 .
.
1) |2x+1|=7 => 2x+1=7 или 2x+1=-7 => x=3 или x=-4
2) |2x+1|-3=-4 => |2x+1|=-1 – нет решений.
Ответ: 3; -4.
Пример 6. Решим уравнение 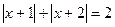 , рассматривая решения на интервалах.
, рассматривая решения на интервалах.
Решение: Найдем нули модулей, т.е. такие значения x, при которых 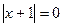 и
и 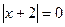 :
: 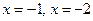 .
.
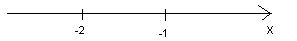
Рассмотрим уравнение на интервалах (-∞; -2), [-2; -1), [-1; +∞).
а) Для 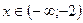 уравнение примет вид:
уравнение примет вид:
-(x+1)-(x+2)=2; -x-1-x-2=2; -2x=5; x=-2,5; 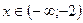 => x=-2,5 – корень уравнения.
=> x=-2,5 – корень уравнения.
б) Для 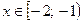 уравнение примет вид:
уравнение примет вид:
-(x+1)+(x+2)=2; -x-1+x+2=2; 0·x=1- нет корней.
в) Для 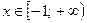 уравнение примет вид:
уравнение примет вид:
x+1+x+2=2; 2x=-1; x=-0,5; 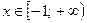 => x=-0,5 – корень уравнения.
=> x=-0,5 – корень уравнения.
Ответ: -2,5; -0,5.
Дидактический материал.
Решите уравнения, сводящиеся к линейным:
1. 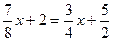 ; 2.
; 2. 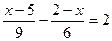 ; 3.
; 3. 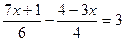 ;
;
4. 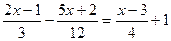 ; 5.
; 5. 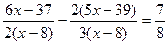 ;
;
6. 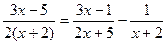 ; 7.
; 7. 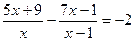 ;
;
8. 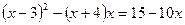 ; 9.
; 9. 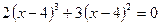 ;
;
10. 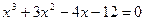 ; 11.
; 11. 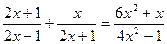 .
.
Решите квадратные уравнения:
12. 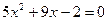 ; 13.
; 13. 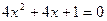 ;
;
14. 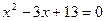 ; 15.
; 15. 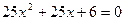 ;
;
16. 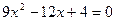 .
.
Разложите на линейные множители:
17. 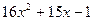 ; 18.
; 18. 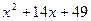 ; 19.
; 19. 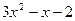 ;
;
20. 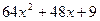 ; 21.
; 21. 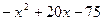 .
.
Сократите дроби:
22. 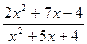 ; 23.
; 23. 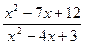 ; 24.
; 24. 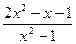 ;
;
25. 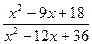 ; 26.
; 26. 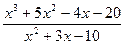 ; 27.
; 27. 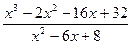 .
.
Упростите выражение:
28. 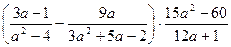 ; 29.
; 29. 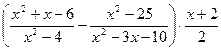 .
.
Найдите среднее арифметическое всех действительных корней уравнения:
30. 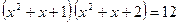 ; 31.
; 31. 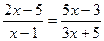 ;
;
32. 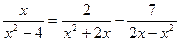 ; 33.
; 33. 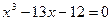 ;
;
34. 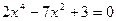 ; 35.
; 35. 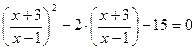 ;
;
36. 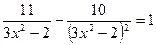 .
.
Найдите расстояние от вершины параболы до точки М:
37. 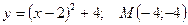 ; 38.
; 38. 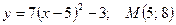 ;
;
39. 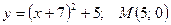 ; 39.
; 39. 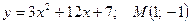 .
.
Постройте график функции:
40. 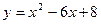 ; 41.
; 41. 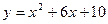 ; 42.
; 42. 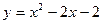 ;
;
43. 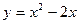 ; 44.
; 44. 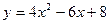 ; 45.
; 45. 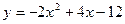 ;
;
46. 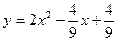 ; 47.
; 47. 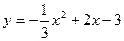 ; 48.
; 48. 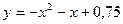 ;
;
49. 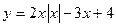 ; 50.
; 50. 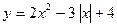 ; 51.
; 51. 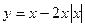 .
.
52. По графику квадратичной функции определить знаки ее коэффициентов и их суммы:
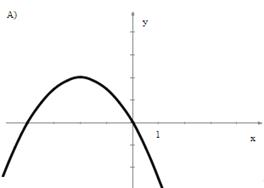
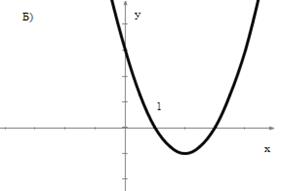
Найдите рациональные корни уравнения:
53. 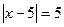 ; 54.
; 54. 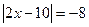 ; 55.
; 55. 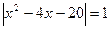 ;
;
56. 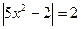 ; 57.
; 57. 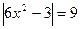 ; 58.
; 58. 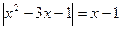 ;
;
59. 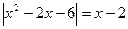 ; 60.
; 60. 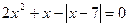 ; 61.
; 61. 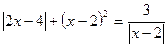 .
.
Решите уравнения:
62. 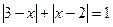 ; 63.
; 63. 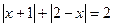 ; 64.
; 64. 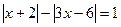 ;
;
65. 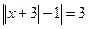 ; 66.
; 66. 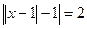 ; 67.
; 67. 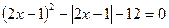 ;
;
68. 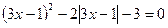 ; 69.
; 69. 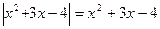 ;
;
70. 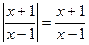 ; 71.
; 71. 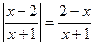 ; 72.
; 72. 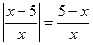 .
.
Тема №3.
Степени и корни.
