Линейная алгебра и аналитическая геометрия
Основы линейной алгебры
1. Матрицы. Типы матриц.
2. Операции над матрицами.
3. Определители. Вычисление определителей 2-го и 3-го порядка.
4. Миноры и алгебраические дополнения, теорема Лапласа.
5. Свойства определителей.
6. Обратная матрица, существование и вычисление.
Системы линейных уравнений
7. Система линейных уравнений, ее решения
8. Nтипы систем линейных уравнений. Матричная запись системы линейных уравнений.
9. Метод обратной матрицы.
10. Теорема Крамера, формулы Крамера.
11. Ранг матрицы, элементарные преобразования матриц, расширенная матрица.
12. Общая теория систем линейных уравнений, теорема Кронекера-Капелли.
13. Метод последовательного исключения переменных Гаусса.
Основы аналитической геометрии
14. Понятие вектора. Операции над векторами.
15. Линейная зависимость векторов, базис.
16. Скалярное произведение векторов.
17. Векторное произведение векторов.
18. Смешанное произведение векторов.
19. Уравнения прямой на плоскости.
20. Уравнения плоскости в пространстве.
21. Плоскость и прямая в пространстве.
22. Кривые второго порядка: эллипс, гипербола, парабола.
23. Инварианты кривых второго порядка
Рекомендуемая литература
1. Канатников А.Н., Крищенко А.П. Линейная алгебра. М., Изд. МГТУ им. Н.Э. Баумана, 1999.
2. Канатников А.Н., Крищенко А.П. Аналитическая геометрия. М., Изд. МГТУ им. Н.Э. Баумана, 1999.
3. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М., Наука, 1984.
4. Ильин В.А., Позняк Э.Г. Линейная алгебра. М., Наука, 1988.
5. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. М., Наука, 1988.
6. Сборник задач по математике для втузов. Ч. 1. Под общ. ред. А.В. Ефимова и Б.П.Демидовича. М., Наука, 1993.
7. Проскуряков И.В. Сборник задач по линейной алгебре. М., Наука, 1974.
8. Куликов Л.Я., Москаленко А.И., Фомин А.А. Сборник задач по алгебре и теории чисел. М., Просвещение, 1993.
Контрольное задание
(№ варианта равен последней цифре номера зачётной книжки, вар. 10 соответствует цифре 0)
1 задание. Вычислить определитель матрицы 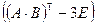 :
:
I вар. 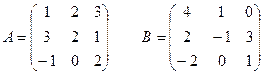 | II вар. 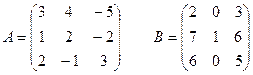 |
III вар. 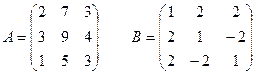 | IV вар. 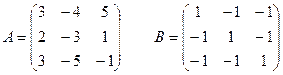 |
V вар. 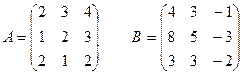 | VI вар. 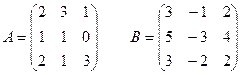 |
VII вар. 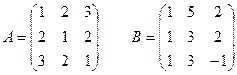 | VIII вар. 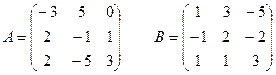 |
IX вар. 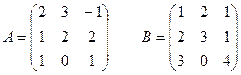 | X вар. 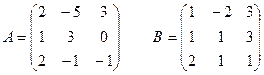 |
2 задание. Найти обратную матрицу
I вар. 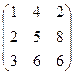 | II вар. 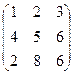 | III вар. 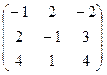 | IV вар. 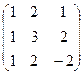 | V вар. 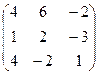 |
VI вар. 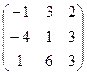 | VII вар. 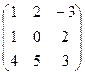 | VIII вар. 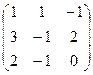 | IX вар. 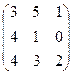 | X вар. 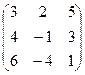 |
3 задание. Решить систему линейных уравнений методом Гаусса
I вар. 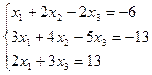 | II вар. 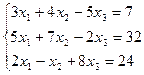 |
III вар. 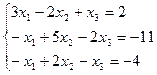 | IV вар. 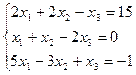 |
V вар. 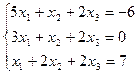 | VI вар. 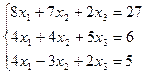 |
VII вар. 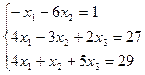 | VIII вар. 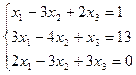 |
IX вар. 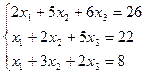 | X вар. 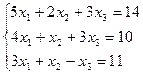 |
4 задание.Даны три вектора p = {3; -2; 1}, q = {-1; 1; -2}, r = {2; 1; -3}
Найти разложение вектора c по базису p, q, r.
| Вариант 1-3 | Вариант 4-6 | Вариант 7-10 |
c = {11; -6; 5} c = {9; -6; 4} c = {-7; -7; 5}
5 задание. Составить каноническое уравнение прямой
| Вариант 1-3 | Вариант 4-6 | Вариант 7-10 |
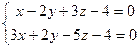
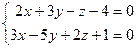
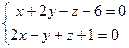
6 задание.При каких значениях m и n уравнение определяет:
1. Центральную линию;
2. Линию без центра;
3. Линию, имеющую бесконечно много центров.
| Вариант 1-3 | x2 + 6xy + my2 + 3x + ny – 4 = 0 |
| Вариант 4-6 | mx2 + 12xy + 9y2 + 4x + ny – 13 = 0 |
| Вариант 7-10 | 5x2 + 14xy + my2 + 20x + ny – 18 = 0 |
Семестр
Теория вероятностей
