Тема 4. Декартово произведение множеств
Теоретический материал
Обозначения:
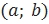– упорядоченная пара, образованная из элементов 
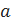и 
;
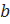А×В – декартово произведение множеств A и B;
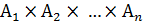– декартово произведение множеств 
;
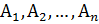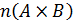– количество элементов в декартовом произведении множеств A и B;
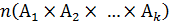– количество элементов в декартовом произведении множеств 
.
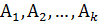Элемент 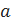– первая координата (компонента) пары; элемент 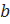– вторая координата (компонента) пары.
Декартово произведение множеств А и В (А×В) – множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента – множеству В.
Кортеж – упорядоченный набор 3 и более элементов.
Декартово произведение множеств 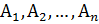( 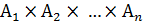) – множество всех кортежей длины n, первая компонента которых принадлежит множеству А1, вторая – множеству А2, …, n-я – множеству Аn.
Способы представления декартова произведения множеств:
а) перечисление элементов;
б) граф;
в) таблица;
г) на координатной плоскости.
Число элементов в декартовом произведении конечных множеств:
Два множества: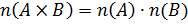 
.
k множеств: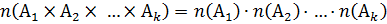 
.
Задания
1. Найти декартово произведение множеств:
а)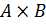 
и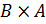 
: 
, 
;
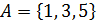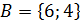б)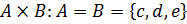 
;
в)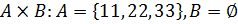 
;
г)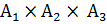 
: 
, 
.
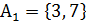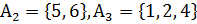2. Представьте в виде графа и таблицы декартово произведение множеств ,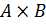 
, 
.
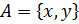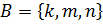Таблица:
Граф:
3. Изобразите на координатной плоскости декартово произведение 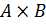, если:
а) ,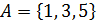 
;
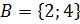б) ,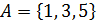 
;
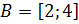в)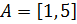 
, ;
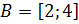г)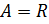 
, .
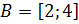4. Сколько чисел можно составить из цифр 7, 8, 9, если:
а) числа двузначные, цифры в записи числа не повторяются;
б) числа двузначные, цифры в записи числа могут повторяться;
в) числа трехзначные, цифры в записи числа не повторяются;
г) числа трехзначные, цифры в записи числа могут повторяться.
5. Сколько чисел можно составить из цифр 5, 4, 0, если:
а) числа двузначные, цифры в записи числа не повторяются;
б) числа двузначные, цифры в записи числа могут повторяться;
в) числа трехзначные, цифры в записи числа не повторяются;
г) числа трехзначные, цифры в записи числа могут повторяться.
6. Запишите множество дробей, числителем которых являются числа из множества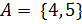 
, а знаменателем – числа из множества 
.
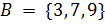7. 3апишите различные двузначные числа, используя цифры 1, 3, 5, 7. Сколько среди них чисел, запись которых начинается с цифры 5? Переформулируйте эту задачу, используя понятие декартова произведения множеств.
Тема 5. Математические понятия
Теоретический материал
Объем понятия – это множество всех объектов, обозначаемых одним термином.
Содержание понятия – это множество всех существенных свойств объекта, отраженных в этом понятии.
Если увеличивается объем понятия, то уменьшается его содержание, и наоборот.
Пусть заданы два понятия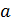 
и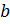 
, имеющие объемы соответственно 
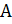и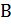 
. Если 
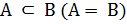, то говорят, что понятие 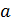– видовое по отношению к понятию 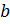, а понятие 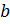– родовое по отношению к .
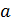Если А = В, то говорят, что понятия 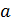и 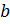тождественны.
Операции с понятиями:
1. Обобщение понятия.
2. Ограничение понятия.
3. Деление понятия.
4. Определение понятия.
Определение понятия через род и видовое отличие
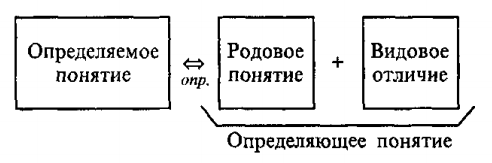
Правила определения понятий:
1. Соразмерность определения.
2. Отсутствие порочного круга в определении.
3. Ясность определения.
Неявные определения:
1. Контекстуальные.
2. Остенсивные.
Задания
1. Выберите пары понятий, которые находятся в отношении рода и вида:
а) многоугольник и треугольник;
б) угол и острый угол;
в) луч и прямая;
г) ромб и квадрат;
д) круг и окружность;
е) трехзначное число и двухзначное число.
_____________________________________________________________
_____________________________________________________________
2. Назовите пять существенных свойств понятия «равнобедренный треугольник» и изобразите с помощью кругов Эйлера отношение между объемом данного понятия и объемом понятия «остроугольный треугольник». [3, c.25]
Находятся ли понятия «остроугольный треугольник» и «равнобедренный треугольник» в отношении рода и вида?
Свойства:
1. ___________________________________________________________
_____________________________________________________________
_____________________________________________________________
2. ___________________________________________________________
_____________________________________________________________
_____________________________________________________________
3. ___________________________________________________________
_____________________________________________________________
_____________________________________________________________
4. ___________________________________________________________
_____________________________________________________________
_____________________________________________________________
5. ___________________________________________________________
_____________________________________________________________
_____________________________________________________________
3. Выделите в определении «Высотой треугольника, проведенной из данной вершины, называют отрезок перпендикуляра между этой вершиной и прямой, содержащей противолежащую сторону» определяемое и определяющее понятие, родовое понятие (по отношению к определяемому) и видовое отличие.
Определяемое понятие:_________________________________________
_____________________________________________________________
_____________________________________________________________
Определяющее понятие:________________________________________
_____________________________________________________________
_____________________________________________________________
Родовое понятие:______________________________________________
_____________________________________________________________
_____________________________________________________________
Видовое отличие:______________________________________________
_____________________________________________________________
_____________________________________________________________
4. Сформулируйте понятие прямоугольника, используя в качестве родового понятия не менее двух различных понятий. Какие видовые отличия необходимо указать в каждом случае?
а) Определение:_______________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
Родовое понятие:______________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
Видовое отличие:______________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
б) Определение:_______________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
Родовое понятие:______________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
Видовое отличие:______________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
в) Определение:________________ _______________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
Родовое понятие:______________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
Видовое отличие:______________________________________________
_____________________________________________________________
_____________________________________________________________
_____________________________________________________________
5. Какой вид определения понятия используется при введении понятий «четырехугольники» и «прямоугольники» в начальной школе (Дорофеев, Г.В., Миракова, Т.Н. Математика. 1 класс: учебник. В 2 ч. Ч.1, с. 64)?
____________________________________________________________
____________________________________________________________
____________________________________________________________
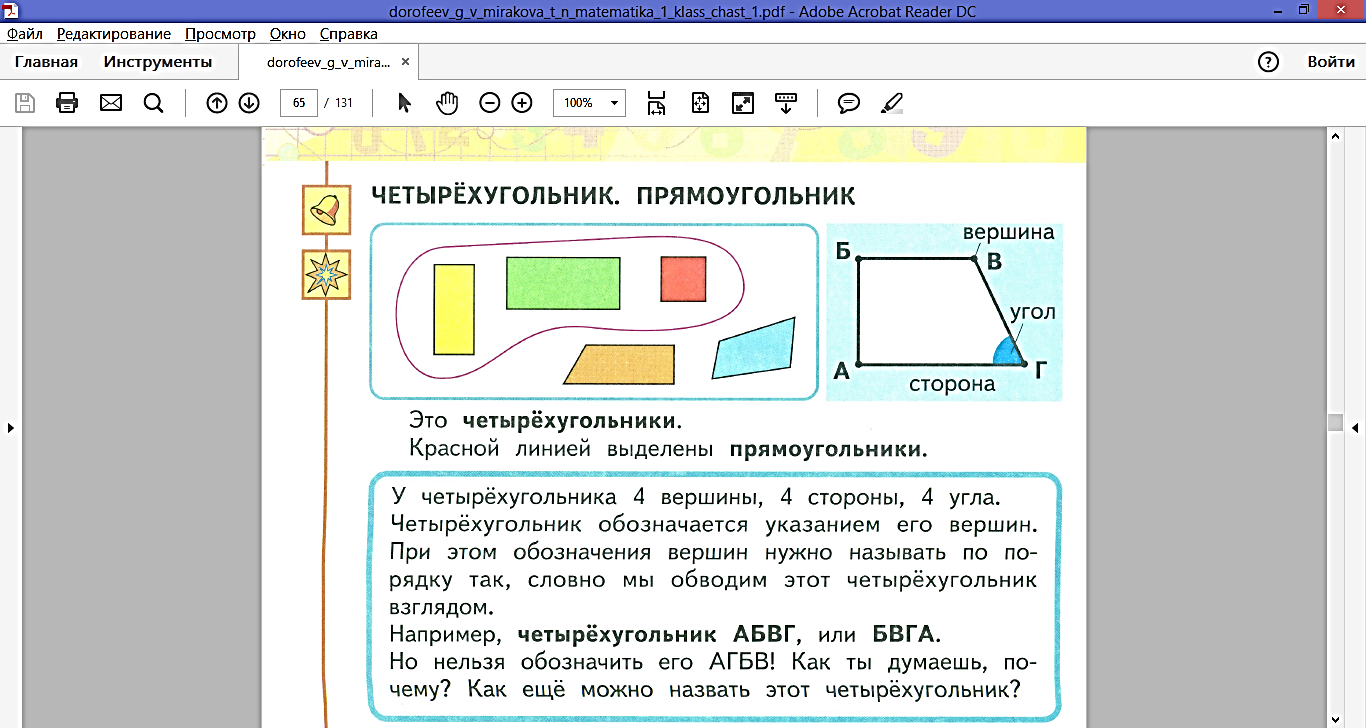
6. Какие виды определений используются, по Вашему мнению, при определении понятия «прямоугольник» в следующем случае (Моро, М.И., Бантова, М.А. и др. Математика. 2 класс: учебник. В 2 ч. Ч. 2., с. 14).
_____________________________________________________________
_____________________________________________________________
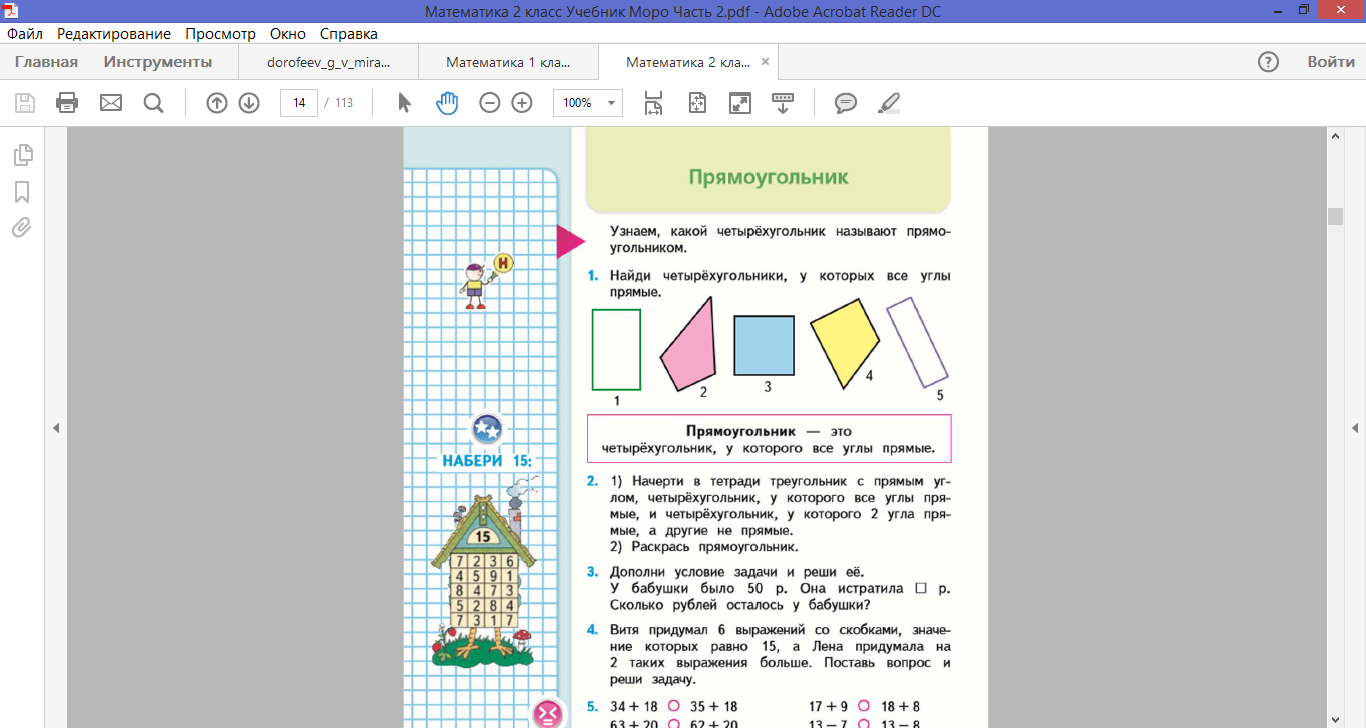
7. В учебниках математики для начальной школы понятие квадрата формулируется следующим образом: «Квадрат – это прямоугольник, у которого все стороны равны». Выделите в этом определении определяемое понятие, определяющее понятие, родовое понятие и видовое отличие. Какие еще понятия могут быть выбраны как родовые для понятия «квадрат»? Как при этом будет меняться видовое отличие?
Определяемое понятие:_________________________________________
Определяющее понятие:________________________________________
_____________________________________________________________
Родовое понятие:______________________________________________
Видовое отличие:______________________________________________
_____________________________________________________________
Другие варианты родовых понятий:_______________________________
_____________________________________________________________
_____________________________________________________________