Прогнозирование временных рядов

Цель работы

Изучение алгоритмов прогнозирования и оценка точности прогноза по ретроспективным данным показателей работы организации.

Теоретические сведения

Исследование динамики показателей работы организации, выявление и характеристика основных тенденций развития и моделей взаимосвязи дают основание для прогнозирования – определения ожидаемых показателей.

Важное место в прогнозировании занимают статистические методы прогноза. Применение прогнозирования предполагает, что закономерность развития, действующая в прошлом внутри ряда динамики, сохраниться и в прогнозируемом будущем. Теоретической основой распространения тенденции на будущее является свойство инерционности, которое позволяет выявить сложившиеся взаимосвязи между уровнями динамического ряда, а также между группой взаимосвязанных рядов динамики. Надежность прогноза возрастает для сопоставимых рядов динамики, полученных на основе использования единой методологии. Точность прогноза зависит от периода упреждения: чем короче период упреждения, тем более надежные и точные результаты дает прогнозирование. За короткий период не успевают сильно измениться условия работы организации и характер ее динамики.

Наиболее часто используются простейшие алгоритмы прогнозирования:

- по среднему абсолютному приросту при линейной тенденции развития показателя во времени;

- по среднему темпу роста, когда тенденция ряда характеризуется показательной кривой;

- аналитическим описанием линии тренда, когда на показатель оказывают влияние множество факторов, и ее рассматривают в виде временной функции;

- по корреляционным связям между показателями ряда на ограниченном по времени интервале наблюдения;

- по среднему уровню ряда динамики в случае стационарного характера изменения во времени анализируемого показателя и др.

Прогнозирование по среднему абсолютному приросту проводится по формуле: у_пр = у + Dу_*t, (1)

где у – последний уровень ряда динамики; t – период упреждения (прогноз); Dу – средний абсолютный прирост анализируемого показателя.

Прогнозирование по среднему темпу роста выполняется по формуле:

у_пр = у_*Т_р^t, (2)

где Т_р – средний темп роста показателя.

Простейшим является прогноз средним значением уровня ряда:

у_пр = у_ср, (3)

где у_ср – среднее значение уровня анализируемого ряда динамики.

При подборе кривых для описания тренда многочленами стоит задача выбора степени многочлена. Для определения степени многочлена вычисляется последовательность разностей временного ряда:

D_i⁽¹⁾=y(t_i) - y(t_i-1), i=2. 3, …n

………………………………… (4)

D_i^(k)= D_i^(k-1)- D_i-1^(k-1), i=k, k+1, k+2,…n.

Порядок разностей, при котором они становятся примерно одинаковыми, берется в качестве степени аппроксимирующего многочлена. Так, если малыми оказываются вторые разности D_i⁽²⁾, i=1, 2. 3, …n, то для прогнозирования тренда берется многочлен второй степени:

y(t)=a+bt+ct².

Прогнозирование стационарных случайных процессов по корреляционным связям между показателями ряда на ограниченном по времени интервале наблюдения выполняется по формуле:

у_пр = (у₀*(1 + у_1*у₄ + у_2*у₃ + у_3*у₂ + у_4*у₁ )) / (1 + у₄² + у₃² + у₂² + у₁² ), (5)

где у₀, у₁, у₂, у₃, у₄ – уровни динамического ряда с показателями работы организации, у₄ соответствует последнему значению уровня ряда.

Для оценки точности прогноза с помощью вычислительного эксперимента анализируемая выборка временного ряда разбивается на две части: начало временного ряда используется для обучения и выбора алгоритма прогнозирования, а конец выборки используется для оценки точности прогнозирования. Абсолютная погрешность прогнозирования вычисляется по формуле:

Dу_пр = у_пр – у, (6)

где Dу_пр – абсолютная погрешность прогнозирования, отклонение прогнозного уровня относительно истинного значения; у – истинный уровень ряда; у_пр – спрогнозированное значение уровня ряда.

Для анализа рядов динамики и их прогнозирования используются офисные информационные технологии, реализованные в электронной таблице EXCEL, а также ППП типа STATISTICA, Matlab, STATISTICA Neural Networks и др.

Пример. Имеются статистические данные за 24 месяца о негативном влиянии производства листового стекла на окружающую природную среду. Содержание концентрации оксида азота в дымовых газах отражено на рисунке 1.

Выполнить прогнозирование временного ряда с использованием аналитического описания линии тренда: экспонентой, моделью на нейронных сетях и с использованием нечетких множеств. Выбрать наиболее точный алгоритм прогнозирования по величине абсолютной погрешности прогноза на интервале прогнозирования в четыре месяца.

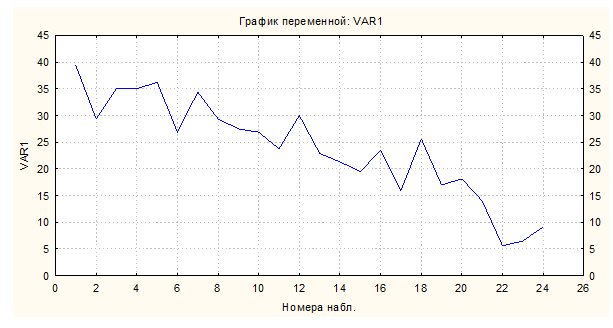Рисунок 1 - Содержание концентрации оксида азота в дымовых газах

Обучение алгоритма прогнозирования проводим по первым 20-и данным временного ряда, а точность прогнозирования оценим по последним четырем данным.

1) Визуальный анализ графика (рисунок 1) показывает возможность описания тренда многочленом. Оценим точность прогнозирования при аналитическом описании линии тренда простой экспонентой. Для этого воспользуемся ППП STATISTICA. Результаты математического описания линии тренда экспонентой и прогноза на четыре шага вперед отражены на рисунке 2. Параметры алгоритма - Эксп. сглажив.: S₀=39,37 T₀=-1,12 (прогноз выбросов) Лин. тренд, нет сезон.; Альфа= 0,100 Гамма=0,100 VAR1.

Вычислим погрешность прогнозирования по формуле (5) с 21 по 24 месяцы временного ряда (таблица 1).

Месяц
Фактическое значение		5,56	6,5	9,12
Расчетный прогноз	15,3	14,24	13,15	12,1
Погрешность прогноза	1,3	8,68	6,65	2,98

Таблица 1 – Погрешность прогнозирования

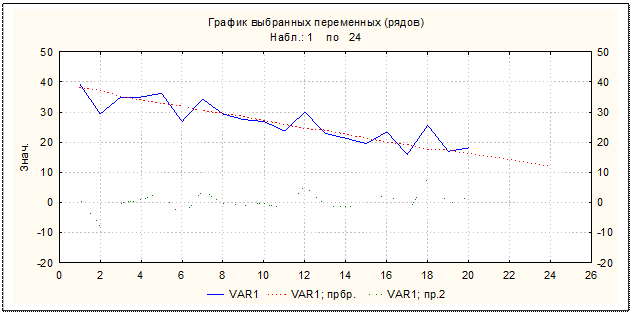Рисунок 2- Прогнозирование тренда

Наибольшая погрешность прогнозирования концентрации вредных веществ в выбросах линейным трендом равна Dу_пр =8,68 (мг/куб.дм).

2) Проведем анализ точности прогнозирования временного ряда с использованием моделей на нечетких множествах в ППП Matlab. Для этих целей составляем программу в виде М-файла (программа приведена ниже).

		% ПОСТРОЕНИЕ МОДЕЛИ МВМВ: fis = genfis2(vremj, rjd, 0.44); % ГДЕ: %- vremj, rjd - МАТРИЦЫ ВХОДНЫХ/ВЫХОДНЫХ ИСХОДНЫХ ДАННЫХ %- 0.44 - РАЗМЕР КЛАСТЕРА ДЛЯ genefis2 % ПРОСМОТР МОДЕЛИ В РЕДАКТОРЕ МВМВ: fuzzy(fis);
	% ВЫПОЛНИТЬ НА МОДЕЛИ МВМВ ПРОГНОЗ ДЛЯ НАБЛЮДЕНИЙ 21-22: chkfuzout = evalfis(progvremj, fis); % где progvremj-интервалы времени прогнозирования (21-24); % chkfuzout-прогнозное значение временного ряда; % РАСЧЕТ ПО МОДЕЛИ МВМВ ВРЕМЕННОГО РЯДА ПРИ ОБУЧЕНИИ (1-20): model= evalfis(vremj, fis); % ГДЕ: model- СМОДЕЛИРОВАННЫЙ РЯД НА ОБУЧАЮЩЕЙ ВЫБОРКЕ (1-20); % РАСЧЕТ ВРЕМЕННОГО РЯДА С ПРОГНОЗОМ (1-24): graf=unnamed1 + unnamed; % ГДЕ unnamed1- ФАЙЛ model ДОПИСАН ЧЕТЫРМЯ НУЛЯМИ В КОНЦЕ; % unnamed-ФАЙЛ С 20-ю НУЛЯМИ В НАЧАЛЕ ДОПИСАН В КОНЦЕ ФАЙЛОМ chkfuzout; % ПОСТРОЕНИЕ СОВМЕЩЕННОГО ГРАФИКА РАСЧЕТНОГО ВРЕМЕННОГО РЯДА % С ИСХОДНЫМ РЯДОМ (1-24): i=1; plot([graf(:,i), prognoz(:,i)]); legend('show');

Результаты моделирования временного ряда отображены на рисунке 3.

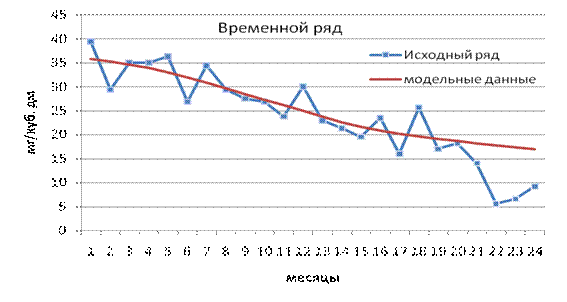
Рисунок 3 – Прогнозирование концентрации оксида азота в дымовых

газах моделью на нечетких множествах

Расчеты погрешности прогнозирования представлены в таблице 2. Наибольшая погрешность прогнозирования концентрации вредных веществ в выбросах моделью на нечетких множествах составила Dу_пр =12,19 (мг/куб.дм).

Таблица 2 – Погрешность прогнозирования нечеткими множествами

Месяц	Фактическое значение	Расчетный прогноз	Погрешность прогноза
		18,18	4,18
	5,56	17,75	12,19
	6,5	17,34	10,84
	9,12	16,92	7,8

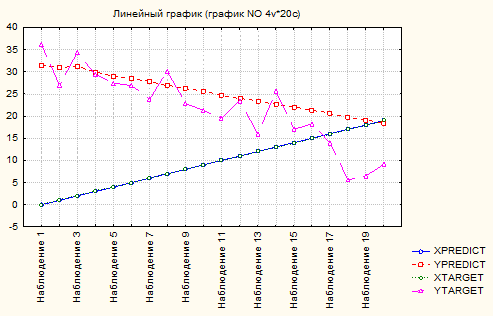
3) Опишем временной ряд нейронными сетями с использованием ППП STATISTICA Neural Networks. Для этих целей была выбрана сеть MLP с одним входом и 13 нейронами в промежуточном слое (рисунок 4).

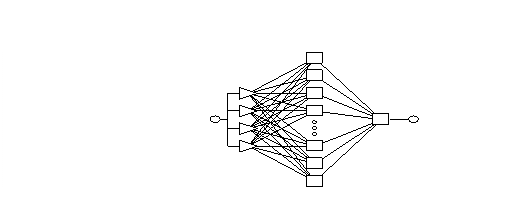
Рисунок 4 - Структура сети

Точность модели характеризуется следующими данными:

Регрессионная статистика

Tr. VAR1 Ve. VAR1 Te. VAR1

Data Mean 21.69637 23.95 19.45725

Data S.D. 11.19525 5.918922 7.485738

Error Mean 1.956998 -0.08533 5.082375

Error S.D. 6.769452 4.853207 7.110437

Abs E. Mean 5.758195 3.875791 5.375157

S.D. Ratio 0.6046718 0.8199477 0.9498645

Correlation 0.9013178 0.577145 0.3153473

Ошибка обучения равна 6,628, ошибка контроля 4,43 и ошибка тестирования 8,244. Результаты моделирования временного ряда приведены на рисунке 5.

Рисунок 5 - Прогнозирование концентрации оксида азота в дымовых

газах моделью на нейронных сетях

Проведенные исследования показали, что наибольшая точность прогнозирования достигается при аналитическом описании линии тренда простой экспонентой.

Задание к лабораторной работе

1) Выбрать тип кривой, соответствующей характеру изменения временного ряда.

2) Оценить точность прогнозирования временного ряда на интервале 3-5 шагов при описании тренда многочленом.

3) Оценить точность прогнозирования временного ряда с использованием модели на нечетких множествах.

4) Оценить точность прогнозирования временного ряда с использованием модели на нейронных сетях.

5) Выбрать наиболее точный алгоритм краткосрочного прогнозирования на интервале 3-5 шагов для исследуемого временного ряда.

6) Составить отчет по выполненным исследованиям.