Математическое описание дрейфующего объекта. Метод текущего регрессионного анализа
Цель работы
Целью лабораторной работы является ознакомление магистрантов с математическим описанием дрейфующих объектов. Магистранты приобретают навыки использования текущего регрессионного анализа при построении регрессионных моделей нестационарных объектов.
Теоретические сведения
При построении математического описания промышленных объектов приходится встречаться с фактом неконтролируемого изменения характеристик объекта во времени (дрейфом характеристик). Как правило, изменение дрейфующих параметров происходит значительно медленнее процесса изменения контролируемых переменных. Будем рассматривать случай, когда действительные значения коэффициентов изменяются во времени. Для этого выбирается адаптивный путь решения задачи.
При решении задачи построения математического описания дрейфующего объекта возможны ситуации двух типов:
1) по выборке наблюдений за входом и выходом объекта на некотором интервале времени от t0 до t>t0 необходимо найти оценки вектора коэффициентов модели, близкие к действительным значениям коэффициентов в момент t+α, где α≥0;
2) осуществляется непрерывное слежение за изменением коэффициентов модели. В любой момент времени t требуется найти наилучшее приближение к действительным значениям коэффициентов в момент t+α.
Будем рассматривать алгоритм вычисления оценок B(n+α), представленный в рекуррентной форме, связывающий оценку для момента (n+α) с ранее найденной оценкой для момента (n+α-1).
Значения оценок коэффициентов модели вычисляются для момента времени (n+α)
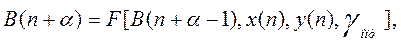
и в свою очередь
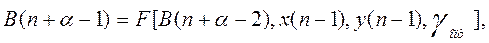 и т.д.
и т.д.
где F – функция, определяющая структуру алгоритма; γ – параметр алгоритма.
Оценки параметров модели будут состоятельными, когда переходной процесс заканчивается за конечное число шагов m. Длительность переходного процесса m зависит от выбора начального приближения B(α).
Запишем алгоритм вычисления параметров модели для метода текущего регрессионного анализа. Введем следующие обозначения:
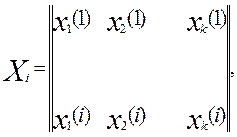 (1)
(1)
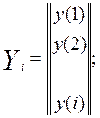 (2)
(2)
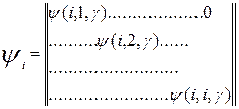 (3)
(3)
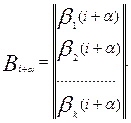 (4)
(4)
Параметры модели вычисляются по формуле:
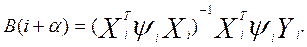 (5)
(5)
При 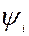 единичной матрицы выражение (5) совпадает с обычной мнк оценкой МРА.
единичной матрицы выражение (5) совпадает с обычной мнк оценкой МРА.
Допустим, что после определения оценки B(i+α) появляется дополнительная информация x(i+1), y(i+1) необходимо подсчитать B(i+α+1). Тогда можно вновь воспользоваться формулой (5) подставляя в нее изменив входящие в нее матрицы (1-3).
Пример. Построить модель для прогнозирования объема реализации продуктов фирмы. Объем реализации – это зависимая переменная Y (млн. руб.) В качестве независимых, объясняющих переменных выбраны: расходы на рекламу X 1 (тыс. руб.), цена товара X2 (руб.), средняя цена товара у конкурентов X3 (руб.), индекс потребительских расходов X4 (%). Дрейф параметров вызван влиянием времени на объем реализации продукции. Статистические данные по всем переменным приведены в табл.1.
Таблица 1- Данные объема реализации одного из продуктов фирмы
| Y | X1 | X2 | X3 | X4 |
| Объем реализации | Реклама | Цена | Цена конкурента | Индекс потребительских расходов |
| 4,8 | 14,8 | 17,3 | 98,4 | |
| 3,8 | 15,2 | 16,8 | 101,2 | |
| 8,7 | 15,5 | 16,2 | 103,5 | |
| 8,2 | 15,5 | 104,1 | ||
| 9,7 | ||||
| 14,7 | 18,1 | 20,2 | 107,4 | |
| 18,7 | 15,8 | 108,5 | ||
| 19,8 | 15,8 | 18,2 | 108,3 | |
| 10,6 | 16,9 | 16,8 | 109,2 | |
| 8,6 | 16,3 | 110,1 | ||
| 6,5 | 16,1 | 18,3 | 110,7 | |
| 12,6 | 15,4 | 16,4 | 110,3 | |
| 6,5 | 15,7 | 16,2 | 111,8 | |
| 5,8 | 17,7 | 112,3 | ||
| 5,7 | 15,1 | 16,2 | 112,9 |
Исходные данные представим в матричной формах Матрицу факторных переменных дополним фиктивной переменной Х0.
| X0 | х1 | х2 | х3 | х4 |
| 4,8 | 14,8 | 17,3 | 98,4 | |
| 3,8 | 15,2 | 16,8 | 101,2 | |
| 8,7 | 15,5 | 16,2 | 103,5 | |
| 8,2 | 15,5 | 104,1 | ||
| 9,7 | ||||
| 14,7 | 18,1 | 20,2 | 107,4 | |
| 18,7 | 15,8 | 108,5 | ||
| 19,8 | 15,8 | 18,2 | 108,3 | |
| 10,6 | 16,9 | 16,8 | 109,2 | |
| 8,6 | 16,3 | 110,1 | ||
| 6,5 | 16,1 | 18,3 | 110,7 | |
| 12,6 | 15,4 | 16,4 | 110,3 | |
| 6,5 | 15,7 | 16,2 | 111,8 | |
| 5,8 | 17,7 | 112,3 | ||
| 5,7 | 15,1 | 16,2 | 112,9 |
Xi =
Yi =
Построим график (рис.1) изменения зависимой переменной Y для выявления нестационарности характеристик объекта, либо наличия тренда в выходной переменной
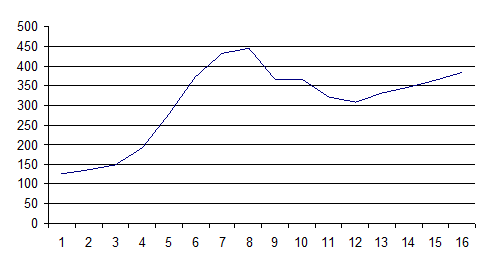
Рисунок 1 - Колебания объема реализации продукта фирмы
Из графика видна нестационарность объекта исследования. Этот факт обосновывает необходимость применения текущего регрессионного анализа для оценки параметров модели объекта.
Примем, что с «увеличением» возраста наблюдений ценность их для определения оценок B(i+α) убывает. Выбираем функцию веса следующего вид [1]:
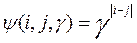 (6)
(6)
Параметр γ выбирается из интервале 0<γ<1.
Заполним матрицу функции «веса» принимая γ=0,9, i=8:
| 0,478 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | |
| 0,00 | 0,531 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | |
| 0,00 | 0,00 | 0,59 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | |
| ΨI = | 0,00 | 0,00 | 0,00 | 0,656 | 0,00 | 0,00 | 0,00 | 0,00 |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,729 | 0,00 | 0,00 | 0,00 | |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,81 | 0,00 | 0,00 | |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,9 | 0,00 | |
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 1,00 |
Вычислим параметры модели по формуле:
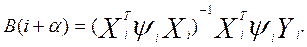
Результаты вычислений приведены ниже:
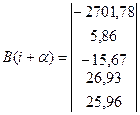
Рассчитаем по модели значения зависимой переменной для выборки i=8 и прогнозное значение для α=9, 10, ….16. Результаты вычислений наложим на график исходных данных (рис.2).
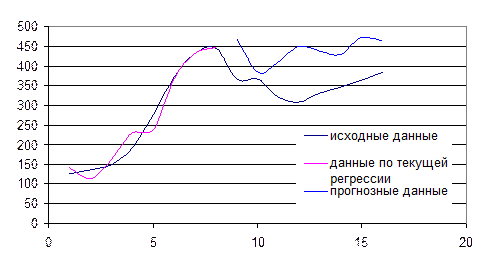
Рисунок 2 – Совмещенный график исходной выборки, расчетов по текущей регрессии и прогноза
Как следует из графика параметры модели, вычисленные по методу регрессионного анализа, хорошо описывают выборку i=8. Применение полученной модели для прогнозирования α=9, 10, ….16 не обеспечивает требуемую точность прогноза. Поэтому, необходимо вновь воспользоваться формулой (5) подставляя в нее изменив входящие в нее матрицы 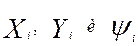 .
.
Задание к лабораторной работе
1) Записать исходные данные в матричной форме.
2) Построить график изменения зависимой переменной. Провести анализ стационарности объекта.
3) Выбрать функцию «веса» (6) с параметрами γ и i. Записать матрицу функции «веса».
4) Вычислить параметры модели.
5) Рассчитать по модели значения зависимой переменной для выборки размером i и прогноза. Расчетные значения наложить на график исходных данных.
6) Провести анализ совмещенных графиков с исходной выборкой, расчетами по текущей регрессии и прогноза.
