Методические указания к лабораторным занятиям
по дисциплине «Модели и методы планирования экспериментов, обработки экспериментальных данных» для магистрантов по направлениям:
09.04.02- Информационные системы и технологии, профиль
подготовки Информационные системы и технологии;
09.04.04 - Программная инженерия, профиль подготовки
Информационные системы и технологии
Учебное электронное издание
Владимир 2016
ББК 22.1я7
УДК 519.242 (076)
М15
Методические указания к лабораторным занятиям по дисциплине «Модели и методы планирования экспериментов, обработки экспериментальных данных» предназначены для подготовки магистров по дисциплинам по выбору по направлениям 09.04.02 «Информационные системы и технологии» и 09.04.04 «Программная инженерия» по профилю "Информационные системы и технологии».
Курс знакомит магистрантов с методами построения моделей, планированием экспериментов и обработкой экспериментальных данных. Обучаемые получают навыки постановки и проведения экспериментов по заданной методике, исследования экспериментальных данных процесса функционирования объектов и выбора оптимальных решений.
Лабораторная работа №1
Полный факторный эксперимент
Цель работы
Целью лабораторной работы является ознакомление магистрантов с использованием полного факторного эксперимента при исследовании объектов управления. Магистранты приобретают навыки постановки эксперимента, определения области планирования эксперимента, составления матриц планирования полного факторного эксперимента, расчетов коэффициентов регрессии, использования статистических критериев для оценки значимости коэффициентов и адекватности полученной математической модели.
Теоретические сведения
При планировании эксперимента важно учитывать следующее: стремление к минимизации числа опытов; одновременное варьирование всех переменных, определяющих процесс; выбор четкой стратегии, позволяющей принимать обоснованные решения после каждой серии экспериментов. В отличие от классического регрессионного анализа удается избежать корреляцию между коэффициентами уравнения регрессии.
При планировании по схеме полного факторного эксперимента (ПФЭ) реализуются все возможные комбинации факторов на двух выбранных для исследования уровнях. Количество опытов N при ПФЭ определяется по формуле: N = 2 k .
При полном факторном эксперименте уравнение регрессии принимает вид полинома первой степени:
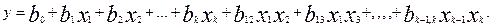
При выборе верхнего и нижнего уровней факторов необходимо учитывать ограничения, связанные со свойствами объекта исследования. На интервал варьирования так же накладываются ограничения: он не может быть меньше ошибки, с которой экспериментатор фиксирует уровень фактора, и не может быть настолько большим, что верхний и нижний уровень окажутся за пределами области определения.
Пример. Дана структура модели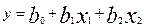 
.Проведен ПФЭ 22 с центром z10=50, z20=60 с шагом варьирования ∆z1=30, ∆z2=30. Каждая строка плана содержит по три параллельных опыта (m=3). Матрица плана приведена в табл.1.
Таблица 1- Полный факторный эксперимент 22
| Опыты | Факторные переменные | Зависимые переменные | ||||
| x0 | x1 | x2 | y1 | y2 | y3 | |
| -1 | -1 | 7,9 | 6,5 | 5,3 | ||
| +1 | -1 | 7,0 | 9,1 | 15,8 | ||
| -1 | +1 | -7,2 | -6,8 | -6,9 | ||
| +1 | +1 | 3,7 | 6,6 | 6,3 |
Рассчитаем дисперсии погрешностей в строках матрицы планирования по формуле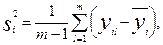 
где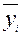 
среднее арифметическое значение зависимой переменной в i-й строке плана, i=1,2,3,4.
Расчетные значения дисперсии воспроизводимости опытов равны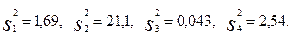 
Определим однородность дисперсий воспроизводимости в опытах ПФЭ по критерию Кохрена:
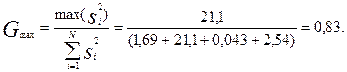
Критическое значение критерия Кохрена для уровня значимости α=0,01 и числа степеней свободы f1=(m-1)=2 и f2=N=4 равно 0,864. Так как расчетное значения критерия меньше критического значения, то дисперсии воспроизводимости опытов в строках матрицы планирования можно считать оценками одной и той же генеральной дисперсией воспроизводимости опытов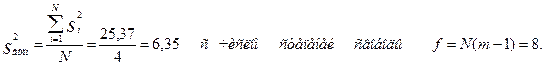 
Рассчитываем коэффициенты уравнения регрессии по формуле: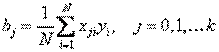 
получаем b0=3,94; b1=4,14; b2=-4,66.
Уравнение регрессии принимает вид:
y=3,94 + 4,14x1 – 4,66x2.
Оцениваем значимость коэффициентов регрессии по критерию Стьюдента, для чего определяем дисперсию погрешности коэффициентов регрессии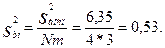 
Расчетные значения t-критерия определяются по формуле: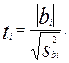 
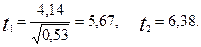Находим критическое значение критерия для уровня значимости α=0,05 и числа степеней свободы f=8: tкр=2,3. Так как расчетные значения t-критерия больше критического, то коэффициенты регрессии признаются значимыми.
Для проверки адекватности уравнения регрессии рассчитываем F-критерий: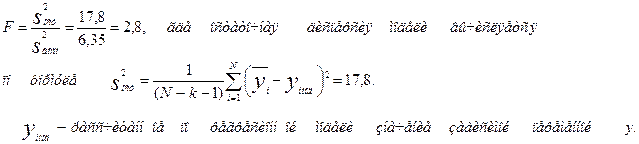 
Критическое значение критерия Фишера для уровня значимости α=0,05 и числа степеней свободы f1=1, f2=8 равно Fкр=5,32. Так как расчетное значения критерия F=2,8 меньше критического Fкр=5,32, то модель считается адекватной.
Задание к лабораторной работе
1) Построить матрицу планирования для получения линейной модели с учетом парных взаимодействий факторных переменных.
2) Рассчитать линейные и парные коэффициенты взаимодействий регрессионной модели.
3) Оценить значимость расчетных коэффициентов. Отбросить незначимые коэффициенты из структуры модели.
4) Оценить адекватность уравнения регрессии.
5) Оценить влияние факторов на зависимую переменную