Расчетно-практическая работа №5.

Тема: «Растяжение и сжатие»

Цель:

1) закрепитьосновные понятия сопротивления материалов деформация растяжения сжатия;

2) производить расчеты на сжатие;

3) производить расчеты элементов конструкций на прочность;

4) строить эпюры напряжений.

Время выполнения: 8 часов.

Для выполнения задания необходимо знать:

Растяжением или сжатием называется такой вид деформации, при кото­ром в поперечном сечении бруса возникает один ВСФ — продольная сила N. Она равна алгебраической сумме проекций на про­дольную ось внешних сил, действующих на отсеченную часть бруса:

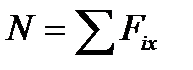(23)

Так как величина продольных сил в разных сечениях бруса неодинакова, то строится эпюра продольных сил. Эпюра продольных сил - график, показывающий изменения ве­личины продольных сил в сечении бруса по его длине.

Последовательность построения эпюр продольных сил:

1. Разбиваем брус на участки, ограниченные точками приложения сил (нумерацию участков ведем от незакрепленного конца).

2. Используя метод сечений, определяем величину продольных сил в се­чении каждого участка.

3. Выбираем масштаб и строим эпюру продольных сил, т.е. под изобра­жением бруса (или рядом) проводим прямую, параллельную его оси, и от этой прямой проводим перпендикулярные отрезки, соответствующие в выбран­ном масштабе продольным силам (положительное значение откладываем вверх (или вправо), отрицательное — вниз (или влево)).

Под действием продольных сил в поперечном сечении бруса возникает нормальное напряжение, которое определяется по формуле:

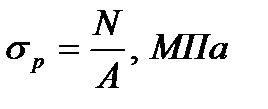(24)

где

А — площадь поперечного сечения участка.

Гипотеза плоских сечений устанавливает, что при растяжении (сжатии) сечение бруса остается плоским и перпендикулярным линии действия силы. Закон Гука при растяжении - нормальное напряжение, возникающее в поперечных сечениях при растяжении в пределах упругости, прямо пропорционально продольной деформации:

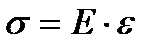(25)

где

Е — коэффициент пропорциональности, который называется модулем упругости.

Он характеризует жест­кость материала, из которого изготовлен элемент конструкции. Для различных материалов его значения определены экспериментально.

Закон Гука для определения деформации растяжения:

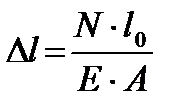(26)

где

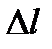— абсолютное изменение продольных размеров;

l₀ — первоначальные размеры элемента;

ЕА — величина, характеризующая жесткость сечения бруса.

Условие прочности при растяжении: рабочее напряжение должно быть меньше или равно допускаемому напряжению, т.е.

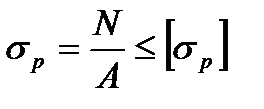(27)

Используя это условие, можно выполнить три вида расчетов на прочность при растяжении.

1) Проверочный — проверка прочности: по заданной рабочей нагрузке и заданному размеру сечения определяем рабочее напряжение и сравниваем его с допускаемым напряжением. Если 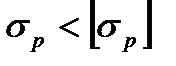- удовлетворяет условию проч­ности , если 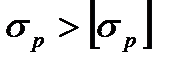- не удовлетворяет условию проч­ности

2) Проектный — подбор размера сечения по заданной рабочей нагрузке и допускаемому напряжению: (например для вала) -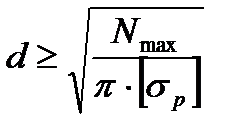

3) Проверочно-уточненный— определение допускаемого значения рабочей нагрузки по заданному размеру сечения и допускаемому напряжению. (например для круглого бруса):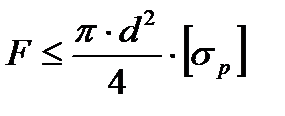

Задание(подставь и посчитай)

Определение деформации растяжения – сжатия ступенчатого бруса.

Построить эпюры продольных сил и нормальных напряжений для на­груженного стального винта(3) съёмника подшипников (рис. 25). Определить удлинение (укорочение) винта, если Е_ст= 2 ·10⁵ МПа.

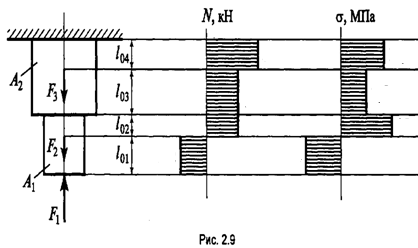
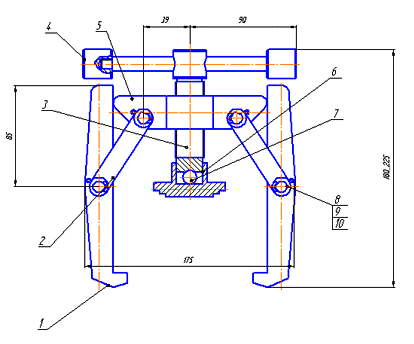
Рисунок 25

Дано: F₁ = кН; F₂ = кН ; F₃ = кН ;

А₁ = 2 см² = 2 ·10² мм² ; А₂ = 4 см² = 4 ·10² мм² ; Е_ст = 2 ·10⁵ МПа ; l₀₁ = 100 мм ; l₀₂ = 50 мм ; l₀₃ = 200 мм ; l₀₄ = 150 мм

Определить: ∆l

Решение.

1) Определяем продольные силы и строим их эпюру:

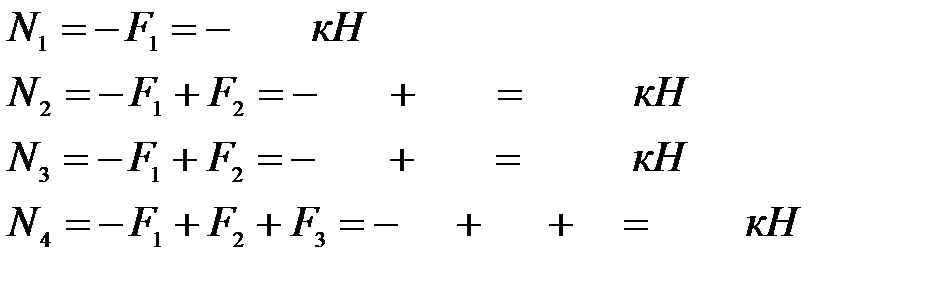
2) Определяем величину нормальных напряжений и строим их эпюру:

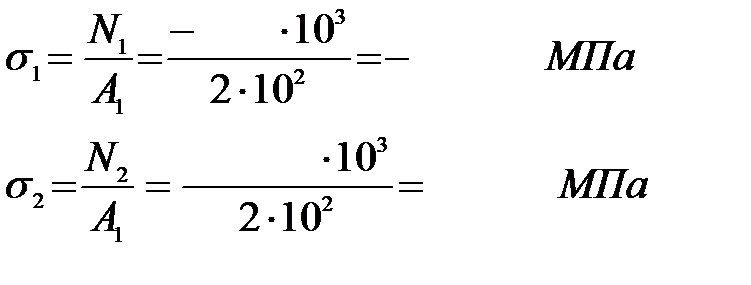
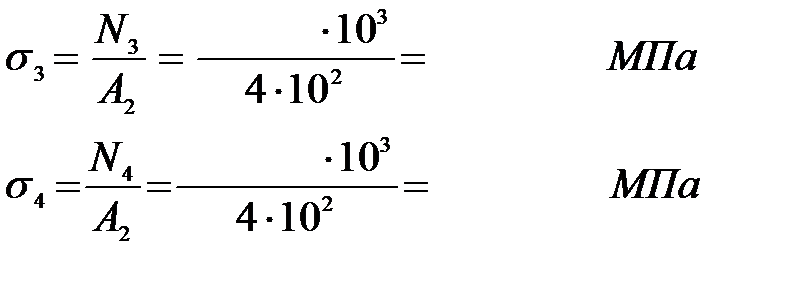
3) Используя видоизмененный закон Гука, определяем удлинение бруса:

∆l = ∆l₁ + ∆l₂ + ∆l₃ + ∆l₄ = мм.

Положительный знак ∆l говорит о том что брус растягивается, отрицательный, что сжимается.

Ответ: ∆l = мм.

Выполните решение задания, взяв данные в таблице 6.

Таблица 6.

№ варианта	Сила F1 , кН	Сила F2 , кН	Сила F3 , кН	№ варианта	Сила F1 , кН	Сила F2 , кН	Сила F3 , кН