Решение задач оптимизации в приложениях Mathcad и Excel

В приложении Mathcad имеются встроенные функции, с помощью которых можно решать задачи оптимизации. Рассмотрим пример.

Пусть требуется определить оптимальные значения x₁иx₂, которые обеспечивали бы максимум целевой функции

y = 1.7 + 4.56x₁ – 3x₂ – 0.69x₁x₂ – 0.44x₂²

и удовлетворяли ограничениям:

3 <= x₁ <= 4, 0,1 <=x₂ <=0,9.

В рабочей области приложения Mathcad требуется записать:

f(x1, x2) := 1.7 + 4.56x1 – 3x2 – 0.69x1x2 – 0.44x2²

x1 := 3 x2 :=0.1

Given

4 ≥ x1 ≥ 3

0.9 ≥ x2 ≥ 0.1

R := maximize(f, x1, x2) R =

Встроенная функция minimize позволяет решить задачи оптимизации, в которых нужно определить минимум целевой функции.

В приложении Excel имеется специальная команда, с помощью которой можно решать задачи оптимизации. Например, чтобы решить предыдущий пример, можно произвести следующие действия.

– на рабочем листе, например в ячейке А1 записать значение левой границы для первого ограничения (число 3);

– в ячейке В1 записать значение левой границы для второго ограничения (число 0,);

– в ячейке С1 записать целевую функцию:

=1,7 + 4,56 ∙ А1 – 3 ∙ В1 – 0,69 ∙ А1 ∙ В1 – 0,44 ∙ В1^2

– выполнить Сервис/Поиск решения. В появившемся окне задать имя ячейки с целевой функцией (для данного примера С1), определить, что в задаче целевая функция стремится к максимуму, ввести соответствующие ограничения для содержимого ячеек А1 и В1.

Решение задачи можно посмотреть и проанализировать на отдельном листе.

Если в пункте меню Сервис команда Поиск решения отсутствует, то ее можно добавить, используя Сервис/Настройка.

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Решение уравнений первого порядка

Рассмотрим дифференциальное уравнение первого порядка:

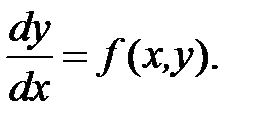
Требуется найти решение на интервале [x₀,x_n], удовлетворяющее начальному условию y(x₀) = y₀.

Для приближённого решения дифференциального уравнения интервал [x₀,x_n]разбивается на n частей с шагом h:

x_i+1 = x_i + h, i = 0, 1, 2, …, n – 1.

В полученных точках вычисляются значения y_i.

Метод Эйлера. Согласно методу Эйлера, значения y_i определяются по формуле:

y_i+1 = y_i + h × f(x_i, y_i).

Алгоритм метода Эйлера:

1. Ввод n, конечного значения x_n, начального значения x₀ (в переменную x),ввод y₀(в переменную y).

2. Вычисление h = 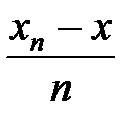, x = x₀, y = y₀.

3. Вывод x, y.

4. Вычисление y = y + h × f(x, y), x = x + h.

5. Если x > x_n, то переход к п. 6, иначе – переход к п. 3.

6. Конец вычислений.

Для получения достоверных результатов значение h должно быть достаточно мало, при этом можно не выводить все получающиеся значения xиy. Целесообразно внести изменения в алгоритм программы так, чтобы вычисления проводились с малым шагом, а вывод результатов − с большим.

Метод Рунге-Кутта. Расчетные формулы метода Рунге-Кутта четвертого порядка имеют вид:

k1 = h × f(x_i, y_i),

k2 = h × f(x_i + 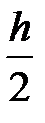, y_i + ),

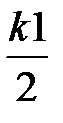k3 = h × f(x_i + 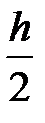, y_i + ),

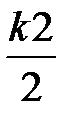k4 = h × f(x_i + h, y_i + k3),

y_i+1 = y_i + 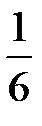× (k1 + 2 × k2 + 2 × k3 + k4),

x_i+1 = x_i + h, i = 0, 1, 2, …, n – 1.

Для разработки программы, реализующей метод Рунге-Кутта можно использовать тот же алгоритм, что и для метода Эйлера, внеся в него соответствующие изменения.