Лабораторная работа № 1 Системы счисления

Правило перевода чисел произвольного основания в десятичную систему счисления

Для перевода целого числа в десятичную систему счисления достаточно представить число согласно выражению и вычислить полученное выражение (1). Например.

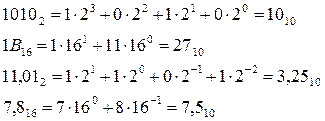
Правило перевода чисел из десятичной системы счисления в систему счисления c произвольным основанием

Целое число

Целое число делится нацело на основание системы счисления, затем на это основание делятся все частные от целочисленного деления, до тех пор пока частное не станет меньше основания. В результат заносится последнее частное и все остатки от деления, начиная с последнего.

Пример. Переведем число 23 в двоичную, восьмеричную и шестнадцатеричную системы счисления.

1) 23 2 11 2 5 2 2 2

22 11 10 5 4 2 2 1

1 1 1 0

Следовательно

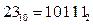
2) 23 8 Следовательно,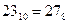

16 2

7

3) 23 16 Следовательно,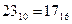

16 1

Для перевода правильной дроби из одной системы счисления в другую необходимо выполнить следующие действия:

a) отделить вертикальной чертой дробную часть от целой;

b) умножить дробную часть на основание новой системы счисления, записав результат строго под исходным числом, начиная с младшего разряда; в случае, если получится перенос в целую часть числа, записать его слева от вертикальной черты;

c) дробную часть полученного числа снова умножить на основание новой системы счисления и т.д.; умножение выполнять до тех пор, пока либо будет полученное число с заданной точностью, либо справа от вертикальной черты окажется нуль.

Результатом перевода будет число, полученное слева от вертикальной черты, при чтении сверху вниз. При выполнении перевода необходимо умножение производить в исходной системе счисления и основание новой системы счисления тоже представить в исходной системе.

Примеры:1) Перевести число 0,728 в восьмеричную систему:

× 8

0 728

5 824 Следовательно,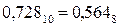

6 592

4 736

2) Перевести число 0,752₈ в десятичную систему счисления

× 12 , где 10₁₀=12₈

0 752

9 ↔ 11 444 Следовательно,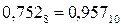

5 550

7 020

Для перевода неправильной дроби следует отдельно перевести целую часть, отдельно дробную часть.

Пример. Осуществить перевод числа 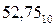в двоичную систему счисления.

1. выполним перевод целой части

52| 2 26| 2 13| 2 6| 2 3 | 2

4 26 26 13 12 6 6 3 2 1

12 0 1 0 1

12

Следовательно, 52₁₀→110100₂

2. выполним перевод дробной части

×2

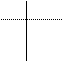0 75 Следовательно, 0,75₁₀→0,11₂

1 5

1 0

Общий вывод: 52,75₁₀→110100,11₂ .

Арифметические действия в различных системах счисления

Двоичная система счисления

Арифметические операции в двоичной системе счисления выполняются по правилам, указанным в таблице 2.

Таблица 2 – Арифметические операции в двоичной системе счисления

сложение	вычитание	умножение
0+0=0	0 - 0=0	0*0=0
0+1=1	1 - 0=1	0*1=0
1+0=1	1 - 1=0	1*0=0
1+1=10	10 – 1=1	1*1=1

Примеры:

1) 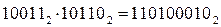2)

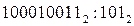
10011 100010011 101

^× 10110 101 110111

00000 111

10011 101

10011 1000

00000 0000

10011 101

110100010 111

101

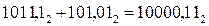3) 4)

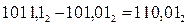
1011,1 1011,1

+ 101,01 - 101,01

0000,11 110,01

Варианты индивидуальных заданий к лабораторной работе №1

Задания:

1.Выполните перевод чисел из указанной системы счисления в десятичную систему счисления.

2.Выполните перевод числа из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.

3.Выполните сложение чисел в указанной системе счисления.

4.Выполните вычитание в указанной системе счисления.

5.Выполните умножение в указанной системе счисления.

1 вариант

1) а) 10011,101₂; б) 47,12₈; в) 4С,2₁₆

2) 216,35

3) а) 236,47₈ + 524,55₈; б) 42,А3₁₆+142,93₁₆

4) 412,39₁₆ – 87,А₁₆; б) 1011010,01₂-101101,1₂ в) 214,12₈-67,35₈

5) а)25,6₈ ×5,6₈; б) 2,3₁₆ ×5,8₁₆

2 вариант

1) а) 1011,01₂; б) 62,23₈; в) 18,2₁₆

2) 541,3

3) а) 362,45₈ + 72,7₈; б) 263,43₁₆+С2,98₁₆

4) а)5С3,21₁₆ –157,8₁₆; б) 11011011,101₂-1101011,11₂ в) 362,21₈-76,56₈

5) а)34,5₈ ×2,4₈; б) А2,2₁₆ ×5,6₁₆

3 вариант

1) а) 1101101,1₂; б) 52,3₈; в) 29,5₁₆

2) 63,8

3) а)852,А2₁₆ + 142,1₁₆; б) 263,43₈+57,66₈

4) а)412,3₈ – 67,5₈; б)10100011,01₂-1101011,11₂ в) 1B3,24₁₆-76,56₁₆

5) а)3,14₈ ×7,5₈; б)B2,2₁₆ ×6,7₁₆

4 вариант

1) а) 101010,001₂; б) 57,24₈; в) 5F,А4₁₆

2) 421,3

3) а)D42,3₁₆ + 57,63₁₆; б) 534,36₈+76,34₈

4) а)75,36₈ – 35,7₈; б) 101010,1001₂-1011,1111₂ в) 43A,42₁₆-98,67₁₆

5) а)54,21₈ ×2,5₈; б) 453,5₁₆ ×8,7₁₆

5 вариант

1) а) 110011,101₂; б) 24,32₈; в) 2D,34₁₆

2) 461,24

3) а)289,01₁₆ + 25,37₁₆; б) 546,76₈+157,64₈

4) а)423,11₈ – 134,65₈; б)1001110,001₂-110111,11₂ в) 253,34₁₆-3D,97₁₆

5) а)65,3₈ ×4,5₈; б) 36,54₁₆ ×3,4₁₆

6 вариант

1) а) 101110,01₂; б) 55,43₈; в) 98,3₁₆

2) 851,14

3) а)456,32₈ + 45,55₈; б) 756,D4₁₆ + 524,68₁₆

4) а)127,С2₁₆ – 79,9₁₆; б) 110110100,01₂-110111,11₂ в) 361,44₈-167,76₈

5) а)45,33₈ ×2,3₈; б) 36,54₁₆ ×5,8₁₆

7 вариант

1) а) 101110,1₂; б) 75,3₈; в) 56,68₁₆

2) 876,45

3) а)523,22₈ + 42,67₈; б)3E8,4₁₆+58,99₁₆

4) а)21В₁₆ – 78,1А₁₆; б)1010010,101₂-111101,11₂ в) 653,42₈-77,65₈

5) а)5,6₈ ×23,2₈; б) 36,5А₁₆ ×3,8₁₆

8 вариант

1) а) 10101,1101₂; б) 26,33₈; в) 14,3₁₆

2) 568,32

3) а)457,35₈ + 57,6₈; б) 563,F5₁₆+58,453₁₆

4) а)5F1,2₁₆ – 73,5₁₆; б)101000100,001₂-1101101,101₂ в) 332,55₈-76,65₈

5) а)5,3₈ ×5,5₈; б) 43, А3₁₆ ×25,6₁₆

9 вариант

1) а) 100011,01₂; б) 74,21₈; в) С4,2₁₆

2) 612,53

3) а)632,47₈ + 452,55₈; б) 6D7,94₁₆+247,4А3₁₆

4) а)214,39₁₆ – 78,А₁₆; б)101010,001₂-11101,101₂ в) 327,565₈-67,57₈

5) а)52,6₈ ×3,2₈; б)В5,45₁₆ ×5,6₁₆

10 вариант

1) а) 101100,001₂; б) 52,63₈; в) 85,3₁₆

2) 85,36

3) а)253,24₈ + 756,66₈; б) 558,E4₁₆+473,493₁₆

4) а)254,A1₁₆ – 123,53₁₆; б)11101010,011₂-1100101,101₂ в) 546,65₈-73,53₈

5) а)45,3₈ ×2,7₈; б) 8,45₁₆ ×6,6₁₆

11 вариант

1) а) 10100,11₂; б) 751,3₈; в) 1E,4₁₆

2) 854,32

3) а)24,А2₁₆ + 131,51₁₆; б) 577,67₈+364,43₈

4) а)354,2₈ – 54,65₈; б)101010010,01₂-1001001,101₂ в) 536,57₁₆-2C,59₁₆

5) а)2,54₈ ×7,5₈; б) 2,С₁₆ ×53,4₁₆

12 вариант

1) а) 111100,11₂; б) 55,61₈; в) 2E,35₁₆

2) 951,64

3) а)452,E2₁₆ + 231,14₁₆; б) 567,627₈+563,63₈

4) а)422,13₈ – 75,6₈; б)101010110,01₂-1011011,101₂ в) 237,57₁₆-87,5С9₁₆

5) а)5,7₈ ×5,6₈; б) 8,7₁₆ ×3,4₁₆

13 вариант

1) а) 110010,101₂; б) 451,32₈; в) 421,35₁₆

2) 592,34

3) а)249,59₁₆ + 1E,12₁₆; б) 347,237₈+443,73₈

4) а)653,25₈ – 76,6₈; б) 11010101,1011₂-1101001,101₂ в) 234,37₁₆-127,5А9₁₆

5) а)27,6₈ ×2,3₈; б) 3,7₁₆ ×5,4₁₆

14 вариант

1) а) 10101,101₂; б) 535,6₈; в) 1С4,2₁₆

2) 582,31

3) а)456,35₈ + 452,73₈; б) 564,237₁₆+654,73₁₆

4) а)4F2,31₁₆ – 78,9₁₆; б) 101011101,1011₂-11010111,101₂ в) 434,47₈-226,56₈

5) а)42,36₈ ×3,2₈; б) 6,7₁₆ ×14,4₁₆

15 вариант

1) а) 10110,001₂; б) 462,36₈; в) 451,32₁₆

2) 568,64

3) а)256,46₈ + 756,66₈; б) 554,277₁₆+454,73₁₆

4) а)163,45₁₆ – 2C,67₁₆; б)101010001,101₂-11010111,011₂ в) 634,27₈-276,56₈

5) а)54,63₈ ×4,5₈; б) А,7₁₆ ×4,5₁₆

16 вариант

1) а) 101110,01₂; б) 55,43₈; в) 98,3₁₆

2) 851,14

3) а)456,32₈ + 45,55₈; б) 756,D4₁₆ + 524,68₁₆

4) а)127,С2₁₆ – 79,9₁₆; б) 110110100,01₂-110111,11₂ в) 361,44₈-167,76₈

5) а)45,33₈ ×2,3₈; б) 36,54₁₆ ×5,8₁₆

17 вариант

1) а) 101110,1₂; б) 75,3₈; в) 56,68₁₆

2) 876,45

3) а)523,22₈ + 42,67₈; б)3E8,4₁₆+58,99₁₆

4) а)21В₁₆ – 78,1А₁₆; б)1010010,101₂-111101,11₂ в) 653,42₈-77,65₈

5) а)5,6₈ ×23,2₈; б) 36,5А₁₆ ×3,8₁₆

18 вариант

1) а) 10101,1101₂; б) 26,33₈; в) 14,3₁₆

2) 568,32

3) а)457,35₈ + 57,6₈; б) 563,F5₁₆+58,453₁₆

4) а)5F1,2₁₆ – 73,5₁₆; б)101000100,001₂-1101101,101₂ в) 332,55₈-76,65₈

5) а)5,3₈ ×5,5₈; б) 43, А3₁₆ ×25,6₁₆

19 вариант

1) а) 100011,01₂; б) 74,21₈; в) С4,2₁₆

2) 612,53

3) а)632,47₈ + 452,55₈; б) 6D7,94₁₆+247,4А3₁₆

4) а)214,39₁₆ – 78,А₁₆; б)101010,001₂-11101,101₂ в) 327,565₈-67,57₈

5) а)52,6₈ ×3,2₈; б)В5,45₁₆ ×5,6₁₆

20 вариант

1) а) 101100,001₂; б) 52,63₈; в) 85,3₁₆

2) 85,36

3) а)253,24₈ + 756,66₈; б) 558,E4₁₆+473,493₁₆

4) а)254,A1₁₆ – 123,53₁₆; б)11101010,011₂-1100101,101₂ в) 546,65₈-73,53₈

5) а)45,3₈ ×2,7₈; б) 8,45₁₆ ×6,6₁₆

21 вариант

1) а) 10100,11₂; б) 751,3₈; в) 1E,4₁₆

2) 854,32

3) а)24,А2₁₆ + 131,51₁₆; б) 577,67₈+364,43₈

4) а)354,2₈ – 54,65₈; б)101010010,01₂-1001001,101₂ в) 536,57₁₆-2C,59₁₆

5) а)2,54₈ ×7,5₈; б) 2,С₁₆ ×53,4₁₆

22 вариант

1) а) 111100,11₂; б) 55,61₈; в) 2E,35₁₆

2) 951,64

3) а)452,E2₁₆ + 231,14₁₆; б) 567,627₈+563,63₈

4) а)422,13₈ – 75,6₈; б)101010110,01₂-1011011,101₂ в) 237,57₁₆-87,5С9₁₆

5) а)5,7₈ ×5,6₈; б) 8,7₁₆ ×3,4₁₆

23 вариант

1) а) 110010,101₂; б) 451,32₈; в) 421,35₁₆

2) 592,34

3) а)249,59₁₆ + 1E,12₁₆; б) 347,237₈+443,73₈

4) а)653,25₈ – 76,6₈; б) 11010101,1011₂-1101001,101₂ в) 234,37₁₆-127,5А9₁₆

5) а)27,6₈ ×2,3₈; б) 3,7₁₆ ×5,4₁₆

24 вариант

1) а) 10101,101₂; б) 535,6₈; в) 1С4,2₁₆

2) 582,31

3) а)456,35₈ + 452,73₈; б) 564,237₁₆+654,73₁₆

4) а)4F2,31₁₆ – 78,9₁₆; б) 101011101,1011₂-11010111,101₂ в) 434,47₈-226,56₈

5) а)42,36₈ ×3,2₈; б) 6,7₁₆ ×14,4₁₆

25 вариант

1) а) 10110,001₂; б) 462,36₈; в) 451,32₁₆

2) 568,64

3) а)256,46₈ + 756,66₈; б) 554,277₁₆+454,73₁₆

4) а)163,45₁₆ – 2C,67₁₆; б)101010001,101₂-11010111,011₂ в) 634,27₈-276,56₈

5) а)54,63₈ ×4,5₈; б) А,7₁₆ ×4,5₁₆

26 вариант

1) а) 1101000,101₂; б) 72,73₈; в) 69,8₁₆

2) 95,32

3) а)251,74₈ + 776,66₈; б) 658,E4₁₆+873,493₁₆

4) а)354,A1₁₆ – 223,53₁₆; б)10101010,011₂-1110101,101₂ в) 576,65₈-75,53₈

5) а)46,3₈ ×3,7₈; б) 9,45₁₆ ×7,6₁₆

27 вариант

1) а) 10101,1101₂; б) 26,33₈; в) 14,3₁₆

2) 568,32

3) а)457,35₈ + 57,6₈; б) 563,F5₁₆+58,453₁₆

4) а)5F1,2₁₆ – 73,5₁₆; б)101000100,001₂-1101101,101₂ в) 332,55₈-76,65₈

5) а)5,3₈ ×5,5₈; б) 43, А3₁₆ ×25,6₁₆

28 вариант

1) а) 100011,01₂; б) 74,21₈; в) С4,2₁₆

2) 612,53

3) а)632,47₈ + 452,55₈; б) 6D7,94₁₆+247,4А3₁₆

4) а)214,39₁₆ – 78,А₁₆; б)101010,001₂-11101,101₂ в) 327,565₈-67,57₈

5) а)52,6₈ ×3,2₈; б)В5,45₁₆ ×5,6₁₆

29 вариант

1) а) 101101,101₂; б) 567,36₈; в) 951,32₁₆

2) 768,64

3) а)356,46₈ + 556,66₈; б) 454,277₁₆+554,73₁₆

4) а)263,45₁₆ – 3C,67₁₆; б)101010111,101₂-11010101,011₂ в) 734,27₈-376,56₈

5) а)74,63₈ ×4,5₈; б) А,3₁₆ ×6,5₁₆

Вопросы для самоконтроля

1. Что такое система счисления?

2. Что такое позиционная система счисления? Приведите примеры.

3. Что такое непозиционная система счисления? Приведите примеры.

4. Сформулируйте правило перевода чисел любой системы счисления в десятичную систему счисления.

5. Сформулируйте правило перевода целого числа десятичной системы счисления в любую систему счисления.

6. Сформулируйте правило перевода дробного числа десятичной системы счисления в любую систему счисления.

7. Сформулируйте правило перевода двоичного числа в восьмеричное.

8. Сформулируйте правило перевода шестнадцатеричного числа в двоичное.

9. Перечислите цифры восьмеричной системы счисления.

10. Перечислите цифры шестнадцатеричной системы счисления.

Лабораторная работа № 1 Системы счисления

Цель:Получение сведений о различных системах счисления и их применении для ЭВМ. Получение практических навыков по переведу чисел из одной системы счисления в другую и выполнению арифметических операций в различных системах счисления.

1 Теоретическая справка

Для регистрации сигналов используются различные средства их формализации – изображения, символы и т.д. Для отображения количественных характеристик описываемых объектов и последующей обработки этой информации уже в древности были изобретены специальные знаки (цифры) и приемы их комбинирования.

Совокупность приемов наименования и записи чисел с помощью цифр называют системой счисления. В любой такой системе имеется ряд символов называемых базисными цифрами; все остальные числа отображаются с помощью базисных цифр посредством определенных математических операций.

Системы счисления различаются как выбором базисных цифр, так и правилами образования из них произвольных чисел. Все их можно разделить на два больших класса – непозиционные и позиционные.

В непозиционных системах значение цифры не зависит от места, занимаемого ею в записи числа. Примером может служить римская система счисления.

В позиционных системах счисления значение любой базисной цифры зависит от ее места в записи числа; это место называется позицией, а количество используемых базовых - основанием системы счисления.

Основание системы счисления, в которой записано число, обычно обозначается нижним индексом. Например, 555_{7 –} число, записанное в семеричной системе счисления. Если число записано в десятичной системе, основание, как правило, не указывается.

Рассмотрим последовательность цифр, изображающую некоторое число, в котором целая и дробная части разделены запятой:

.

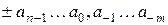Если считать, что приведенная выше последовательность изображает число в системе счисления с основанием k, то каждая из цифр этой последовательности может принимать одно из значений диапазона .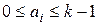

Для оценки количественного значения каждого разряда числа используется основание системы счисления, которое указывает, во сколько раз единица i+1 разряда больше единицы i младшего разряда. Учитывая сказанное, заданное число можно представить так:

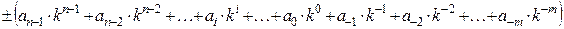(1)

Данное выражение используется для записи чисел в любой позиционной системе счисления.

где 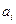- цифры в представлении данного числа. Так например,

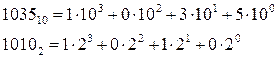
Наибольший интерес при работе на ЭВМ представляют системы счисления с основаниями 2, 8 и 16. Особенно удобна для ЭВМ двоичная система, так имеет несомненные технические и математические преимущества;

при ее аппаратной реализации можно использовать физические элементы с двумя возможными состояниями (есть ток – нет тока, намагничен – не намагничен и т.д.);

представление информации посредством только двух состояний особенно надежно и помехоустойчиво;

возможно применение стандартного аппарата булевой алгебры для выполнения логических преобразований.

Рассмотрим таблицу чисел в различных системах счисления:

Таблица 1 – Числа в различных системах счисления

Десятичная система счисления	Двоичная система счисления	Восьмеричная система счисления	Шестнадцатеричная система счисления
			A
			B
			C
			D
			E
			F