Арифметические действия в различных системах счисления
Для чисел, записанных в десятичной системе, мы пользуемся правилами сложения и умножения чисел «столбиком», деления — «углом». Эти же правила полностью применимы и для чисел, записанных в любой другой позиционной системе.
Рассмотрим сложение чисел. Как в десятичной, так и в любой другой системе мы складываем сначала единицы, затем переходим к следующему разряду и т. д. до тех пор, пока не дойдем до самого старшего из имеющихся разрядов. При этом необходимо помнить, что всякий раз, когда при сложении в предыдущем разряде получается сумма, большая чем основание той системы счисления, в которой ведется запись, или равная ему, надо сделать перенос в следующий (старший) разряд. Рассмотрим примеры.
1. Сложить два числа в восьмеричной системе счисления: 1234567(8)+1234567(8).
Как уже было отмечено ранее, операция сложения двух чисел начинается с цифр самого младшего разряда. Процесс сложения можно проследить по схеме.
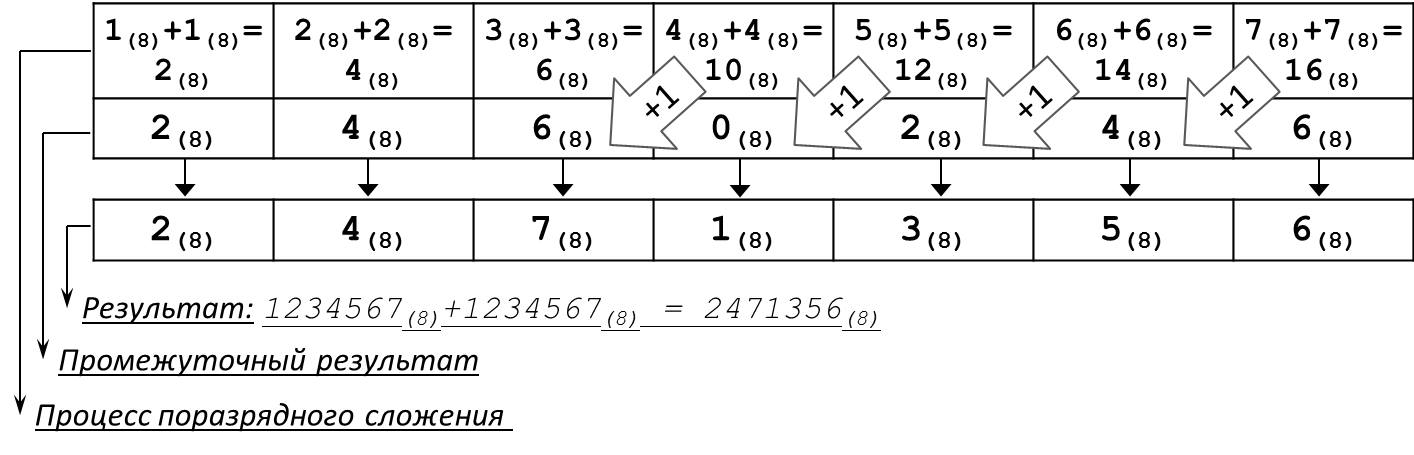
Рисунок
2. Сложить два числа в шестеричной системе счисления: 12345(6)+12345(6).
Схема сложения:
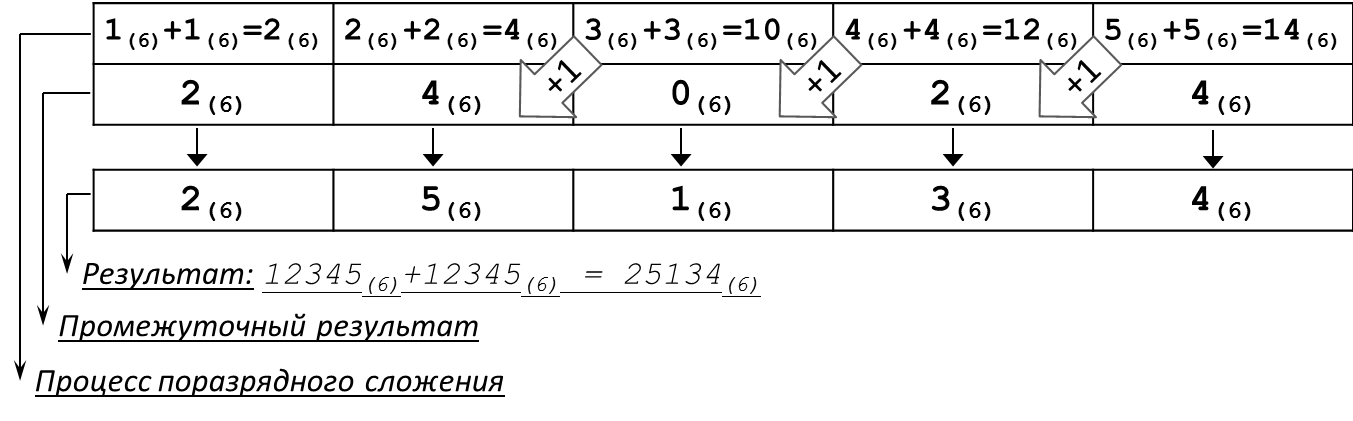
Рисунок
Для ускорения выполнения операций сложения можно пользоваться таблицами для различных систем счисления (см. Приложение ).
Перейдем теперь к умножению. Для определенности выберем какую-нибудь конкретную систему, скажем шестеричную. Основой для перемножения любых чисел служит таблица умножения, определяющая произведения чисел, меньших, чем основание системы счисления.
Рассмотрим умножение двух чисел столбиком. Из школьного курса мы знаем, что умножение столбиком производится в два этапа:
1) первый множитель последовательно умножается на все цифры второго множителя, начиная с цифры младшего разряда. При этом каждый последующий результат записывается в столбик со сдвигом влево на один разряд;
2) выполняется операция сложения столбиком всех полученных промежуточных результатов.
Замечание. Все операции, как сложение, так и умножение производятся в определенной системе счисления.
Рассмотрим описанную процедуру на примере. Умножить два числа в четверичной системе счисления: 123(4)*123(4).
Все вычисления производятся в четверичной систем счисления. Для удобства и большей наглядности вычислений составим таблицу соответствия чисел в десятичной и четверичной систем счисления (табл. ), а также таблицы операций сложения и умножения для четверичной системы счисления (табл ).
| Сложение | Умножение | |||||||
| A(10) | A(4) | A(10) | A(4) | A(10) | A(4) | A(10) | A(4) | |||
Примечание. Правильность значений в таблице соответствия можно проверить с помощью алгоритма перевода чисел из десятичной системы счисления (см. стр. ).
Разобьём решение данной задачи на подзадачи. Рассмотрим отдельно операции умножения числа 123(4) на 3(4), 2(4) и 1(4).
Умножим 3(4) на последнюю цифру числа 123(4) (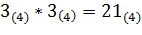 
). Цифру 1(4) записываем в нулевой разряд результата, цифру 2(4) переносим в более старший разряд (см. Рисунок ). Далее умножим 3(4) на вторую цифру числа 123(4) ( 
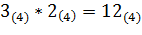). Складываем результат умножения цифрой 2(4), перенесенной из младшего разряда ( 
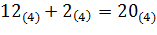). Последнюю цифру 0(4) результата записываем в первый разряд, цифру 2(4) переносим для суммирования в более старший разряд. Далее умножаем 3(4) на первую цифру числа 123(4) ( 
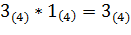). Результат умножения складываем с цифрой 2(4) ( 
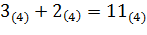). Цифру 1(4) записываем во второй разряд результата, другую цифру 1(4) переносим в третий разряд результата. На этом этапе вычисления закончены.
Рисунок
Аналогичные действия с помощью таблиц … производим при умножении 123(4) на 2(4) и 123(4) на 1(4).
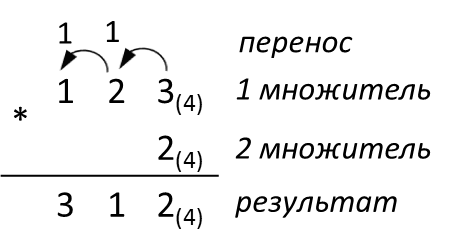
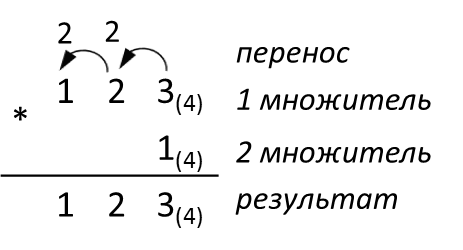
Рисунок Рисунок
Закончив умножения, сложим все полученные промежуточные результаты (Рисунок ). В конечном итоге получаем 123(4)*123(4) = 22121(4).
Рисунок
Переходим к делению. Деление «углом» также можно выполнять в любой системе счисления. Деление столбиком (также известное как деление уголком) — стандартная процедура в арифметике, предназначенная для деления простых или сложных многозначных чисел за счёт разбивания деления на ряд более простых шагов. [Википедия] В общем, операцию деления можно разложить на операции сравнения, умножения и вычитания.
Введем обозначения для чисел: делимое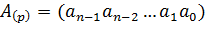 
, делитель 
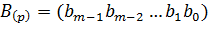, частное – 
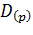, промежуточная разность (остаток) – 
.
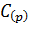Рассмотрим алгоритм деления. Шаги алгоритма будем нумеровать индексом j = 0,1,2… .
Шаг 1. Сравнение. На данном шаге определяется неполное делимое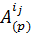 
, ij Î(0..n-1).
a. j=0. В левой части исходного числа A(p), начиная со старшего бита, необходимо выделить подстроку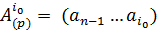 
, которую мы назвали неполным делимым, удовлетворяющую следующему условию: 
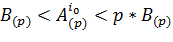. Очевидно, что если существует 
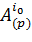, такое что 
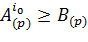, то при целочисленном делении можно получить частное большее или равное 1.
b. j¹0. Если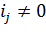 
, то для нахождения неполного делимого 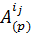необходимо дополнить строку остатка 
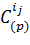справа неиспользованными цифрами исходного числа A(p).
.
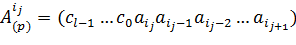Шаг 2. Умножение. Найти множитель rj, удовлетворяющий следующему условию: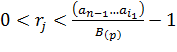 
.
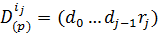
Шаг 3. Вычитание. Определить разность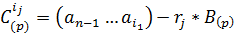 
.
Шаг 4. Проверка условия завершения вычислений. Если оба условия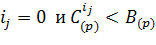 
истинны, то при делении делимого A(p) на делитель B(p) получено частное 
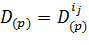и остаток 
.
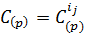Пример.Разделить 1201021(3) на 102(3). Для удобства вычислений составим таблицу соответствия чисел десятичной и троичной систем счисления.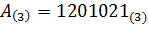 
, 
.
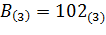1. j=0. Очевидно, что i0=3 и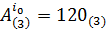 
. Далее,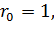 
, 
. 
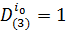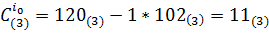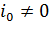
2. j=1. i1=2 и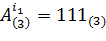 
. Далее,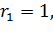 
, 
.
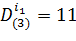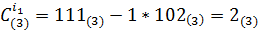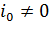
3. j=2. i2=1 и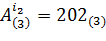 
. Далее,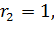 
, 
.
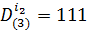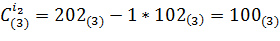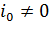
4. j=3. i3=0 и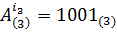 
. Далее,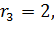 
, 
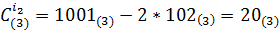. Так как 
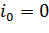и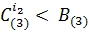 
, следовательно вычисления закончены. Результат: 1201021(3) : 102(3) = 1112(3) и 1201021(3) mod 102(3) = 20(3)
| A(10) | A(3) | A(10) | A(3) | A(10) | A(3) | A(10) | A(3) | |||
Арифметические операции в двоичной системе счисления
Рассмотрим двоичную систему счисления, так как все вычисления в компьютере производятся именно в двоичной системе счисления. Главное достоинство двоичной системы – простота алгоритмов сложения, вычитания, умножения и деления.
По сравнению с другими системами счисления в двоичной системе наиболее просто реализуются процессы выполнения арифметических операций над числами. В табл. 2 показаны правила выполнения операций сложения, вычитания, умножения и Деления одноразрядных двоичных чисел.
| Сложение | Умножение | Вычитание | Деление | Сложение Å |
| 0+0=0 0+1=1 1+0=1 1+1=10 | 0*0=0 0*1=0 1*0=0 1*1=1 | 0-0=0 1-0=1 1-1=0 0-1=1* | 0:1=1 1:1=1 | 0Å0=0 0Å1=1 1Å0=1 1Å1=0 |
Приведем несколько примеров.
1. Сложить два числа в двоичной системе счисления: 11100110(2)+11011101(2).
2. Выполнить операцию вычитания в двоичной системе счисления: 11100110(2)-11011101(2).
3. Выполнить операцию умножения в двоичной системе счисления: 11100110(2) * 1111(2).
Напоминаем, что при умножении столбиком множимое число умножается на каждую цифру второго числа. Все полученные промежуточные результаты затем складываются. Стрелками на схеме обозначены переносы единиц в более старшие разряды.
Как видно из приведенных примеров, операция деления может быть представлена как операции сдвига и суммирования.
11100110*1111=
= 1*11100110 + 10*11100110 + 100*11100110 + 1000*11100110 = 11100110 + 111001100 + 1110011000 + 11100110000 = 110101111010
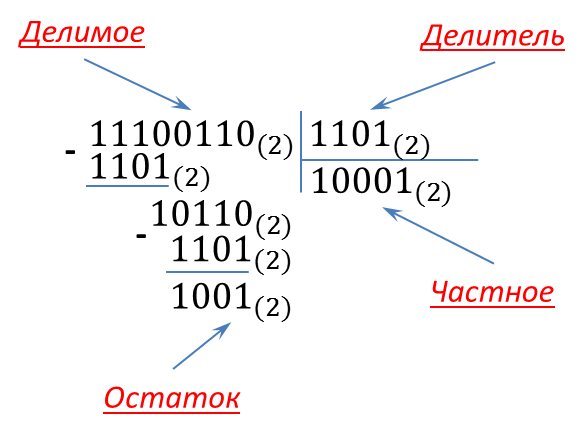
4. Выполнить операцию деления в двоичной системе счисления: 11100110(2) : 1101(2).
Деление в двоичной системе производится вычитанием делителя со сдвигом вправо, если остаток больше нуля. Как видно из приведенных примеров, операция деления может быть представлена как операции сравнения, сдвига и суммирования.
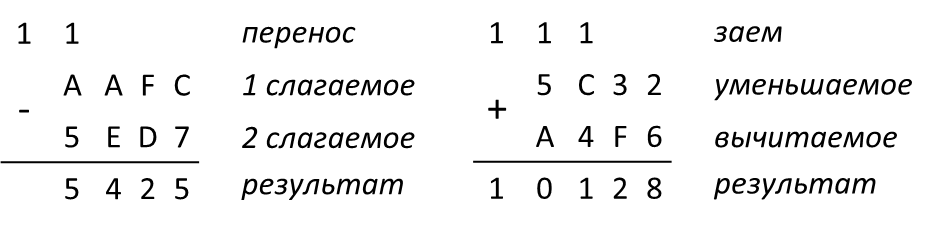
Шестнадцатеричная и восьмеричная системы счисления при производстве вычислений несколько сложнее, чем двоичная, в частности, в том, что касается правил переносов в старшие разряды (заёмов из старших разрядов). Главное здесь — помнить следующие равенства:
1 + F = 10(16) и
1+7 = 10(8)
Пример приведен на рис. 6.2:
Варианты лабораторной работы
1. а) Деление 2-х чисел в системе счисления, заданной вариантом. Двоичная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 4 Байт.
2. а) Деление 2-х чисел в системе счисления, заданной вариантом. Троичная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 4 Байта.
3. а) Деление 2-х чисел в системе счисления, заданной вариантом. Двоичная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 6 Байт.
4. а) Перевод числа из системы счисления, заданной вариантом, в десятичную систему счисления. Двоичная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере: -3455,235545. Объем памяти для записи числа - 6 Байт.
5. а) Перевод числа из системы счисления, заданной вариантом, в десятичную систему счисления. Четверичная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 6 Байт.
6. а) Перевод числа из системы счисления, заданной вариантом, в десятичную систему счисления. Восьмеричная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 6 Байт.
7. а) Перевод числа из системы счисления, заданной вариантом, в десятичную систему счисления. Шестнадцатеричная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 4 Байта.
8. а) Сложение 2-х чисел в системе счисления, заданной вариантом. Двоичная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 4 Байта.
9. а) Сложение 2-х чисел в системе счисления, заданной вариантом. Четверичная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 6 Байт.
10. а) Сложение 2-х чисел в системе счисления, заданной вариантом. Восьмеричная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 6 Байт.
11. а) Сложение 2-х чисел в системе счисления, заданной вариантом. Шестнадцатеричная.
Б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 4 Байта.
12. а) Вычитание 2-х чисел в системе счисления, заданной вариантом . Двоичная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 6 Байт.
13. а) Вычитание 2-х чисел в системе счисления, заданной вариантом . Четверичная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 4 Байта.
14. а) Вычитание 2-х чисел в системе счисления, заданной вариантом . Восьмеричная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 6 Байт.
15. а) Вычитание 2-х чисел в системе счисления, заданной вариантом. Шестнадцатеричная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 4 Байта.
16. а) Умножение 2-х чисел в системе счисления, заданной вариантом. Двоичная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 6 Байт.
17. а) Умножение 2-х чисел в системе счисления, заданной вариантом. Четверичная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере: -763,200345. Объем памяти для записи числа - 4 Байта.
18. а) Умножение 2-х чисел в системе счисления, заданной вариантом. Восьмеричная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 6 Байт.
19. а) Умножение 2-х чисел в системе счисления, заданной вариантом. Шестнадцатеричная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 4 Байта.
20. а) Перевод числа из 10 системы счисления в систему счисления, заданную вариантом. Четверичная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 4 Байта.
21. а) Перевод числа из 10 системы счисления в систему счисления, заданную вариантом. Восьмеричная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 6 Байт.
22. а) Перевод числа из 10 системы счисления в систему счисления, заданную вариантом. Шестнадцатеричная.
б) Запрограммировать перевод числа с плавающей запятой в его внутреннее представление в компьютере. Объем памяти для записи числа - 4 Байта.
Список литературы
1. Гашков С.Б. Системы счисления и их применение. (Серия: «Библиотека «Математическое просвещение»»). М.: МЦНМО, 2004. — 52 с.: ил.
2. Острейковский В.А. Информатика: Учеб. Пособие для студ. сред. проф. учеб. заведений. – М.: Высш.шк., 2001. – 319 с.: ил.
3. Петцольд Ч. Код. – М.: Издательско-торговый дом «Русская редакция», 2001. – 512 с.: ил.
4. Фомин С.В. Системы счисления. — М.: Наука, 1980. — (Популярные лекции по математике. Вып. 40).
5. Юров В.И. Assembler. Учебник для вузов. Изд-во «Питер». – 2010 г. – 638 с.
4. Лабораторная работа №3. Кодирование-декодирование
Цель лабораторной работы.Изучение методов помехоустойчивого и оптимального кодирования.
Общее задание. Написать программу, осуществляющую следующие преобразования с двоичным сообщением:
· Кодирование;
· Декодирование;
· Проверку на наличие ошибок в закодированном сообщении.
Тип кодирования определяется вариантом.
Ход работ.Для выполнения данной работы необходимо запрограммировать следующие этапы :
1. Этап кодирования.
a. Ввести
b. строку двоичных символов длины N – строка S. (Например: S = 010101111001)
c. Закодировать строку S с помощью метода кодирования, указанного в варианте на лабораторную работу – строка S’.
2. Этап декодирования.
a. Ввести строку двоичных символов длины M – строка D. При этом строка D может быть следующей:
i. D=S’ (передача произошла без ошибок);
ii. D<>S’ (передача произошла с ошибками).
b. Декодировать полученную строку D с помощью метода декодирования, указанного в варианте, если строка передана без ошибок
c. Обнаружить и исправить ошибку (или ошибки) передачи по каналу и декодировать полученную строку D с помощью метода декодирования, указанного в варианте.
3.Для проверки работоспособности программ необходимо предоставить не менее 5-ти контрольных примеров.