Задача 2.2. Расчет статически определимых систем на прочность
Абсолютно жесткий брус, шарнирно закрепленных в одной точке, удерживается в горизонтальном положении с помощью деформируемого стержня заданной площади поперечного сечения А. Определить из условия прочности деформируемого стержня величину допускаемой нагрузки [F].
Исходные данные в табл. 2.2.1 и 2.2.2.
Таблица 2.2.1. Исходные данные вариантов
| 1. Варианты схем | 2. Варианты прочностных характеристик | 3. Варианты линейных и угловых размеров и площадей | |||||||
| № вар. | № схемы | № вар. | 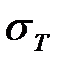 , МПа , МПа | 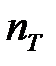 | № вар. | a, м | k | α, град | А, м2 |
| Вариант 0 | 1,6 | 0,4 | 1,5 | 6·10-4 | |||||
| Вариант 1 | 2,0 | 0,6 | 5·10-4 | ||||||
| Вариант 2 | 1,4 | 0,5 | 0,5 | 3·10-4 | |||||
| Вариант 3 | 1,7 | 1,3 | 1,3 | 4·10-4 | |||||
| Вариант 4 | 1,3 | 0,7 | 2,8 | 7·10-4 | |||||
| Вариант 5 | 2,0 | 1,0 | 0,8 | 4·10-4 | |||||
| Вариант 6 | 1,9 | 0,8 | 1,8 | 2·10-4 | |||||
| Вариант 7 | 1,5 | 0,9 | 2,1 | 9·10-4 | |||||
| Вариант 8 | 2,0 | 1,1 | 3,1 | 8·10-4 | |||||
| Вариант 9 | 1,8 | 0,3 | 3,5 | 3·10-4 |
Таблица 2.2.2. Схемы стержневых систем
 |  |
 |  |
 |  |
 |  |
 |  |
Министерство образования и науки Российской Федерации
Тольяттинский государственный университет
Институт машиностроения
Кафедра «Нанотехнологии, материаловедение и механика»
Расчетно-проектировочная работа №3
по дисциплине «Сопротивление материалов»
«Расчет на прочность и жесткость при изгибе»
Вариант №______
Студент _________________________
Группа _______________
Преподаватель ___________________
Оценка _________________________
«____» _______________20___г.
Тольятти 20___
Задача 3.1. Определение главных центральных моментов инерции сложного сечения
Сечение сложной формы является поперечным сечением некоторой нагруженной конструкции. Для расчета в дальнейшем этой конструкции на прочность и жесткость необходимо определить положение главных центральных осей и значения главных центральных моментов инерции сложного сечения.
Исходные данные взять в табл. 3.1.1 и 3.1.2.
План решения
1. Разбить сложное сечение на простейшие составляющие и определить положение их центров тяжести.
2. Выбрать вспомогательную ось отсчета, относительно которой определить координаты центров тяжести простейших составляющих сложного сечения.
3. Найти координату центра тяжести всего сложного сечения и провести его главные центральные оси.
4. Определить значения главных центральных моментов инерции сложного сечения в долях параметра а.
Таблица 3.1.1. Исходные данные вариантов
| Первая цифра варианта | Вторая цифра варианта | Третья цифра варианта | ||||
| № вар. | № схемы сечения | № вар. | k1 | k2 | № вар. | k3 |
| Вариант 0 | 1,0 | 0,30 | ||||
| Вариант 1 | 0,9 | 0,10 | 0,26 | |||
| Вариант 2 | 0,8 | 0,20 | 0,22 | |||
| Вариант 3 | 0,7 | 0,20 | ||||
| Вариант 4 | 0,6 | 0,3 | 0,30 | |||
| Вариант 5 | 0,6 | 0,2 | 0,32 | |||
| Вариант 6 | 0,7 | 0,1 | 0,18 | |||
| Вариант 7 | 0,9 | 0,36 | ||||
| Вариант 8 | 0,4 | 0,3 | 0,16 | |||
| Вариант 9 | 0,5 | 0,40 | 0,24 |
Таблица 3.1.2. Схемы сечений
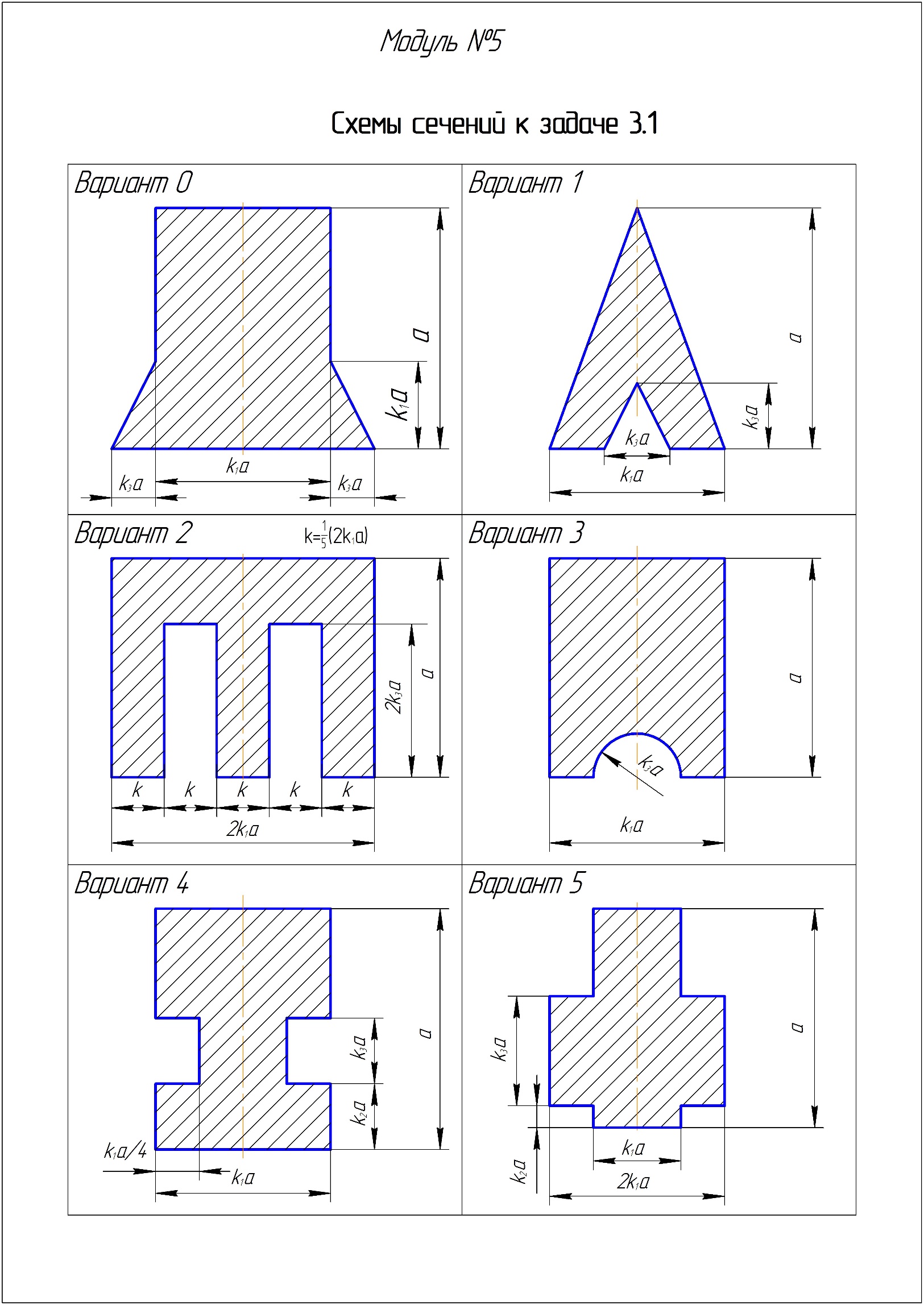
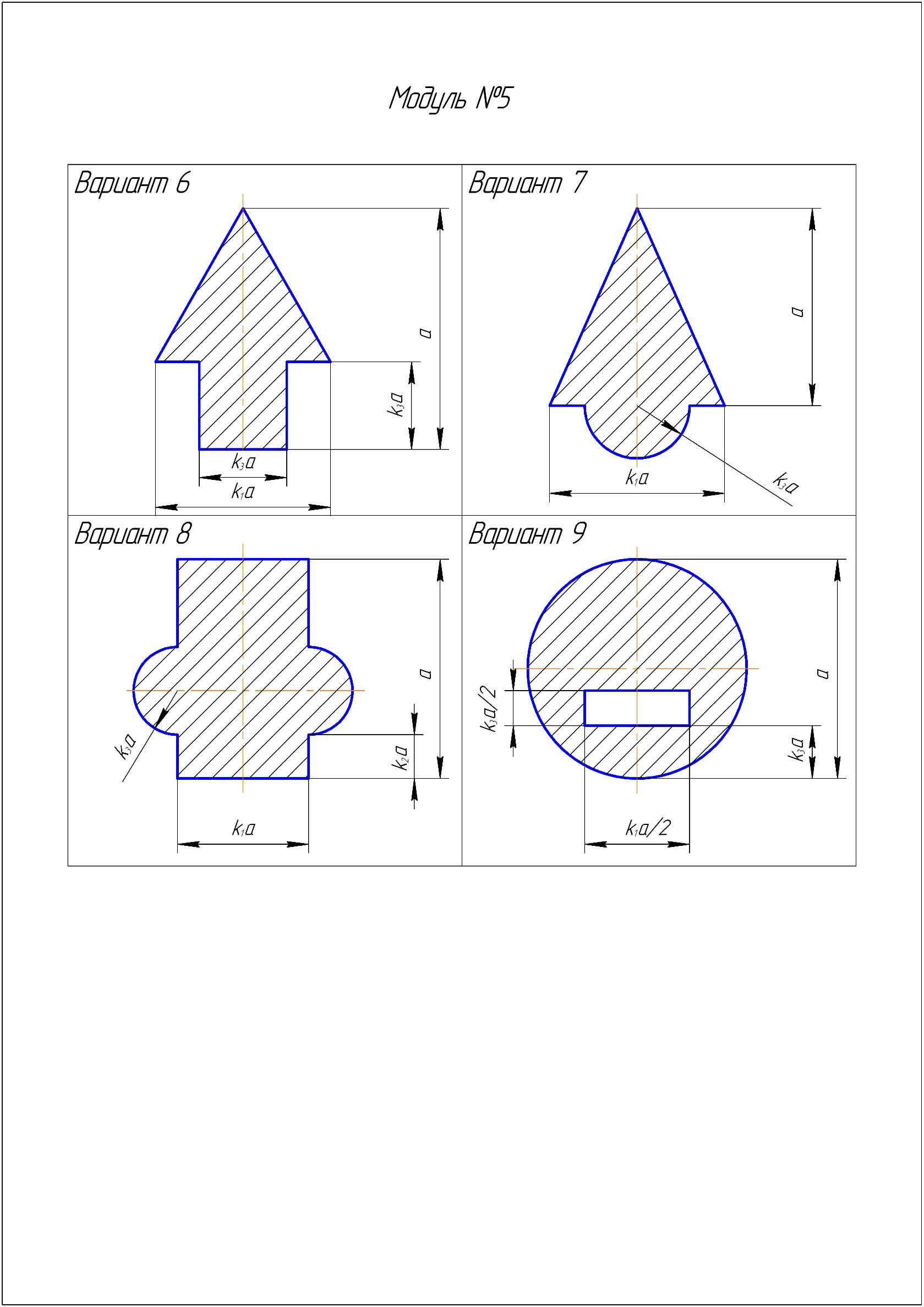
Задача 3.2. Расчет на прочность и жесткость балок при плоском поперечном изгибе
План решения
1. Вычертить в масштабе балку на двух опорах с построенными эпюрами Qy и Mx (взять из РПР №1, задача 1.3, схема №2).
2. Для балки, изготовленной из пластичного материала, подобрать из условия прочности двутавровое, прямоугольное (h/b = 2) и круглое сечения, приняв [s] = 160 МПа. Дать заключение о рациональности формы сечения по расходу материала.
3. Для балки, изготовленной из хрупкого материала, определить из условия прочности характерный размер [а] сложного поперечного сечения (из задачи 3.1), предварительно решив вопрос о его рациональном положении.
4. Определив перемещения незакрепленных граничных сечений, изобразить приближенный вид оси изогнутой балки и провести проверку жесткости балки двутаврового сечения, приняв [ 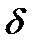 ] = (0,0005…0,001)·l (где l – расстояние между опорами).
] = (0,0005…0,001)·l (где l – расстояние между опорами).
Таблица 3.2. Характеристики прочности для хрупкого материала
| Третья цифра варианта | ||
| № вар. | 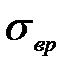 , МПа , МПа | 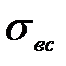 , МПа , МПа |
Общие данные: 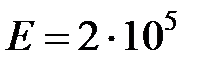 МПа – модуль упругости первого рода;
МПа – модуль упругости первого рода;
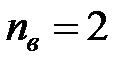 – коэффициент запаса по прочности.
– коэффициент запаса по прочности.
