Некоторые полезные статистические функции табличного процессора Microsoft Excel

=ДИСП(Ряд)

Вычисляет дисперсию выборочных данных, содержащихся в интервале Ряд.

=ДИСПР(Ряд)

Вычисляет дисперсию генеральной совокупности данных, содержащейся в интервале Ряд.

=ДОВЕРИТ(Значимость;СтандОткл;ЧислоНаблюдений)

Вычисляет одностороннюю предельную ошибку среднего для нормально распределённой совокупности данных для уровня доверия, равного (1–Значимость), при заданных среднеквадратичном отклонении СтандОткл и численности наблюдений ЧислоНаблюдений.

=КОРРЕЛ(Ряд1;Ряд2)

Вычисляет коэффициент парной линейной корреляции по Пирсону для двух совокупностей данных, содержащихся в интервалах Ряд1 и Ряд2. Число ячеек в обоих рядах должно быть одинаковым. Все они должны содержать числовые данные (пустые ячейки не допускаются).

=МАКС(Ряд)

Находит наибольшее значение среди данных, содержащихся в интервале Ряд.

=МЕДИАНА(Ряд)

Находит медиану совокупности данных, содержащихся в интервале Ряд.

=МИН(Ряд)

Находит наименьшее значение среди данных, содержащихся в интервале Ряд.

=МОДА(Ряд)

Находит модальное значение совокупности данных, содержащихся в интервале Ряд, если таковое существует.

=НАИБОЛЬШИЙ(Ряд;Ранг)

Находит среди данных в интервале Ряд значение, имеющее порядковый номер Ранг, если значения пронумеровать в порядке убывания.

=НАИМЕНЬШИЙ(Ряд;Ранг)

Находит среди данных в интервале Ряд значение, имеющее порядковый номер Ранг, если значения пронумеровать в порядке возрастания.

=ПЕРСЕНТИЛЬ(Ряд;Персентиль)

Находит значение, которое вместе с другими не превышающими его значениями образует требуемую Персентиль (указываемую в долях) совокупности данных в интервале Ряд.

=РАНГ(Число;Ряд;Порядок)

Определяет ранг значения Число в совокупности данных, содержащейся в интервале Ряд, по возрастанию (если значение Порядок равно нулю либо опущено) или по убыванию (если значение Порядок указано и не равно нулю). Значение Число обязательно должно присутствовать в интервале Ряд.

=СКОС(Ряд)

Вычисляет коэффициент асимметрии для эмпирического распределения, представленного данными в интервале Ряд.

=СРЗНАЧ(Ряд)

Вычисляет среднее арифметическое по данным интервала Ряд.

=СРЗНАЧЕСЛИ(Ряд,Условие)

Вычисляет среднее арифметическое для данных интервала Ряд, отвечающих критерию Условие. Критерий представляет собой текст вида ">2", "<-3,14159", где число может быть произвольным, либо ссылку на ячейку, содержащую формулу, результатом вычисления которой является подобное текстовое значение.

=СРЗНАЧЕСЛИМН(Ряд,Условия)

Вычисляет среднее арифметическое для данных интервала Ряд, отвечающих одновременно всем критериям, хранящимся в интервале Условия. Каждый критерий представляет собой текст вида ">2", "<-3,14159", где число может быть произвольным. Поддерживается не всеми версиями Excel.

=СТАНДОТКЛОН(Ряд)

Вычисляет среднеквадратическое отклонение выборочных данных, содержащихся в интервале Ряд.

=СТАНДОТКЛОНП(Ряд)

Вычисляет среднеквадратическое отклонение данных генеральной совокупности, содержащейся в интервале Ряд.

=СЧЁТ(Ряд)

Определяет число значений в интервале Ряд.

=СЧЁТЕСЛИ(Ряд;Условие)

Определяет число значений в интервале Ряд, отвечающих критерию Условие. Критерий представляет собой текст вида ">2", "<-3,14159", где число может быть произвольным, либо ссылку на ячейку, содержащую формулу, результатом вычисления которой является подобное текстовое значение.

=СЧЁТЕСЛИМН(Ряд;Условия)

Определяет число значений в интервале Ряд, отвечающих одновременно всем критериям, хранящимся в интервале Условия. Каждый критерий представляет собой текст вида ">2", "<-3,14159", где число может быть произвольным. Поддерживается не всеми версиями Excel.

=ЧАСТОТА(РядДанных;Границы)

Вычисляет массив значений, каждое из которых означает число наблюдений из интервала РядДанных, относящихся к классу, задаваемому данными в интервале Границы.

Для использования функции следует выделить на одну ячейку больше, чем содержится их в интервале Границы, набрать содержащую её формулу и нажать сочетание клавиш [Ctrl]+[Shift]+[Enter]. В первой ячейке выделенного интервала отобразится число значений, которые не больше первого значения в интервале Границы; во второй — число значений между первым и вторым значениями в интервале Границы (исключая нижнюю границу и включая верхнюю) и т.д.; в последнем — значения, превышающие наибольшее значение в интервале Границы.

Значения в интервале Границы должны быть упорядочены по возрастанию. Пустые ячейки и текстовые значения игнорируются.

=ЭКСЦЕСС(Ряд)

Вычисляет коэффициент эксцесса для эмпирического распределения, представленного данными в интервале Ряд.

Численное интегрирование

Необходимость вычисления определённых интегралов при решении задач системного анализа по методике, положенной в основу настоящего практикума, возникает, например, при определении ошибки оценки вероятности события по результатам наблюдений, при отыскании квантилей либо (в некоторых случаях) при проверке гипотезы о законе распределения случайной величины.

Для вычисления определённых интегралов в MathCad достаточно ввести требуемый интеграл в виде формулы. Чтобы ввести знак интеграла, следует нажать клавишу [&]. Например, вычисление формулы

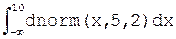
даст тот же результат, что и формулы pnorm(10,5,2), а именно 0,99379.

Excel не имеет встроенных возможностей численного интегрирования. Если лабораторные работы выполняются в Excel, вычисление определённых интегралов можно осуществлять любым известным методом, например, методом трапеций или методом Симпсона. Описание соответствующих алгоритмов можно найти в сети Интернет либо в учебной литературе по численным методам[21].

СОДЕРЖАНИЕ

Введение.............................................................................................................. 3

методические указания преподавателю............................................................. 5

Постановка задачи.............................................................................................. 8

Теоретическая часть.................................................................................... 8

Задание....................................................................................................... 12

Варианты заданий для лабораторного практикума................................ 13

Тема 1. Спецификация первого уровня аграрной производственной системы 14

Теоретическая часть.................................................................................. 14

Практическая часть................................................................................... 18

Тема 2. Приведение числовых переменных к дискретной форме.................. 21

Теоретическая часть.................................................................................. 21

Практическая часть................................................................................... 23

Тема 3. Представление знаний о структуре системы в форме условных вероятностей. Проверка существенности и независимости переменных.... 25

Теоретическая часть.................................................................................. 25

Практическая часть................................................................................... 29

Тема 4. Спецификация второго уровня аграрной производственной системы 33

Теоретическая часть.................................................................................. 33

Практическая часть................................................................................... 35

Тема 5. Тестирование двухуровневой модели................................................ 38

Теоретическая часть.................................................................................. 38

Практическая часть................................................................................... 41

ПРИЛОЖЕНИЯ................................................................................................ 45

1. Основные статистические распределения............................................. 45

2. Проверка согласованности эмпирического и теоретического распределений с помощью критерия c2............................................... 60

3. Проверка статистических гипотез относительно многовершинных распределений........................................................................................ 64

4. Проверка независимости факторов с помощью критерия c2............. 65

5. Проверка существенности связи между переменными с помощью однофакторного дисперсионного анализа........................................... 67

6. Процедура расчёта энтропии, снимаемой с переменной информацией о значении другой переменной................................................................ 68

7. Некоторые полезные статистические функции табличного процессора Microsoft Excel....................................................................................... 70

8. Численное интегрирование................................................................... 73

[1] Например, следует учитывать, что трудоёмкость предварительного статистического анализа числовой переменной значительно выше, чем нечисловой. Преподавателю рекомендуется контролировать равномерность распределения учебной нагрузки между студентами в рабочих группах, а при необходимости своевременно предупреждать студентов как о чрезмерности намеченного объёма работ, так и о его недостаточности для отличной (хорошей, удовлетворительной) рейтинговой оценки.

[2] Например, информация о них поступает лишь тогда, когда выходная переменная уже известна достоверно.

[3] В статистико-математических и эконометрических приложениях следует различать понятия «оценка» (estimate – англ.) — суждение о величине параметра, не поддающегося непосредственному наблюдению, на основе и «оценивание» (estimation– англ.) — процесс получения оценки.

[4] Фактор, требующий представления в векторной форме, должен рассматриваться как набор факторов, соответствующих каждому компоненту вектора.

[5] Как правило, процедура измерения приводится в форме ссылки на источник, в котором она описана.

[6] Всеми необходимыми возможностями для этого обладают табличные процессоры.

[7] Предполагается, что одна страница содержит не более 40 строк по 66 символов.

[8] В ряде случаев для таких переменных гипотеза о нормальном распределении может быть приемлемой, если вероятность отрицательных значений согласно теоретическому распределению исчезающе мала.

[9] При гамма-распределении результаты оценки тесноты связи при посредстве дисперсионного анализа содержат ошибку, величина которой, однако, для большинства практических приложений не слишком велика.

[10] Если наблюдений больше 30 — можно использовать нормальное распределение, которое является пределом распределения Стьюдента при бесконечном числе наблюдений.

[11] За исключением тех редких случаев, когда оно оказывается частным случаем бета-распределения.

[12] За исключением тех редких случаев, когда оно оказывается частным случаем бета-распределения.

[13] Например, если коровы массой менее 400 и более 520 кг выбраковываются из основного стада, то при проверке гипотезы о согласии распределения живой массы коров с бета-распределением значения a=400, b=520 будут приняты обоснованно. Если же верхняя граница массы для выбраковки не установлена, достаточных оснований для моделирования эмпирического распределения живой массы с помощью бета-распределения нет.

[14] Эту пороговую вероятность называют уровнем доверия, или доверительной вероятностью.

[15] В последнем случае результаты обычно требуют перепроверки с привлечением новых наблюдений.

[16] См. формулы для определения значений параметров распределений при известных средней и дисперсии в Приложении 1.

[17] В учебных заданиях данного практикума разрешается смягчать эти требования в соответствии с указаниями преподавателя, обязательно отмечая в отчёте, что результат проверки гипотезы о согласии теоретического и эмпирического распределений недостоверен по причине недостаточной численности имеющихся наблюдений.

[18] Алгоритм расчёта приведён, например, в издании: Красс М.С., Чупрынов Б.П. Математические методы и модели для магистрантов экономики: Учеб. пособие. СПБ.: Питер, 2006. — С. 171-172.

[19] При большом числе входных переменных влияние каждой из них может быть весьма слабым. В этом случае при использовании однофакторного дисперсионного анализа в целях определения набора входных переменных, включаемых в модель, следует использовать уровни доверия, очень близкие к единице.

[20] Для целей данного практикума можно принять его равным 0,3.

[21] Численные методы / Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. 4‑е изд. М.: БИНОМ. Лаборатория знаний, 2006.