Функционирования тормоза откатных частей

Проектный расчет тормоза, как известно, сводится к определению таких его конструктивных параметров, при которых обеспечиваются заданные режимы торможения откатных частей при откате и накате. Поскольку спектр внешних условии функционирования тормоза весьма широк, выходные свойства конструкции (параметры состояний) отличаются нестабильностью. Проектная оценка выходных свойств тормоза обычно проводится решением обратных задач отката— наката путем просчета так называемых предельных диаграмм. Однако искусственный перебор ситуаций на границах возможных областей изменения параметров внешней среды зачастую не выявляет предельных состояний анализируемых процессов, так как последние могут иметь место не на границах области изменения варьируемых параметров, а где-либо внутри ее.

Для выявления предельных состояний процесса отката— наката и функционирования тормоза приходится привлекать методы оптимального управления. При этом в качестве функций управления выступают конструктивные параметры тормоза и режимы эксплуатации орудия, нестабильность которых из-за влияния внешней среды приводит к нестабильности параметров состояния

у= ,

где — угол возвышения ствола; k-—коэффициент гидравлического сопротивления тормоза; —сила давления пороховых газов на дно канала ствола; а(х)—рабочая площадь гидросопротивления; А — рабочая площадь поршня тормоза; — коэффициент статического трения в направляющих люльки или других подвижных сочленениях конструкции; П₀ — начальное усилие накатника; п — показатель процесса сжатия газа в накатнике; а — площадь технологического зазора между цилиндром и поршнем.

При необходимости в число управляемых параметров могут быть включены и другие переменные.

Стрельба на различных углах возвышения ствола, различ­ными зарядами и снарядами, изменение температуры рабочей жидкости тормоза, технологический разброс конструктивных размеров, эксплуатационный износ и другие обстоятельства накладывают на перечисленные функции управления двусторонние ограничения :

; (t);

Связь между независимыми параметрами управления и зависимыми параметрами состояния тормоза устанавливается математической моделью динамики движения откатных частей и гидромеханики функционирования тормоза:

M₀x:=P_кн(t,y)-R(x,x,y),

R (х, х, у) = П (х, у) + [Ф (х, х, у) + R_f(y)] sign x -Q₀ sin ,

где х — путь движения откатных частей, t— время, R — сила сопротивления откату, П — упругое усилие накатника, Ф — гидродинамическое сопротивление тормоза, Rf — суммарное статическое сопротивление в люльке и уплотнениях, Mo(Qo) — масса (вес) откатных частей. В простейших случаях решение дифференциального уравнения движения откатных частей получают методами последовательных сближений. При реализации задачи на ЦВМ пользуются стандартными программами численного интегрирования.

Задача поиска оптимальных режимов работы тормоза, соответствующих экстремальным значениям параметров состояния, в принятых обозначениях формулируется следующим образом: найти такие значения вектора параметров управления которые минимизируют или максимизируют критерий (целевую функцию) Q ( ) в области R, определяемой ограничениями

min {Q(y):y 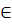R; R= },

где значения j-й управляемой переменной, характеризующие область ее возможных изменений.

Целевые функции Q(y) могут иметь смысл тех или иных параметров состояния, по которым судят о качестве проектируемой конструкции тормоза:

Q(y) = R(y),

где R(y)—сила сопротивления откату или равнодействующая накату, λ(у) —длина отката, v_k(y) —скорость откатных частей в k-й интересующей проектировщика точке (в момент срабатывания механизма автоматики, при подходе к буферу наката, в момент наибольшей скорости отката или наката и т. п.), р(у) — давление в рабочих полостях тормоза, t_m —время движения откатных частей на т-х характерных участках (время отката, время наката и т. п.).

Задача нахождения экстремальных значений параметров состояния тормоза не может быть реализована классическими (аналитическими) методами из-за нелинейности, невыпуклости и большой размерности последней. Приходится использовать методы математического программирования (численной оптимизации). Заметим также, что задача в значительной мере усложняется еще и тем, что среди линейных ограничений на параметры управления у присутствует нелинейное технологическое ограничение на функцию площади гидросопротивлений тормоза а (х). Возможные пути реализации функции управления процессом движения откатных частей и ограничений на нее рассмотрены и проанализированы И. С. Кореневым:

—перебор траекторий а (х) с заданным интервалом, огра­ниченный возможной шириной технологического коридора (рис. 4.8, о);

—сканирующий просмотр технологического коридора с помощью периодической функции

а(х) = а_ср(х) + А (х) sin х,

где аср(х)—среднее значение площади гидросопротивлений, А(х)—ширина технологического коридора, — частота просмотра (рис. 4.8, б);

—стохастическая аппроксимация, учитывающая статические свойства случайной функции а(х): математические ожидания М_х[а(х)], дисперсии D_x[a(x)], корреляционную функцию К_х(х, х'), закон распределения площади гидросопротивлений по ширине технологического коридора f_x[a(x)] (рис. 4.8,в) ;

—аппроксимация функции а(х) и ограничений рядом дискретных значений. Здесь а(х) заменяется рядом дискрет­ных значений, на каждое из которых наложены двусторонние линейные ограничения (рис. 4.8, г).

Следует отметить, что первые два способа наиболее просты, однако не исключают потерю экстремальных ситуаций, так как реальные траектории а{х) отличаются от предлагаемых здесь аппроксимаций. Стохастический подход наиболее достоверен, однако требует наличия статистической информации о поведении функции а(х), сбор и обработка

Рис. 4.8. Реализация функции управления процессом движения откатных частей и ограничений на нее: а — ограниченный перебор траекторий; б — аппроксимация периодической функцией; в — стохастическая аппроксима­ция; г— аппроксимация дискретным рядом

которой — задача сама по себе достаточно сложная, трудоемкая, а в

случаев практически недостижимая. Алгоритмы стохастического программирования, кроме того, требуют больших затрат машинного времени. Наиболее приемлемым поэтому, пока считается дискретный подход. Последний, правда, увеличивает размерность задачи на число дискретизаций функции а(х). Количество назначаемых дискретных точек, аппроксимирующих а(х), определяет точность решаемой задачи, зависит от величины производной da(x)/dx, обусловленной технологическим процессом изготовления формирующих гидросопротивления деталей тормоза.

В качестве примера рассмотрим результаты решения оптимизационной задачи по оценке наибольшей силы сопротивлений откату 125-мм танковой пушки. В число управляемых переменных было включено пять параметров: у1 = k— коэффициент гидравлического сопротивления тормоза, у₂ = = А — рабочая площадь поршня, y3(x)=a(x)—площадь гидросопротивлений, у4 = — угол возвышения ствола, у5= а — площадь кольцевого зазора между рубашкой поршня и внутренней поверхностью цилиндра. Функция цели

Q(y) = R(x,x,y1,y2,y3,y4,y5)

Учитывая возможный разброс температур рабочей жидкости тормоза,

Из-за технологических допусков на изготовление деталей и эксплуатационного износа

Углы возвышения ствола варьировались в заданном диапазоне

Функция у3(х) аппроксимировалась четырнадцатью дискретными точками, на каждую из которых накладывались ограничения в соответствии с заданными допусками на изготовление и износ регулирующих деталей тормоза (веретена и регулирующего очка) (рис. 4.9):

Требовалось в заданной системе ограничений определить оптимальный вектор параметров управления у, при котором сила сопротивления откату принимает наибольшее значение

max (R(y1,y2,y4,y5,y3,…,y314) : }.

Задача решалась с помощью стандартной программы «метод наискорейшего спуска». Максимизируемый по R_mах вариант (R_max = 90470 кг, t_R max = 0,0384 с, x_R max =0,288 м, λ = 0, 320 м) имеет место при следующем сочетании параметров управления у:

у₁=1,2, у₂=118см², у₄ = 30°, y5= 0,492 см²,

у_3] = 3,98 см², у₃₂ = 3,99 см², у₃₃=4,5 см², у₃₄= 4,25 см,

y35= 3, 99 см², у36= 3,52 см², у₃₇ = 2,86 см², у38= 2,55 см²,

V₃₉ = 2, 25 см², у310 = 1, 87 см², y311 == 1, 4 см², у312=0, 78 см²,

У₃₁₃ = 0,16 см², у₃₁₄ = 0,16 см².

Рис. 4.9. Технологический допуск на функцию площади гидросопротивлений тормоза 125-мм танковой пушки

Характер приближений к оптимальному варианту в процессе итеративной процедуры поиска показан на рис. 4.10.