Выбор вариационного принципа.

Выбор вариационного принципа определяет основные неизвестные функции, через которые впоследствии устанавливаются остальные неизвестные. В задачах механики де- формируемого твердого тела используются следующие вариационные принципы [3]: принцип Лагранжа, в соответствии с которым варьируются перемещения; принцип Кас- тильяно (варьируются напряжения), принцип Рейсснера (варьируются перемещения и на- пряжения), принцип Ху-Вашицы (варьируются перемещения, напряжения и деформации). В практических расчетах чаще всего используется принцип Лагранжа.

Выбор аппроксимирующих функций.

При кусочно-непрерывной аппроксимации предполагается, что перемещения внутри элемента могут быть выражены через перемещения в его узлах. Эта связь описывается при помощи так называемых функций формы, которые аппроксимируют действительное

поле перемещений внутри элемента. От выбора аппроксимирующих функций в значи- тельной степени зависит точность решения. Эти функции должны удовлетворять следую- щим критериям:

- критерию полноты: при стремлении размеров элемента к нулю выбранные функции формы должны обеспечить любые простые значения.

- критерию совместимости: функции формы должны обеспечивать непрерывность пе- ремещений и ее производных до (n-1)-го порядка на границе между элементами (где n- порядок старшей производной в функционале энергии).

При выполнении этих критериев с увеличением числа конечных элементов, модели- рующих конструкцию, результаты расчета монотонно сходятся к точному решению. На- рушение критерия совместимости в ряде случаев приводит к достоверному результату, но сходимость в этих случаях не будет монотонной.

Реализация вариационного принципа.

На этом этапе осуществляется вычисление матриц жесткостей элементов и построение глобальной матрицы системы алгебраических уравнений и вектора узловых сил. Глобаль- ная матрица жесткости может быть получена несколькими методами:

- методом непосредственного сложения жесткостей;

- методом конгруэнтного преобразования;

- при помощи конечно-разностных операторов.

Учет граничных условий.

Полученная на основе указанных методов матрица жесткости является вырожденной, поскольку в соответствии с уравнениями равновесия заданной системы часть уравнений (для пространственных систем – шесть, а для плоских - три) окажутся взаимно зависимы- ми. Корректировка этой матрицы при учете граничных условий приводит к невырожден- ной системе линейных алгебраических уравнений.

Решение системы алгебраических уравнений.

Для решения системы алгебраических уравнений используются стандартные про- граммы, имеющиеся в математическом обеспечении ЭВМ, и специально подготовленные и лучшим образом учитывающие симметрию и структуру матрицы жесткости системы – редкозаполненность или ленточность.

Определение распределения полей искомых величин.

После определения узловых перемещений в соответствии с известными соотноше- ниями теории упругости могут быть определены деформации и напряжения.

САПР МЭМС устройств

Термин МЭМС является аббревиатурой для МикроЭлектроМеханических Систем. В этом контексте:

•―Микро‖ означает, что устройства являются экстремально маленькими с размерами порядка микрометров и меньше.

•―Электро‖ – включены некоторые электрические компоненты.

•―Механические‖ система выполняет какие-либо механические движения.

•―Системы‖ отражает тот факт, что все эти особенности объединены в одном корпус. МЭМС технология использует существующую микроэлектронную базу и инфра-

структуру для создания комплексных машин в микроскопическом масштабе. Обширные области применения таких устройств существуют в коммерческих и индустриальных сис- темах. Хорошо известные компоненты, такие как интегральные кремниевые датчики дав- ления, акселерометры, датчики движения нашли широкое применение в течение послед- них лет в автомобилестроении и промышленности.

МЭМС состоят из микроскопических электромеханических компонентов, однако не все инженеры проектировщики принимают во внимание, что почти все МЭМС устройства включают в себя несколько областей физики (мультифизичность multiphysics). Как мини- мум в устройстве есть электрические и механические части, описываемые соответствую- щей физической теорией. Также часто электрические и механические элементы являются сопряженными посредством теплофизических, электрохимических или других эффектов, что добавляет третий или четвертый физический эффект в систему.

Мультифизичная природа МЭМС устройств требует от разработчика широкого пони- мания и знаний в различных областях физики. Вследствие того, что некоторые эффекты на микроуровне являются новыми или проявляются отлично от эффектов на макроуровне инженеры должны обладать новой философией системного проектирования. При проек- тировании МЭМС устройств становится трудно разбивать проект на несколько частей, что являлось обычным при проектировании макроустройств, когда один инженер мог изучать механику, в то время как остальные концентрировались, например на электрических и те- пловых аспектах. Таким образом, инженер МЭМС является системным проектировщиком, оперирующим несколькими физическими областями одновременно и САПР должен по- зволять ему это делать.

Пионеры МЭМС проектирования в исследовательских и промышленных организаци- ях решили некоторые проблемы в области моделирования и проектирования. Они ис- пользовали существующее программное обеспечение для анализа поведения МЭМС уст- ройств с помощью численных методов (САПР основанный на МКЭ). В то же время оче- видна необходимость разработки и использования новых САПР, реализующих системный подход к проектированию МЭМС.

САПР, основанные на МКЭ.

Первые программные комплексы, в которых реализован метод конечных элементов, были разработаны в 60-х годах, например STRUDL-II, SAP-IV, NONSAP, ASKA, NASTRAN, SESAM-69 и другие [17]. Появлению этих универсальных программных сис- тем в силу особенностей метода конечных элементов предшествовало создание высоко- производительных электронно-вычислительных машин. Дальнейшее развитие МКЭ и не- обходимость в проведении расчетов конструкций на прочность способствовали дальней- шему развитию уже созданных программных комплексов и разработке новых. Были раз- работаны сотни программных комплексов, предназначенных для приближенного решения самых разнообразных задач не только из области механики деформируемого твердого те- ла, но и из таких областей как гидродинамика, акустика, электротехника и т.д. Наиболь- шее распространение из них получили [15]: ABAQUS, ADINA, ASKA/DYNAN, ANSYS

[1], MARC, MSC/NASTRAN [10], EUFEMI, COSMOS, HERCULE, MODULEF, SAP-7, LS- DYNA, COMSOL MULTIPHYSICS.

У каждой программы есть свои сильные и слабые стороны при расчете конкретной конструкции. Выбор программы расчета зависит от подготовленности пользователя в сво- ей научной области, типа решаемой задачи, типа доступной ЭВМ, размерности задачи и других факторов.

Современные комплексы программ, в которых используется МКЭ, позволяют полу- чать приближенные численные решения при расчете конструкций на статические и дина- мические нагрузки для широкого класса материалов с различными механическими харак- теристиками и поведением. Расчет конструкций на статические нагрузки может произво- диться с учетом физической и геометрической нелинейности, температурных полей, взаи- модействия с другими средами (например, с жидкостью). Производится расчет критиче- ских нагрузок, при которых конструкция или ее элементы теряют устойчивость, поведе- ния конструкции после потери устойчивости. МКЭ позволяет также определить нагрузки, при которых происходит разрушение конструкции. Учитываются такие свойства материа- ла как анизотропия, упругость, пластичность, текучесть. Учитываются также виды гео- метрической нелинейности: большие деформации и большие перемещения. Основными динамическими задачами являются: расчет собственных колебаний конструкции; динами- ческий отклик на нагрузку, зависящую от времени; распространение волн.

По мере роста потребления МЭМС устройств в универсальные пакеты, основанные на МКЭ (Ansys, Comsol) стали включать специально разработанные модули для модели- рования микромеханических устройств. На рис.1.3 приведена диаграмма, объясняющая использования пакета Ansys при проектировании устройств МСТ.

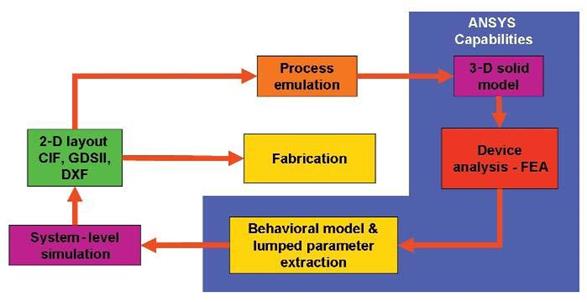
Рисунок 1.3. Возможности МКЭ пакетов по проектированию МЭМС [11].

Как видно из рисунка с помощью общих программных пакетов, основанных на МКЭ можно проводить трехмерное моделирование, МКЭ анализ микроустройств и создавать на

его основе поведенческие модели. За рамками этих пакетов остаются возможности проек- тирования и эмуляции техпроцессов, системного моделирования.