Применение производной для решения задач.

Цель работы

1. 1 Научиться применять производную для решения геометрических и физических задач

1.2 Научиться применять производную для приближённых вычислений

Ход работы

Вариант

Материальная точка движется прямолинейно по закону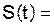

1.Найдите скорость в момент времени t = c.

2.Найдите ускорение в момент времени t = c.

3.Через сколько секунд после начала движения точка остановится?

4.Напишите уравнение касательной к графику функции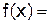

в точке с абсциссой x₀ = .

5.Найдите тангенс угла наклона к оси OX касательной графика функции 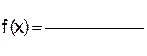, проходящей через точку с абсциссой .

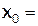6.Написать уравнение касательной к графику функции

в точке с абсциссой x₀ = .

7.Вычислите приближенное значение функции 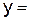при х =

8.Найти наибольшее и наименьшее значение функции

на отрезке [ ].

9.Закон прямолинейного движения тела задан уравнением: . Определите, в какой момент времени скорость движения тела будет наименьшей и найдите эту скорость.

10.Найти наибольшее и наименьшее значение функции

на отрезке [ ].

3. Результаты работы

ПРАКТИЧЕСКАЯ РАБОТА 16

Вычисление неопределённых интегралов

Цель работы

Научиться вычислять неопределённые интегралы

Ход работы

Вариант

Вычислить интегралы:

2.1.1.	2.1.13
2.1.2	2.1.14
2.1.3	2.1.15
2.1.4	2.1.16
2.1.5	2.1.17
2.1.6.	2.1.18
2.1.7	2.1.19
2.1.8	2.1.20
2.1.9	2.1.21
2.1.10	2.1.22
2.1.11	2.1.23
2.1.12	2.1.24

2.1.25 Скорость прямолинейного движения материальной точки задаётся формулой

v(t) =

Найдите закон движения S(t), если в момент времени t = с координата точки

равнялась .

2.1.26 Для функции у(х) = найдите первообразную , график которой проходит через точку М( ; )

Результаты работы

ПРАКТИЧЕСКАЯ РАБОТА 17

Вычисление определённых интегралов.

Цель работы

Научиться вычислять определённые интегралы

Ход работы

Вариант

Вычислить интегралы:

2.1.1.
2.1.2
2.1.3
2.1.4
2.1.5
2.1.6.
2.1.7
2.1.8
2.1.9.
2.1.10.

Результаты работы

ПРАКТИЧЕСКАЯ РАБОТА 18

Вычисление площадей плоских фигур с помощью

Определённого интеграла.

Цель работы

Научиться вычислять площади плоских фигур с помощью определённого интеграла

Ход работы

Вариант

Вычислить площадь фигуры, ограниченной линиями:

2.1.1.

2.1.2

2.1.3

2.1.4

2.1.5

Результаты работы

ПРАКТИЧЕСКАЯ РАБОТА 19

Решение задач на параллельность в пространстве.

Цель работы

Научиться решать задачи, применяя свойства параллельности прямых и плоскостей в пространстве

Ход работы

Вариант

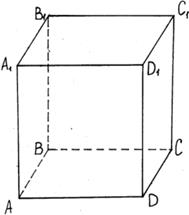
2.1.1 Дан прямоугольный параллелепипед АВСДА₁В₁С₁Д₁ .

Найдите две прямые, параллельные:

а)прямой __________________ _, б) плоскости ________________.

Найдите плоскости параллельные:

в) прямой _________________ г) плоскости _________________

д) Через точку М провести прямую, параллельную ____________

2.1.2 Через концы отрезка АВ и его середину М проведены параллельные прямые,

пересекающие некоторую плоскость в точках А₁, В₁, М₁. Найдите ____________

_______________________________________________________________________

_______________________________________________________________________

если отрезок АВ не пересекает плоскость.

2.1.3 Через концы отрезка АВ и его середину М проведены параллельные прямые,

пересекающие некоторую плоскость в точках А₁, В₁, М₁. Найдите ____________

_______________________________________________________________________

_______________________________________________________________________

если отрезок АВ пересекает плоскость.

2.1.4 Точка А - конец отрезка АВ лежит в плоскости. Через конец В и точку М,

принадлежащей отрезку АВ, проведены параллельные прямые, пересекающие

данную плоскость в точках В₁, М₁ соответственно. Найдите _________________

_______________________________________________________________________

_______________________________________________________________________

2.1.5 Дан треугольник АВС. Плоскость, параллельная прямой АС пересекает сторону АВ

этого треугольника в точке А₁, а сторону ВС в точке С₁. Найдите _______________

_______________________________________________________________________

_______________________________________________________________________

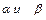2.1.6 Две плоскости параллельны между собой. Из точки М, лежащей по одну

сторону от них, проведены две прямые, пересекающие плоскость 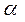в точках

А₁и А₂, а плоскость 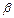в В₁ и В₂ соответственно. Найдите ___________________

_______________________________________________________________________

_______________________________________________________________________

2.1.3 Через точку М, лежащую между параллельными плоскостями 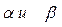, проведены

две прямые, пересекающие плоскость 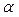в точках А₁и А₂, а плоскость 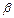в В₁ и В₂

соответственно. Найдите _________________________________________________

_______________________________________________________________________

_______________________________________________________________________

Результаты работы

Наши рекомендации

Применение ГИС для решения экономических задач и в сфере бизнеса

Базы данных и их применение для решения экономических задач

Применение термометрии скважин для решения геологических и технических задач

Применение дифференциальных уравнений первого порядка для решения задач

Применение производной для решения задач

Пояснить применение регрессионного анализа, применяемого для решения задач оптимизации.

Производная и ее применение для решения прикладных задач

ПРИМЕНЕНИЕ MathCAD ДЛЯ РЕШЕНИЯ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫХ ЗАДАЧ.

Применение теоретических положений в условиях выполнения упражнений и решения задач

Применение нейронных сетей для решения задач идентификации объектов управления

← Предыдущая страница | Следующая страница →