Вычислительная схема метода потенциалов

Шаг 1. Строим опорный план (методом северо-западного угла или методом минимальной стоимости) с 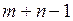базисными клетками.

Шаг 2. Определяем платежи 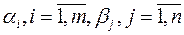из условий: 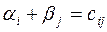для всех базисных клеток (ij). Один из платежей (в строке или в столбце которого максимальное число базисных клеток) полагаем равным нулю.

Шаг 3. Считаем псевдостоимости 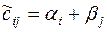для всех свободных клеток. Если 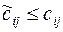для всех клеток, то план оптимален. Вычисляем значение целевой функции 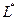на этом плане и исследование прекращаем.

Шаг 4. Если есть свободная клетка, для которой 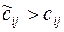, то улучшаем план, перебрасывая перевозки по циклу этой свободной клетки.

Шаг 5. Возвращаемся к шагу 2 для пересчета платежей нового опорного плана.

Пример решения транспортной задачи методом потенциалов

Решить методом потенциалов транспортную задачу:

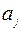	3	8	2
	7	4	8
				=

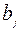Опорный план этой задачи найден методом северо-западного угла.

Приписываем к таблице строку для платежей 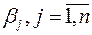и столбец для платежей 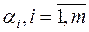. Псевдостоимости записываем в левом углу клетки, а стоимости – в правом.

Из условий 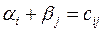в базисных клетках получаем систему уравнений:

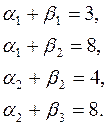
Полагая 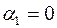, находим платежи 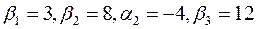и псевдостоимости для свободных клеток. Получаем таблицу

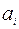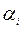	15 3	[-] 20 8	12[+] 2
	-1 7	[+] 0 4	[-] 30 8		-4
				=

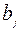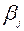Стоимость перевозок по плану этой таблицы:

.

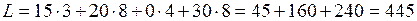Так как клетка (1,3) имеет отрицательную цену 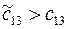, то план не является оптимальным. Строим для клетки (1,3) цикл. Цена цикла 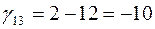. По циклу переносим 20 единиц груза (больше нельзя, чтобы перевозки в клетке (1,2) не стали отрицательными). При этом стоимость плана изменяется на 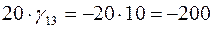. Для нового плана вычисляем новые значения платежей и псевдостоимостей:

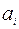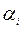	[-]15 3	-2 8	[+] 20 2
	9 [+] 7	20 4	[-] 10 8
				=
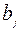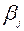		-2

Стоимость перевозок по плану этой таблицы:

.

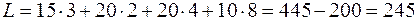Полученная таблица имеет клетку (2,1) с отрицательной ценой 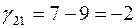. По циклу этой клетки переносим 10 единиц груза, при этом стоимость плана уменьшается на 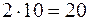единиц, и получаем новый опорный план с новой системой платежей и псевдостоимостей:

	5 3	0 8	30 2
	10 7	20 4	5 8
				=

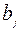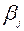Стоимость перевозок по плану этой таблицы:

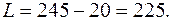
Так как в последней таблице все псевдостоимости не превосходят соответствующих стоимостей, то полученный опорный план 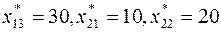является оптимальным. Стоимость перевозок при этом.

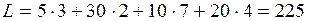
Библиографический список

1. Мину, М. Математическое программирование. Теория и алгоритмы / М. Мину. – М.: Наука, 1990.- 485 с.

2. Оуэн, Г. Теория игр / Г. Оуэн – М.: Мир, 1967.

3. Зайченко, Ю.П. Исследование операций / Ю.П. Зайченко. – Киев: Высш. шк., 1975.

4. Базара, М. Нелинейное программирование. Теория и алгоритмы. / М. Базара, К. Шетти – М.: Мир, 1982.- 583 с.

5. Зыкина, А.В. Задания для самостоятельной работы по курсу «Системный анализ и исследование операций»: метод. указ. /А.В. Зыкина – Омск: ОмГТУ, 1995.- 68 с.

6. Зыкина А.В. Теория игр и исследование операций: метод. указ. и контрольные задания для студентов заочного отделения экономического факультета

/ А.В. Зыкина, Л.А. Заозерская, В.П. Ильев – Омск: ОмГУ, 1999.- 48 с.

7. Теория принятия решений: Сб. заданий для практических занятий / А.В. Зыкина, О.Н. Канева – Омск: ОмГУ, 2006.- 56 с.

Оглавление

ВВЕДЕНИЕ……………………………………………………………………………... 3

1. ГРАФИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ ЛП……………………………..………….. 4

1.1. Каноническая форма задачи ЛП…………………………………………….....…4

1.2. Пример построения канонической формы………………………………….…...4

1.3. Общие рекомендации к графическому решению задач ЛП ………………..…. 5

1.4. Пример графического решения……………………………………………..……8

2. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЛП………………………………. 10

2.1. Симплекс-метод ……………………………………………………………...… 10

2.2. Алгоритм симплекс-метода для задачи на минимум………………………… 11

2.3. Алгоритм симплекс-метода для задачи на максимум …………………………12

2.4. Пример решения задачи симплекс-методом…………………………………...13

2.5. Метод искусственного базиса…………………………………………….……..14

2.6. Пример решения задачи методом искусственного базиса…………………….16

2.7. Двойственный симплекс-метод…………………………………………………19

2.8. Пример решения задачи двойственным симплекс-методом…………………..20

3. ДВОЙСТВЕННОСТЬ В ЛП…………………………………………………………21

3.1. Постановка задачи………………………………………………………………..21

3.2. Пример построения двойственной задачи……………………………………...22

3.3. Теоремы двойственности………………………………………………………...22

3.4. Пример решения пары двойственных задач……………………………………23

3.5. Пример проверки вектора на оптимальность…………………………………..24

4. МЕТОД ГОМОРИ……………………………………………………………………25

4.1. Постановка задачи ЦЛП…………………………………………………………25

4.2. Алгоритм метода Гомори………………………………………………………..26

4.3. Пример решения задачи ЦЛП…………………………………………………...27

5. ТРАНСПОРТНАЯ ЗАДАЧА ЛП…………………………………………………….28

5.1. Постановка задачи………………………………………………………………..28

5.2. Построение опорного плана транспортной задачи…………………………….29

5.3. Метод северо-западного угла……………………………………………………30

5.4. Пример построения опорного плана методом северо-западного угла………..31

5.5. Метод минимальной стоимости…………………………………………………31

5.6. Пример построения опорного плана методом минимальной стоимости…….31

5.7. Метод потенциалов………………………………………………………………32

5.8. Вычислительная схема метода потенциалов…………………………………...32

5.9. Пример решения транспортной задачи методом потенциалов………………..33

БИБЛИОГРАФИЧЕСКИЙ СПИСОК…………………………………………………..35