Линейные и разветвляющиеся алгоритмы
ЗАДАНИЯ ПО КУРСУ
«ПРОГРАММИРОВАНИЕ»
ВАРИАНТ B
МИНСК
ОГЛАВЛЕНИЕ
1 семестр. 4
1. Линейные и разветвляющиеся алгоритмы.. 5
1.1. Вычисления по формулам. Стандартные математические функции. 5
1.2. Область на плоскости. 6
1.3. Условный оператор. 8
1.4. Логическое выражение в условном операторе. 9
1.5. Ветвления. 10
1.6. Побитовые операции. 12
2. Циклы.. 13
2.1. Целочисленная арифметика. приведение типов. 13
2.2. Итерационные циклы.. 15
2.3. Нахождение простых чисел. 17
2.4. Вычисления с точностью.. 18
2.5. Последовательности значений. 19
2.6. Вычисления без хранения последовательности значений. 20
2.7. Схема Горнера. 21
3. Массивы. Указатели. 22
3.1. Обработка одномерных массивов. 22
3.2. Построение новой матрицы по части заданной матрицы.. 23
3.3. Обход матрицы.. 24
3.4. Алгоритм Эратосфена для нахождения простых чисел. 25
3.5. Упорядоченность значений в матрицах. 25
3.6. Преобразование матриц. 26
3.7. Использование массивов для представления «длинных» чисел. 28
3.8. Экономичное хранение матриц. Матричная алгебра. 29
4. Строки. 30
4.1. Использование строкового типа. 30
4.2. Перевод из одной cистемы счисления в другую.. 31
4.3. Выделение слов в строке. 32
4.4. Массив слов. 33
2 семестр. 34
5. Функции. 35
5.1. Передача массивов в функцию.. 35
5.2 Создание собственных процедур для обработки С-строк. 36
5.3. Возврат ссылок. 37
5.4. Рекурсия. 39
5.5. Вычисление корня уравнения. Передача имени функции в качестве параметра. Аргументы по умолчанию.. 40
5.6. Вычисление интеграла. Передача имени функции в качестве параметра. 42
5.7. Сортировка массивов. 44
5.8. Сортировка слиянием.. 44
5.9. Перебор с возвратом.. 45
6. Файлы.. 46
6.1. Файлы чисел. 46
6.2. Файлы записей. 47
6.3. Использование структур для битового представления чисел. 48
7. Динамические структуры данных. 49
7.1. Динамическое выделение памяти для массивов. 49
7.2. Линейный список. 51
7.3. Линейные списки. 52
7.4. Двухсвязные списки. 53
7.5. Деревья. 54
7.6. Графы.. 55
7.7. Более сложные связанные динамические структуры данных. 56
8. Классы.. 57
8.1. Класс «Многоразрядное число». 57
8.2. Перегрузка операций. 59
8.3 Класс «Матрица». 61
8.4 Класс «Линейный список». 62
8.5. Класс «Двусвязный список». 62
8.6. Класс «Бинарное дерево». 63
8.7. Класс «Граф». 64
8.8. Библиотека шаблонов STL. Векторы.. 65
8.9. Библиотека шаблонов STL . Списки. 65
8.10. Библиотека шаблонов STL . Ассоциативные Списки. 65
9. Наследование. Полиморфизм.. 66
9.1. Наследование. 66
9.2. Полиморфизм. Виртуальные методы.. 67
9.3. Полиморфизм. Виртуальные методы.. 68
Семестр
Занятий
| Оценка | количество задач |
| № | тема | № задач | |||
| 1. Линейные алгоритмы | 1.1 1.2 | ||||
| 1.3 | 1.5 | ||||
| 1.4 | 1.6 | ||||
| 2. Циклы | 2.1 | ||||
| 2.2 | 2.5 | ||||
| 2.3 | 2.6 | ||||
| 2.4 | 2.7 | ||||
| 3. Массивы. Указатели | 3.1 | 3.4 | |||
| 3.2 | 3.6 | ||||
| 3.3 | 3.7 | ||||
| 3.5 | 3.8 | ||||
| 4.Строки | 4.1 | ||||
| 4.2 | |||||
| 4.3 | 4.4 | ||||
| Зачет |
Линейные и разветвляющиеся алгоритмы
Вычисления по формулам. Стандартные математические функции
Найти область допустимых значений функции и написать программу, вычисляющую значение функции для заданных начальных данных (s, t - целые, x - вещественное), обеспечив варианты: ввода данных с клавиатуры, инициализации данных в программе, вывода результата на экран.
Для тестирования исходные данные задавать как целые, вещественные с фиксированной точкой, плавающей точкой.
1. 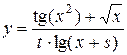 ; 2.
; 2. 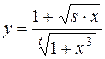 ;
;
3. 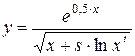 ; 4.
; 4. 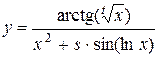 ;
;
5. 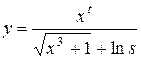 ; 6.
; 6. 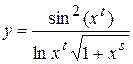 ;
;
7. 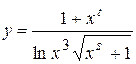 ; 8.
; 8. 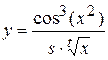 ;
;
9. 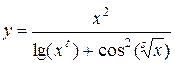 ; 10.
; 10. 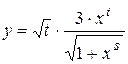 ;
;
11. 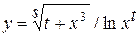 ; 12.
; 12. 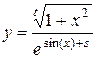 .
.
Область на плоскости
Даны вещественные числа x, y. Определить, принадлежит ли точка с координатами x, y заштрихованной части плоскости, включая границы. Числа R, x, y вводятся с клавиатуры.
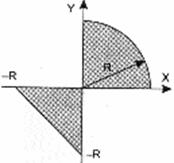 |
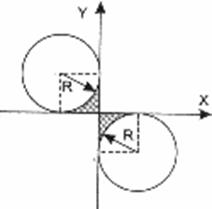 |
1. 2.
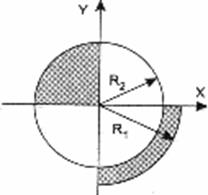 | 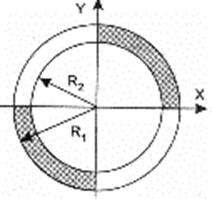 | ||
3. 4.
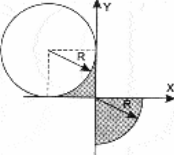 | 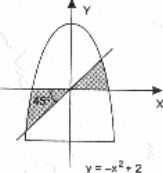 | ||
5. 6.
7. 8.
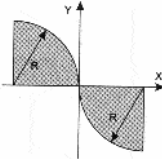 | 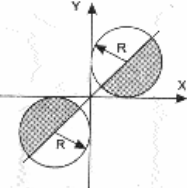 | ||
9. 10.
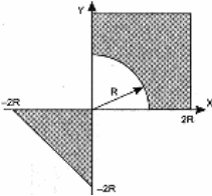
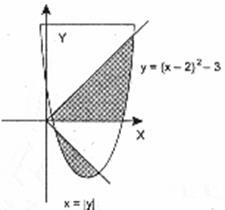
11. 12.
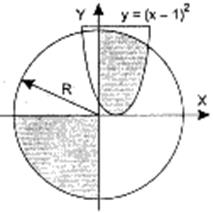
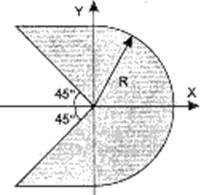
Условный оператор
Выполнить задания двумя способами: с использованием оператора if и с использованием условного оператора ?. Выполнить задания, минимизируя количество выполняемых операций сравнения и присваивания.
1.Даны действительные числа x, y, z. Поменять значения переменных так, чтобы x ³ y ³ z;
2.Даны действительные числа x, y, z. Поменять значения переменных так, чтобы x < y < z;
3.Даны вещественные x1, x2, x3, x4 . Поменять значения переменных так, чтобы x1< x2 < x3< x4 .
4.Даны вещественные x1, x2, x3, x4 . Поменять значения переменных так, чтобы x1 > x2 > x3 > x4 .
5.Даны вещественные x1, x2, x3, x4 .Поменять значения переменных так, чтобы x1³ x2 < x3 ³ x4 .
6.Даны вещественные x1, x2, x3, x4 . Поменять значения переменных так, чтобы x1 < x2 > x3 < x4 .
7.Даны действительные числа x1, x2, x3, x4. Поменять значения переменных так, чтобы x1 ³ x2 ³ x3 ³ x4;
8.Даны действительные числа x1, x2, x3, x4. Поменять значения переменных так, чтобы x1 < x2 > x3 > x4.
9.Даны вещественные x1, x2, x3, x4 . Поменять значения переменных так, чтобы x1 > x2 > x3< x4 .
10.Даны вещественные x1, x2, x3, x4 . Поменять значения переменных так, чтобы x1 < x2 > x3 > x4 .
11.Даны вещественные x1, x2, x3, x4 . Поменять значения переменных так, чтобы x1³ x2 < x3 ³ x4 .
12.Даны вещественные x1, x2, x3, x4 . Поменять значения переменных так, чтобы x1 < x2 > x3 < x4 .
Ветвления
Выполнить задания двумя способами: с использованием оператора if и с использованием условного оператора ?.
1. Даны вещественные числа a1, b1, c1, a2, b2, c2. Найти все решения системы линейных алгебраических уравнений:
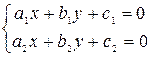
2. Даны вещественные числа a1, b1, c1, a2, b2, c2. Найти координаты точки пересечения двух прямых, описываемых уравнениями a1x + b1y = c1 и a2x + b2y = c2 , либо сообщить: прямые совпадают, не пересекаются, не существуют.
3. Даны a, b, c, d, e, f, g, h – вещественные числа. Точки (a, b), (c, d) не лежат на прямой l, проходящей через точки (e, f), (g, h). Прямая l разбивает плоскость на две полуплоскости. Определить, принадлежат ли заданные точки (a, b), (c, d) разным полуплоскостям.
4. Даны a, b, c – вещественные числа. Исследовать биквадратное уравнение ax4+ bx2 + c = 0, т.е. определить все действительные корни данного уравнения, если они есть.
5. Даны a, b, c, d, e, f, s, t, u – вещественные числа. Точки (a, b), (c, d), (e, f) не лежат на прямой l, заданной уравнением sx + ty + u = 0. Прямая l разбивает плоскость на две полуплоскости. Определить, принадлежит ли треугольник с вершинами (a, b), (c, d), (e, f) одной полуплоскости.
6. Даны x1, x2, x3, y1, y2, y3– вещественные числа. Определить, принадлежит ли треугольнику с вершинами (x1, y1), (x2, y2), (x3, y3) начало координат, т. е. точка с координатами (0, 0).
7. Даны x1, x2, x3, y1, y2, y3, x, y – вещественные числа. Определить, принадлежит ли треугольнику с вершинами (x1, y1), (x2, y2), (x3, y3) точка с координатами (x, y).
8. Даны a, b, c, d, e, f, s, t, u – вещественные числа. Точки (a, b), (c, d), (e, f) не лежат на прямой l, заданной уравнением sx + ty + u = 0. Прямая l разбивает плоскость на две полуплоскости. Определить, принадлежит ли треугольник с вершинами (a, b), (c, d), (e, f) одной полуплоскости.
9. Даны x1, x2, …x6, y1, y2, … y6– вещественные числа. Точки с координатами (x1, y1), (x2, y2), (x3, y3) рассматриваются как три вершины первого прямоугольника, точки с координатами (x4, y4), (x5, y5), (x6, y6) – второго. Выяснить, лежит ли какой-либо из прямоугольников целиком внутри другого.
10. Даны x1, x2, …x6, y1, y2, … y6– вещественные числа. Точки с координатами (x1, y1), (x2, y2), (x3, y3) рассматриваются как три вершины первого прямоугольника, точки с координатами (x4, y4), (x5, y5), (x6, y6) – второго. Выяснить, верно ли, что первый прямоугольник целиком содержится во втором.
11. Даны x1, x2, …x6, y1, y2, … y6– вещественные числа. Точки с координатами (x1, y1), (x2, y2), (x3, y3) рассматриваются как вершины первого треугольника, точки с координатами (x4, y4), (x5, y5), (x6, y6) – второго треугольника. Выяснить, верно ли, что первый треугольник целиком содержится во втором.
12. Даны x1, x2, …x6, y1, y2, … y6– вещественные числа. Точки с координатами (x1, y1), (x2, y2), (x3, y3) рассматриваются как вершины первого треугольника, точки с координатами (x4, y4), (x5, y5), (x6, y6) – второго треугольника. Выяснить, лежит ли какой-либо из треугольников целиком внутри другого.
1.6. Побитовые операции
1.Задано число n в формате char. Вывести на экран значения 0-ого и 7-ого битов представления в ЭВМ этого значения. Объяснить результат. Инвертировать биты 1,3. Вывести и объяснить результат.
2.Задано число n в формате unsigned char. Вывести на экран значения 0-ого и 7-ого битов представления в ЭВМ этого числа. Объяснить результат. Инвертировать биты 2,4. Вывести и объяснить результат.
3.Задано число n в формате signed char. Вывести на экран значения 0-го, 3-го и 7-го битов представления в ЭВМ этого числа. Объяснить результат. Инвертировать биты 3,6. Вывести и объяснить результат.
4.Задано число n в формате short int. Вывести на экран значения 0-ого, 3-ого и 13-ого битов представления в ЭВМ этого числа. Объяснить результат. Инвертировать биты 1,7. Вывести и объяснить результат.
5.Задано число n в формате unsigned short int. Вывести на экран значения 0-го, 7-го и 15-го битов представления в ЭВМ этого числа. Объяснить результат. Инвертировать биты 7,8. Вывести и объяснить результат.
6.Задано число n в формате signed short int. Вывести на экран значения 0-го, 2-го и 15-го битов представления в ЭВМ этого числа. Объяснить результат. Инвертировать биты 1,15. Вывести и объяснить результат.
7.Задано число n в формате int. Вывести на экран значения 0-го, 1-го и 15-го битов представления в ЭВМ этого числа. Объяснить результат. Инвертировать биты 7,15. Вывести и объяснить результат.
8.Задано число n в формате unsigned int. Вывести на экран значения 0-ого и 15-ого битов представления в ЭВМ этого числа. Объяснить результат. Инвертировать биты 7,15. Вывести и объяснить результат.
9.Задано число n в формате signed int. Вывести на экран значения 0-го, 3-го и 15-го битов представления в ЭВМ этого числа. Объяснить результат. Инвертировать биты 1,7. Вывести и объяснить результат.
10.Задано число n в формате unsigned long. Вывести на экран значения 0-го, 1-го и 15-го битов представления в ЭВМ этого числа. Объяснить результат. Инвертировать биты 1,10. Вывести и объяснить результат.
11.Задано число n в формате signed long. Вывести на экран значения 0-го, 1-го и 7-го битов представления в ЭВМ этой переменной. Объяснить результат. Инвертировать биты 0,1. Вывести и объяснить результат.
12.Задано число n формате long. Вывести на экран значения 0-го, 1-го и 7-го битов представления в ЭВМ этой переменной. Объяснить результат. Инвертировать биты 1,15. Вывести и объяснить результат.
Циклы
2.1.Целочисленная арифметика. приведение типов
2.1.1. Выполнить задания, выделяя цифры числа, хранящегося в переменной стандартного целого типа. Число n вводится с клавиатуры.
1.Дано натуральное n. Верно ли, что это число содержит только две одинаковых цифры?
2.Дано натуральное n. Верно ли, что это число содержит ровно три одинаковых цифры?
3.Дано натуральное n. Определить, является ли это число палиндромом.
4.Дано натуральное n. Верно ли, что все цифры числа различны?
5.Дано натуральное n. Верно ли, что это число содержит ровно k одинаковых цифр?
6.Дано натуральное n. Верно ли, что все цифры числа различны?
7.Дано натуральное n. Верно ли, что это число содержит ровно 2 одинаковых цифры?
8.Дано натуральное n. Верно ли, что это число содержит более k одинаковых цифр?
9.Определить, равна ли сумма k первых цифр заданного натурального числа, сумме k его последних цифр.
10.Дано натуральное n. Верно ли, что это число содержит более k одинаковых цифр?
11.Дано натуральное n. Верно ли, что это число содержит k цифр, значения которых меньше заданного m?
12.Дано натуральное n. Верно ли, что это число содержит более k цифр больших суммы первых 2 цифр.
2.1.2. Выполнить задания, выделяя цифры числа, хранящегося в переменной стандартного вещественного типа. Число n вводится с клавиатуры.
1.Определить, сколько среди первых k цифр дробной части заданного положительного вещественного числа, цифр 9.
2.Определить сумму первых k цифр дробной части заданного положительного вещественного числа.
3.Определить, равна ли сумма первых k цифр дробной части заданного положительного вещественного числа сумме n следующих цифр.
4.Определить, равна ли k-ая цифра дробной части заданного положительного вещественного числа сумме n следующихцифр.
5.Определить, равна ли k-ая цифра дробной части заданного положительного вещественного числа сумме n предыдущихцифр.
6.Определить сумму k цифр дробной части заданного положительного вещественного числа, которые следуют за n-ойцифрой.
7.Определить равна ли сумма k цифр дробной части заданного положительного вещественного числа сумме цифр целой части этого числа.
8.Верно ли, что первые n цифр дробной части заданного положительного вещественного числа образуют возрастающую последовательность?
9.Верно ли, что первые n цифр дробной части заданного положительного вещественного числа различны?
10.Верно ли, что первые n цифр дробной части заданного положительного вещественного числа одинаковы?
11.Верно ли, что первые n цифр дробной части заданного положительного вещественного числа образуют монотонную последовательность?
12.Верно ли, что первые n цифр дробной части заданного положительного вещественного числа образуют арифметическую прогрессию?
Итерационные циклы
Составить программу вычисления значений функции в точках хi Î [х0; хn], хi = х0 + iDх, i = 0,1, …, воспользовавшись формулами разложения элементарных функций в ряд Тейлора с точностью e = 10–6. Вывести на экран необходимое количество слагаемых в каждом случае. Сравнить результаты со значениями функции в этих точках, вычисленных с помощью встроенных функций системы программирования.
1. 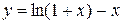 ; х0 = – 0,8; хn = 1; Dх = 0,1;
; х0 = – 0,8; хn = 1; Dх = 0,1;
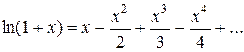 .
.
2. 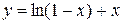 ; х0 = – 0,8; хn = 1; Dх = 0,1;
; х0 = – 0,8; хn = 1; Dх = 0,1;
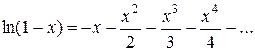 .
.
3. 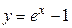 ; х0 = – 4; хn = 6; Dх = 0,5;
; х0 = – 4; хn = 6; Dх = 0,5;
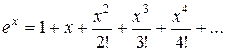 .
.
4. 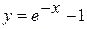 ; х0 = – 2; хn = 2; Dх = 0,2
; х0 = – 2; хn = 2; Dх = 0,2
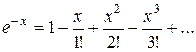 .
.
5. 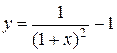 ; х0 = – 0,4; хn = 0,6; Dх = 0,1
; х0 = – 0,4; хn = 0,6; Dх = 0,1
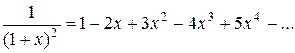 .
.
6. 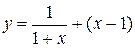 ; х0 = – 0,5; хn = 0,5; Dх = 0,1;
; х0 = – 0,5; хn = 0,5; Dх = 0,1;
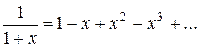 .
.
7. 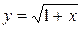 ; х0 = – 0,5; хn = 0,5; Dх = 0,1;
; х0 = – 0,5; хn = 0,5; Dх = 0,1;
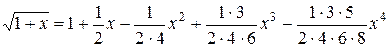 +… .
+… .
8. 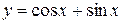 ; х0 = 0; хn = 2p; Dх = 0,1;
; х0 = 0; хn = 2p; Dх = 0,1;
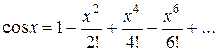
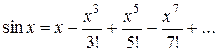 .
.
9. 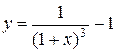 ; х0 = – 0,6; хn = 0,8; Dх = 0,1;
; х0 = – 0,6; хn = 0,8; Dх = 0,1;
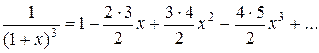 .
.
10. 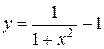 ; х0 = – 0,1; хn = 0,9; Dх = 0,2;
; х0 = – 0,1; хn = 0,9; Dх = 0,2;
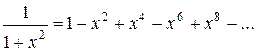 .
.
11. 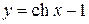 ; х0 = –3; хn = 4; Dх = 1;
; х0 = –3; хn = 4; Dх = 1;
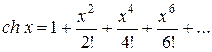 .
.
12. 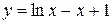 ; х0 = 0; хn = 1; Dх = 0,1;
; х0 = 0; хn = 1; Dх = 0,1;
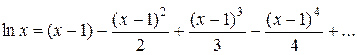 .
.
Нахождение простых чисел
1.Дано натуральное n. Получить все его простые делители.
2.Сверхпростым называется число, если оно простое, и число, полученное из исходного числа при записи цифр исходного числа в обратном порядке («перевертыш»), тоже будет простым. Написать программу, которая выводит все сверхпростые числа в диапазоне от а до b.
3.Дано натуральное число n. Получить его каноническое разложение (разложение на простые множители).
4.Дано натуральное число n. Среди чисел n, n + 1, …, 2n найти все числа-близнецы: простые числа, разность между которыми равна 2.
5.Дано натуральное число n. Найти четверки меньших n простых чисел, принадлежащих одному десятку.
6.Сверхпростое число — это простое число, номер которого в списке простых чисел, упорядоченном по возрастанию, является простым числом. Найдите k-ое сверхпростое число.
7.Найти n первых простых чисел, сумма цифр у которых меньше заданного m.
8.Среди всех четырехзначных чисел получить все простые числа, у каждого из которых сумма первых двух цифр равна сумме двух последних цифр.
9.Натуральное число, записанное в десятичной системе счисления, называется сверхпростым, если оно остается простым при любой перестановке своих цифр. Найти все трехзначные сверхпростые числа.
10.Сверхпростым называется число, если оно простое, и число, полученное из исходного числа при записи цифр исходного числа в обратном порядке («перевертыш»), тоже будет простым. Найти все четырехзначные сверхпростые числа.
11.Найти натуральные числа из диапазона от n до k, количество делителей у которых – произведение двух простых чисел.
12.Дано n – натуральное число. Среди простых чисел £ n,найти такое, в двоичной записи которого максимальное количество единиц.
Вычисления с точностью
Дано действительное число х (0 < x £ 1). Вычислить заданную сумму с точностью e = 10–6 и указать количество слагаемых. Считать, что требуемая точность достигнута, если очередное слагаемое по абсолютному значению меньше e:
1. 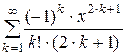 ; 2.
; 2. 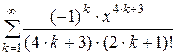 ;
;
3. 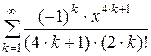 ; 4.
; 4. 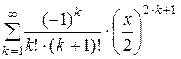 ;
;
5. 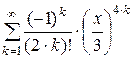 ; 6.
; 6. 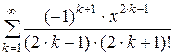 ;
;
7. 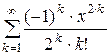 ; 8.
; 8. 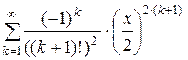 ;
;
9. 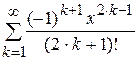 ; 10.
; 10. 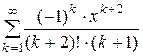 ;
;
11. 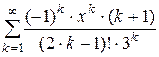 ; 12.
; 12. 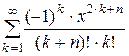 .
.
Последовательности значений
Выполнить задания без хранения последовательности значений.
1.Вводится последовательность целых чисел. Определить количество элементов в наиболее длинной подпоследовательности подряд идущих чисел, упорядоченных по убыванию.
2.Вводится последовательность целых чисел. Определить количество элементов в наиболее длинной подпоследовательности подряд идущих чисел, упорядоченных по возрастанию.
3.Вводится последовательность целых чисел. Определить количество элементов в наиболее длинной подпоследовательности подряд идущих чисел, образующих арифметическую прогрессию.
4.Вводится последовательность целых чисел. Определить количество элементов в наиболее длинной подпоследовательности подряд идущих чисел, представляющих собой полные квадраты.
5.Вводится последовательность целых чисел. Определить количество элементов в наиболее длинной подпоследовательности подряд идущих чисел, представляющих собой числа Фиббоначи.
6.Вводится последовательность целых чисел. Определить количество элементов в наиболее длинной подпоследовательности подряд идущих чисел, представляющих собой степени двойки.
7.Вводится последовательность из n целых чисел. Определить количество элементов в наиболее длинной подпоследовательности подряд идущих чисел, представляющих собой геометрическую прогрессию.
8.Вводится последовательность из n целых чисел. Определить количество элементов в наиболее длинной подпоследовательности подряд идущих чисел одного знака.
9.Вводится последовательность из n целых чисел. Определить количество элементов в наиболее длинной подпоследовательности подряд идущих нулей.
10.Вводится последовательность из n вещественных чисел. Определить количество элементов в наиболее длинной подпоследовательности подряд идущих чисел, представляющих собой степени тройки.
11.Вводится последовательность из n целых чисел. Определить количество элементов в наиболее длинной подпоследовательности подряд идущих чисел, представляющих собой степени пятерки.
12.Дана непустая последовательность X ненулевых целых чисел, за которой следует 0. Вычислить величину: 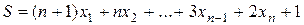 .
.
Схема Горнера
Вычислить значение многочлена для заданного n в точках хi Î [х0; хm] (хi = х0 + iDх, i = 0,1,…,) двумя способами: суммируя элементы по возрастанию степени x и по схеме Горнера. Посчитать количество операций сложения и умножения в том и другом случае.
1. 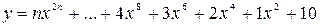
х0 = 1, хm =2, Dх = 0,25.
2. 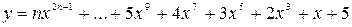
х0 = 1, хm =5, Dх = 0,5.
3. 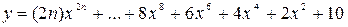
х0 = 1, хm =2, Dх = 0,25.
4. 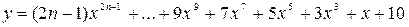
х0 = 1, хm =5, Dх = 0,5.
5. 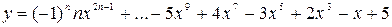
х0 = 1, хm =5, Dх = 0,5.
6. 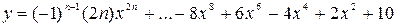
х0 = 1, хm =2, Dх = 0,25.
7. 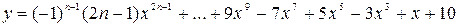
х0 = 1, хm =5, Dх = 0,5.
8. 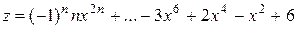
х0 = 1, хm = 3, Dх = 0,2
9. 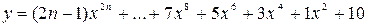
х0 = 1, хm =2, Dх = 0,25.
10. 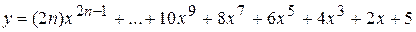
х0 = 1, хm =5, Dх = 0,5.
11. 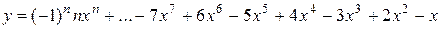
х0 = 0, хm = 4, Dх = 0,4
12. 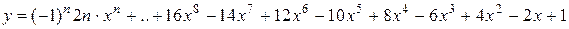
х0 = 0, хm = 4, Dх = 0,4
Массивы. Указатели
1. 2. 3. 4.
 |
5. 6. 7. 8.
9. По матрице A построить матрицу B того же размера, где элемент bij определяется следующим образом. Через aij проведем в A линии, параллельные сторонам прямоугольника до пересечения с главной диагональю; bij определяется как минимум среди элементов треугольника в А.
10. По матрице A построить матрицу B того же размера, где элемент bij определяется следующим образом. Через aij проведем в A линии, параллельные сторонам прямоугольника до пересечения с побочной диагональю; bij определяется как максимум среди элементов треугольника в А.
11. По матрице А построить матрицу В того же размера, где bij определяется следующим образом. Через aij проведем в A диагонали, параллельные главной и побочной диагоналям; bij определяется как максимум в закрашенной части матрицы А.
12. По матрице А построить матрицу В того же размера, где bij определяется следующим образом. Через aij проведем в A диагонали, параллельные главной и побочной диагоналям; bij определяется как максимум в закрашенной части матрицы А.
 |
9. 10. 11. 12.
3.3.Обход матрицы
Получить квадратную матрицу порядка n, элементами которой являются заданные действительные числа а1, ..., аnn, расположенные в ней по схеме, которая приведена на рисунке.
 |
1. 2. 3. 4.
 |
5. 6. 7. 8.
Вывести последовательность действительных чисел b1, ..., bnn, получающуюся при чтении заданной квадратной матрицы порядка n по спирали.

9. 10. 11. 12.
Строки.
4.1. Использование строкового типа
Выполнить задание двумя способами, используя C-строки для представления данных и используя string-строки.
1.Если заданный текст является правильной записью римскими цифрами целого числа от 1 до 1999, то получить это число.
2.Заданное натуральное число от 1 до 1999 вывести римскими цифрами.
3.Из заданного текста удалить те символы, которые встречаются в нем ровно один раз.
4.Из заданного текста удалить символы, которые встречаются в нем более одного раза.
5.Из заданного текста удалить те символы, которые встречаются в нем ровно два раза.
6.Из заданного текста удалить те символы, которые встречаются в нем более двух раз.
7.Из заданного текста удалить символы, которые образуют максимальную серию.
8.Для каждого символа заданного текста указать, сколько раз он встречается в тексте. Удалить символы, которые встречаются более одного раза.
9.Исключить из строки группы символов, расположенные между символами '(' и ')' вместе со скобками. Если нет символа ')' для ‘(‘, то исключить все символы до конца строки после '(.
10.Определить является ли введенный текст: идентификатором, записью целого числа.
11.Определить является ли введенный текст записью вещественного числа (с фиксированной точкой, с плавающей точкой).
12.Задан текст, в котором нет символов '(' и ')'. Выполнить его сжатие, т. е. заменить всякую максимальную подпоследовательность, составленную из более чем трех вхождений одного и того же символа, на (k)s, где s – повторяемый символ, a k > 3 – количество его повторений.
Выделение слов в строке
Выполнить следующие задания для заданной строки символов (заданного текста)двумя способами, используя C-строки для представления данных и используя string-строки.
Текст– непустая последовательность символов.
Слово – непустая последовательность любых символов, кроме символов-разделителей.
Предложение – последовательность слов, разделенных одним или несколькими символами-разделителями.
Символы-разделители: «пробел», «.», «,», «:», «;», «!», «?», «-», «(», «)».
1.Записать в новую строку слова, которые состоят из тех же букв, что и первое слово в заданной строке символов.
2.Записать в новую строку слова, которые состоят из тех же букв, что и последнее слово заданной строки символов.
3.Записать в новую строку все несимметричные слова, которые имеют четную длину.
4.Записать в новую строку слова, которые имеют такую же длину, что и последнее слово заданной строки символов.
5.Записать в новую строку слова исходной строки, в которых количество гласных букв максимально.
6.Записать в новую строку слова исходной строки, в которых количество согласных букв максимально.
7.Записать в новую строку слова исходной строки, в которых нет повторяющихся букв
8.Записать в новую строку слова исходной строки, в которых повторяющихся букв больше неповторяющихся.
9.Записать в новую строку слова исходной строки, в которых буквы упорядочены по алфавиту.
10.Записать в новую строку слова исходной строки, в которых нет одинаковых символов.
11.Записать в новую строку слова исходной строки, в которых каждый символ слова повторяется.
12.Заменить всякое вхождение слова вида аbc на b, где a, b – подслова, c – обращение слова a.
Массив слов
Выполнить следующие задания для заданной строки символов (заданного текста)двумя способами, используя C-строки для представления данных и используя string-строки.
1.В заданном тексте найти все пары слов, в которых одно является обращением другого.
2.В заданном тексте найти все слова, которые состоят из одинаковых наборов символов (количество повторений символов не учитывать).
3.В заданном тексте найти все слова, которые имеют одинаковую длину и состоят из одинаковых наборов символов (порядок символов может быть различный).
4.Для каждого слова заданного предложения указать, сколько раз оно встречается в предложении.
5.Вывести слово, наиболее часто встречающееся в строке.
6.Получить текст, в котором слова исходного текста упорядочены по длине слов.
7.Получить текст, в котором слова исходного текста упорядочены по алфавиту.
8.Получить текст, в котором слова исходного текста упорядочены по первой букве каждого слова.
9.Отредактировать заданное предложение, удаляя из него слова-се
