Вычисление значения многочлена

Вычислить значение многочлена для заданного n в точках х_i Î [х₀; х_m] (х_i = х₀ + iDх, i = 0,1,…) суммируя элементы по возрастанию степени x.

1.

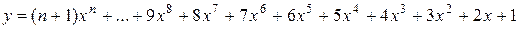
х₀ = 2, х_m =4, Dх = 0,2.

2.

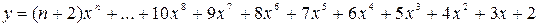
х₀ = 1, х_m =5, Dх = 0,5.

3.

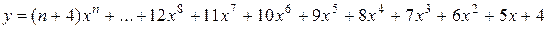
х₀ = 0, х_m =3, Dх = 0,25.

4.

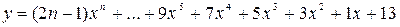
х₀ = 2, х_m =4, Dх = 0,2.

5.

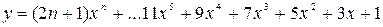
х₀ = 2, х_m =4, Dх = 0,25.

6.

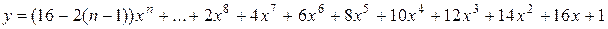
х₀ = 0, х_m =3, Dх = 0,25.

7.

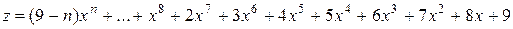
х₀ = 1, х_m =2, Dх = 0,2.

8.

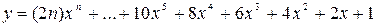
х₀ = 1, х_m =5, Dх = 0,5.

9.

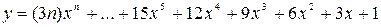
х₀ = 1, х_m =4, Dх = 0,5.

10.

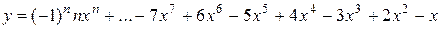
х₀ = 0, х_m = 3, Dх = 0,5

11.

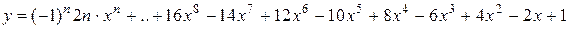
х₀ = 2, х_m =4, Dх = 0,2.

12.

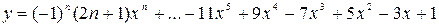
х₀ = 2, х_m =4, Dх = 0,2.

Перебор значений

1. Определить количество трехзначных натуральных чисел, сумма цифр которых равна n.

2. Ввести с клавиатуры натуральное число n. Определить все способы выплаты суммы n с помощью купюр достоинством 1, 5, 10, 20 и 100 условных единиц.

3. Ввести с клавиатуры целое число n. Определить все способы выплаты суммы n с помощью монет достоинством в 1, 5, 10, 15, 20, 50 копеек.

4. Два двузначных числа, записанных подряд, образуют четырехзначное число, которое нацело делится на их произведение. Найти все такие числа.

5. Вывести на экран в возрастающем порядке все трехзначные числа, в десятичной записи которых нет одинаковых цифр.

6. Даны натуральные числа m, n. Получить все натуральные числа меньшие n, квадрат суммы цифр которых равен m.

7. Найти все натуральные числа, не превосходящие заданного числа N и неделящиеся нацело не на одну из своих цифр.

8. Найти все пары двухзначных натуральных чисел М, N таких, что значение произведения М × N не изменится, если поменять местами цифры каждого из сомножителей.

9. Найти все натуральные числа, не превосходящие заданного числа N, десятичная запись которых есть строго возрастающая последовательность цифр.

10. Найти все натуральные числа, не превосходящие заданного числа N, десятичная запись которых есть строго убывающая последовательность цифр.

11. Построить таблицу всех различных разбиений заданного натурального числа N на сумму трех натуральных слагаемых (разбиения, отличающиеся порядком слагаемых, различными не считаются).

12. Найти все натуральные числа, не превосходящие заданного числа N и делящиеся нацело на каждую из своих цифр.

Простые числа

1. Найти все простые числа, не превосходящие заданного натурального числа n.

2. Дано натуральное n. Получить все его простые делители.

3. Среди всех четырехзначных чисел получить все простые числа, у каждого из которых сумма первых двух цифр равна сумме двух последних цифр.

4. Дана последовательность натуральных чисел длины n. Вычислить сумму тех из них, порядковые номера которых – простые числа.

5. Дана последовательность натуральных чисел длины n. Вычислить сумму тех из них, которые – простые числа.

6. Получить 100 первых простых чисел.

7. Получить m первых простых чисел.

8. Дано натуральное число n. Среди чисел n, n + 1, …, 2n найти все числа-близнецы: простые числа, разность между которыми равна 2.

9. Найти все простые числа, не превосходящие заданного натурального числа n, сумма цифр которых меньше m.

10. Определить количество простых чисел, попадающих в диапазон допустимых значений типа unsigned short int.

11. Определить количество простых чисел, попадающих в диапазон допустимых значений типа unsigned int.

12. Натуральное число, записанное в десятичной системе счисления, называется сверхпростым, если оно остается простым при любой перестановке своих цифр. Найти двузначные сверхпростые числа.

Условные циклы

1. Определить, какую наибольшую степень числа 100 можно вычислить, пользуясь типом int.

2. Определить, какую наибольшую степень числа 3 можно вычислить, пользуясь типом short int.

3. Определить, для какого наибольшего n можно вычислить значение n!, пользуясь типом int.

4. Определите номер максимального элемента последовательности Фиббоначчи, попадающего в диапазон допустимых значений типа unsigned char.

5. Определить, для какого наибольшего n можно вычислить значение (2n)!! (произведение всех четных натуральных чисел, не превышающих 2n), пользуясь типом int.

6. Определить, для какого наибольшего n можно вычислить значение (2n+1)!! (произведение всех нечетных натуральных чисел, не превышающих 2n+1), пользуясь типом unsigned int.

7. Определить, какую наибольшую степень числа 7 можно вычислить, пользуясь типом signed short.

8. Определить, какую наибольшую степень числа 10 можно вычислить, пользуясь типом Longint.

9. Определить, для какого наибольшего n можно вычислить значение n!, пользуясь типом unsigned long.

10. Определите номер максимального элемента последовательности Фиббоначчи, попадающего в диапазон допустимых значений типа unsigned char.

11. Определить, для какого наибольшего n можно вычислить значение (2n)!! (произведение всех четных натуральных чисел, не превышающих 2n), пользуясь типом long.

12. Определить, для какого наибольшего n можно вычислить значение (2n+1)!! (произведение всех нечетных натуральных чисел, не превышающих 2n+1), пользуясь типом unsigned int.

Пошаговый ввод данных

Выполнить задание без хранения последовательности значений..

1. Вводятся натуральное число n, целые числа а₁, ..., a_n. Вычислить сумму: а₁ + а₂ ²+ ... + a_nⁿ.

2. Вводятся натуральное число n, целые числа x₁, x₂, ..., x_n. Вычислить:

.

3. Заданы натуральные числа m, n. Вводятся целые числа а₁, ..., a_n.

Вычислить b₁ + ... + b_m, где

b₁ = а₁ + а₂ + ... + a_n; b₂ = а₁² + а₂²+ ... + a_n²; ... b_m= а₁ ^m + а₂ ^m + ... + a_n^m .

4. Заданы натуральные числа m, n, вводятся действительные числа а₁, ..., a_nm. Вычислить: .

5. Вводится последовательность из n ненулевых целых чисел. Определить, сколько раз в этой последовательности меняется знак чисел.

6. Вводится последовательность из n вещественных чисел. Найти порядковый номер того из них, которое наиболее близко к какому-либо целому.

7. Вводится последовательность из n вещественных чисел. Определить, сколько из них больше своих соседей, т. е. предыдущего и последующего.

8. Вводится n целых чисел x₁, x₂, ..., x_n. Вычислить величину:

.

9. Вычислить для заданных n и целых числах с₁, с₂, ..., с_n и s₁, s₂, ..., s_n:

.

10. Вычислить для заданных значений натурального n, действительных а₁, а₂, ..., а_n: .

11. Вычислить для заданных значений натурального n, действительных а₁, а₂, ..., а_n: .

12. Вычислить для заданных значений натурального n, действительных а1, а2, ..., аn:

.

Массивы

Одномерный массив

Для тестирования предусмотреть возможность задавать элементы массива различным образом: при описании с инициализацией, присвоением значений (в том числе случайных), или вводом необходимых значений.

1. Определите сумму элементов массива, расположенных до минимального.

2. Определите сумму элементов массива, расположенных до максимального.

3. Определите сумму элементов массива, расположенных между минимальным и максимальным значениями.

4. Определите сумму элементов массива, расположенных до минимального значения.

5. Определите сумму элементов массива, расположенных до максимального значения.

6. Определите сумму элементов массива, расположенных после максимального значения.

7. Определите сумму элементов массива, расположенных после максимального по модулю значения.

8.Определите сумму элементов массива, расположенных после минимального по модулю значения.

9.Определите сумму элементов массива, расположенных до минимального по модулю значения.

10. Найти сумму чисел, расположенных между максимальным и минимальным элементами (включая сами числа).

11. Найти сумму чисел, расположенных между максимальным и минимальным по модулю элементами (не включая сами числа).

12. Найти сумму чисел, расположенных между минимальным положительным и максимальным отрицательным элементами (включая сами числа).

Индексы одномерных массивов

Для тестирования предусмотреть возможность задавать элементы массива различным образом: при описании с инициализацией, присвоением значений (в том числе случайных), или вводом необходимых значений.

1. Вывести на экран все числа заданной последовательности, индексы которых есть степени двойки. Определить в заданной последовательности целых чисел количество чисел, которые являются степенью двойки.

2. Вывести на экран все числа заданной последовательности, индексы которых есть степени тройки. Определить в заданной последовательности целых чисел количество чисел, которые являются степенью тройки.

3. Вывести на экран элементы последовательности, индексы которых являются степенями пятерки. Определить в заданной последовательности целых чисел количество чисел, которые являются степенью пятерки.

4. Вывести на экран все числа заданной последовательности, индексы которых есть полные квадраты. Определить в заданной последовательности целых чисел количество чисел, которые являются полными квадратами.

5. Вывести на экран все числа заданной последовательности, индексы которых есть простые числа. Определить в заданной последовательности целых чисел количество чисел, которые являются простыми числами.

6. Вывести на экран все числа заданной последовательности, индексы которых есть числа Фибоначчи. Определить в заданной последовательности целых чисел количество чисел Фибоначчи.

7. Получить: max (a₁ + a_n, a₂ + a_n-1, ..., a_n/2 + a_n/2+1).

8. Получить: min (a₁ + a_n, a₂ + a_n-1, ..., a_n/2 + a_n/2+1).

9. Получить: a₁a₂ + a₂ a₃ + … + a_n-1 a_n + a_n a₁.

10. Определить количество инверсий в последовательности (количество X_i > X_j при i < j).

11. Вывести на экран все элементы, встречающиеся в последовательности ровно один раз.

12. Вывести на экран все элементы, встречающиеся в последовательности ровно два раза.