Формальные средства и алгоритмы анализа и моделирования динамических систем

Определитель матрицы

Определителем (или детерминантом) квадратной матрицы 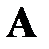размера 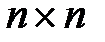называется число 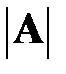, получаемое по формуле:

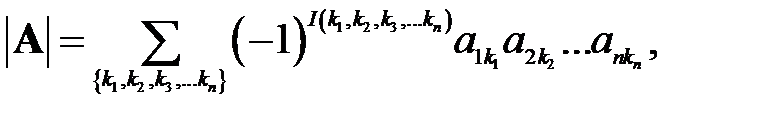
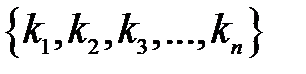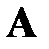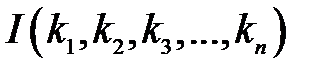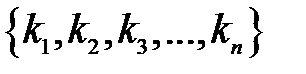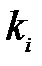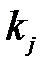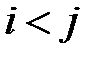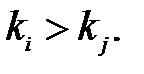где – всевозможные различные перестановки, образованные из номеров столбцов матрицы , – полное число инверсий в перестановке . Инверсией будем называть такое взаимное расположение чисел и в перестановке, при котором выполняются условия и Например, 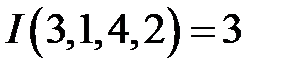. Общее число перестановок, определяющее количество слагаемых в приведенной сумме, равно .

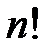Напомним основные свойства определителей, важных с точки зрения последующего рассмотрения некоторых численных методов:

1. При транспонировании матрицы ее определитель не меняется.

2. При перестановке двух столбцов или двух строк матрицы знак ее определителя меняется на противоположный.

3. Определитель матрицы, содержащей два линейно-зависимых столбца (или строки), равен нулю.

4. Определитель произведения матриц размера 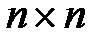равен произведению их определителей, то есть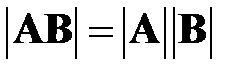

Детерминант квадратной матрицы порядка k, образованной элементами, стоящими на пересечении строк 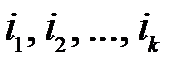и столбцов 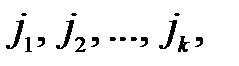называется минором k -го порядка и обозначается .

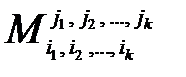Детерминант квадратной матрицы порядка 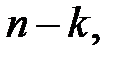образованной элементами, остающимися после вычеркивания строк 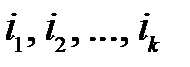и столбцов 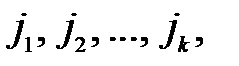называется минором, дополнительным к минору 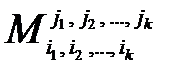, и обозначается .

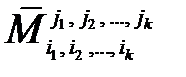Число 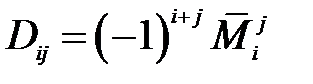называется алгебраическим дополнением элемента 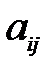матрицы 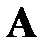, где 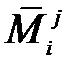– дополнительный минор элемента 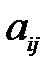. Справедливы следующие равенства:

,

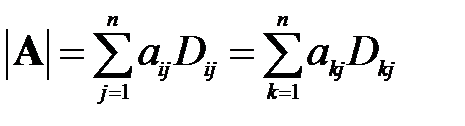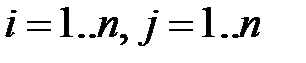
Разложение определителя по i -ой строке имеет вид:

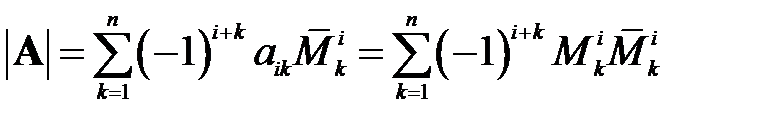
Наивысший из порядков, отличных от нуля миноров матрицы 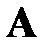, называется рангом матрицы и обозначается 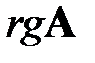. Очевидно, что если определитель матрицы не равен нулю, то её ранг равен количеству строк (столбцов), т.е. порядку матрицы.

Процедуры вычисления определителя, миноров, ранга матриц могут использоваться в анализе динамических систем, например, при проверке критерия устойчивости системы [2], условия её наблюдаемости в алгоритмах оптимальной фильтрации [3] и т.д.

LU-разложение матриц

Общепринятые обозначения L и U связаны с английскими словами «lower» (нижний) и «upper» (верхний). Существует другой вариант обозначения: L и R, определяемый словами «left» (левый) и «right» (правый).

LU-метод основан на том, что если главные миноры матрицы 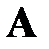отличны от нуля, тогда эту матрицу можно представить, причем единственным образом, в виде произведения:

,

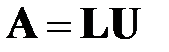где 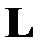– нижняя (левая) треугольная матрица с ненулевыми диагональными элементами и 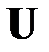– верхняя (правая) треугольная матрица с единичной диагональю:

, ,

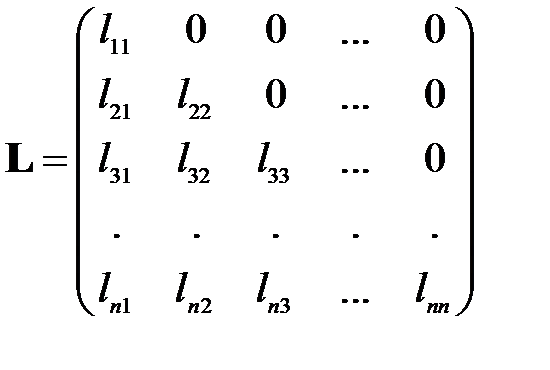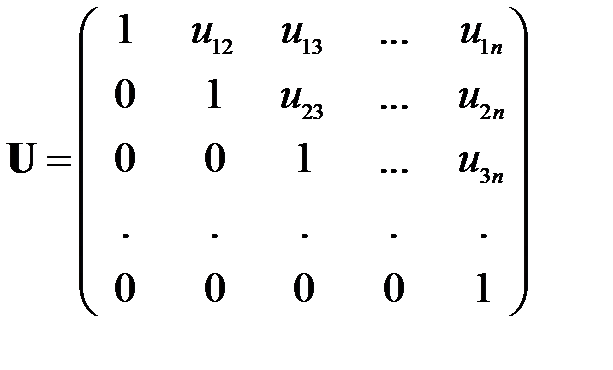или:

,

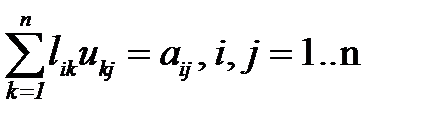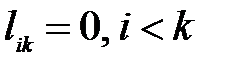
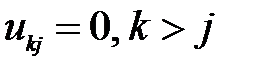
Окончательно можно записать:

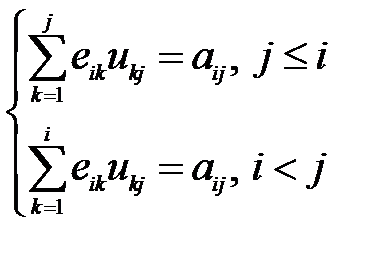
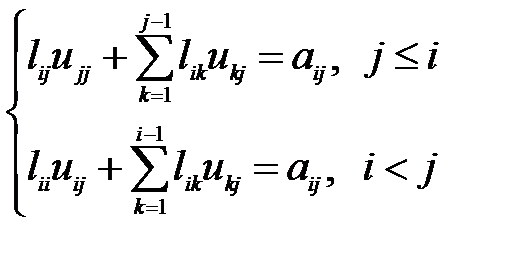
Полагая 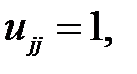получим следующие рекуррентные формулы для вычисления элементов матриц 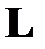и :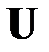

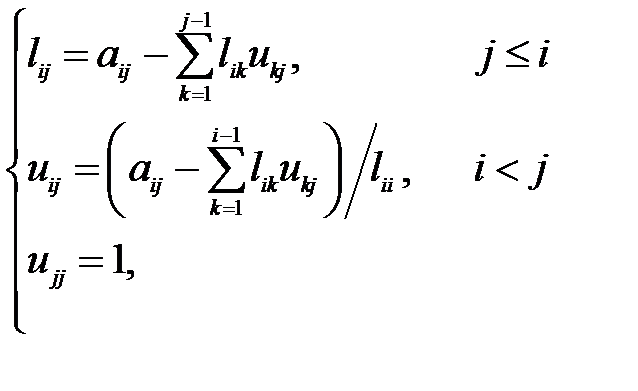
Вычисления следует начинать с левого верхнего элемента и выполнять построчно, слева направо. Вычислительная сложность данного алгоритма составляет .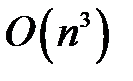

С использованием найденных элементов матриц 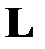и 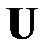становится возможным простое вычисление определителя исходной матрицы :

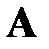Обратные матрицы

Обратной матрицей для матрицы 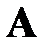называется такая матрица 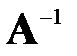, при умножении на которую исходная матрица 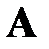даёт в результате единичную матрицу 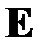, т.е.выполняется равенство: .

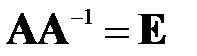Обратные матрицы часто используются в методах и алгоритмах моделирования процессов функционирования интегрированных систем ЛА, в частности, в алгоритмах оптимального оценивания, где такие матрицы играют роль весовых коэффициентов, определяющих, например, степень актуальности и достоверности некоторой апостериорной информации [3].

Литература

1. Амелькин Н.И. Кинематика и динамика твердого тела (кватернионное изложение). – М.: МФТИ (ГУ), 2000. – 64 с.

2. Бесекерский В. А., Попов Е.П. Теория Систем автоматического управления. – Изд. 4-е, перераб. и доп. – Спб.: Профессия, 2003. – 752 с.

3. Бобронников В. Т., Красильщиков М. Н., Козорез Д. А. и др. Статистическая динамика и оптимизация управления летательных аппаратов: учебное пособие. / Под общ. ред. М. Н. Красильщикова, В. В. Малышева. – Изд. 2-е, перераб. и доп. – М.: Альянс, 2013. – 468 с.

4. Бранец В. Н., Шмыглевский И. П. Применение кватернионов в задачах ориентации твердого тела. – М.: Наука, 1973. – 320 с.

5. Вержбицкий В.М. Основы численных методов: Учебник для вузов. – М.: Высшая школа, 2002. – 840 с.

6. Желтов С.Ю., Веремеенко К.К., Ким Н.В. и др. Современные информационные технологии в задачах навигации и наведения беспилотных маневренных летательных аппаратов. / Под ред. М.Н. Красильщикова, Г.Г. Себрякова. – М.: ФИЗМАТЛИТ, 2009. – 556 с.

7. Осипов Д.Л. – Delphi. Программирование для Windows, OS X, iOS и Android. – Спб.: БХВ-Петербург, 2014. – 464 с.

8. Рашевский П. К. Риманова геометрия и тензорный анализ. – М.: Наука, 1967. – 664 с.

9. Страуструп Б. Программирование: принципы и практика с использованием С++. – Второе издание. – М.: Вильямс, 2016. – 1328 с.

10. Умнов А. Е., Аналитическая геометрия и линейная алгебра: учебное пособие. – 3-е изд., испр. и доп. – М.: МФТИ, 2011. – 554 с.

11. Элджер Дж. С++: Библиотека программиста. – Спб.: Питер, 1999. – 320 с.

[1] Более подробно основные понятия и определения линейной алгебры рассматриваются, например, в [10].

[2] Строго говоря, такая интерпретация допустима и для 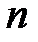-мерного однородного гиперпространства, но в задачах моделирования процессов функционирования интегрированных систем ЛА такое обобщение, как правило, излишне.

Формальные средства и алгоритмы анализа и моделирования динамических систем

При описании процессов функционирования различных динамических систем (к которым относятся и бортовые интегрированные системы ЛА) в качестве базовых формальных средств, на которых основана запись математических выражений, используются векторы и матрицы.

В математическом моделировании вектор может рассматриваться в разных интерпретациях. Например, в трёхмерном евклидовом пространстве под вектором понимают математический объект, характеризующийся величиной и направлением. Такой вектор всегда имеет некоторый физический смысл (радиус-вектор, вектор скорости, вектор силы, вектор напряженности электрического поля и т.д.). Если в пространстве задана система координат, то вектор однозначно определяется тремя числами – координатами, например: . 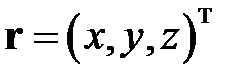.. Над множеством векторов в таком пространстве определен ряд алгебраических операций, таких как сложение, скалярное и векторное умножение, вычисление модуля, имеющих геометрический смысл и представление. Традиционно координаты векторов принято записывать в столбец, поэтому при строчной записи координат используется оператор транспонирования. Вектор в данной интерпретации является основным формальным средством описания движения ЛА и процессов функционирования связанных с его движением интегрированных систем.

В наиболее общем смысле вектор может рассматриваться как элемент некоторого 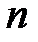-мерного линейного пространства, представляющий собой упорядоченную последовательность из . 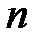. чисел – координат (вектор размерности 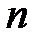): 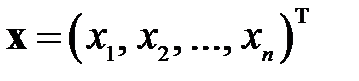. В таком смысле векторы используются в обобщённой теории динамических систем. Каждая такая система имеет некий набор параметров различной физической природы, характеризующих её состояние. Реально существующая система может иметь бесконечное или очень большое число таких параметров, но при переходе к математической модели этой системы количество параметров ограничивают. Упомянутое линейное пространство, в котором представлено множество всех состояний динамической системы, определяемых возможными значениями параметров, называется фазовым пространством. Координаты этого пространства называются фазовыми переменными (переменными состояния). Совокупность таких координат образует вектор состояния системы. Для множества таких векторов в общем случае отсутствует геометрическая интерпретация, и, в отличие от трёхкомпонентных векторов, не определены некоторые алгебраические операции, имеющие чисто геометрический смысл (например, векторное произведение). В таком смысле вектор является основным средством формализации различных математических моделей, алгоритмов их исследования и анализа, процессов функционирования динамических систем.

Формализация математических моделей динамики интегрированных систем ЛА также опирается на понятие матрицы – упорядоченной прямоугольной таблицы чисел, в общем случае содержащей .. строк и 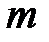столбцов (размерности 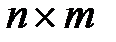). Если количество строк равно количеству столбцов, то такая матрица называется квадратной. Так, например, квадратная матрица размерности . 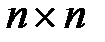. является естественной формой записи корреляционных моментов случайных компонент вектора состояния динамической системы 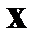, состоящего из 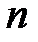компонент:

,

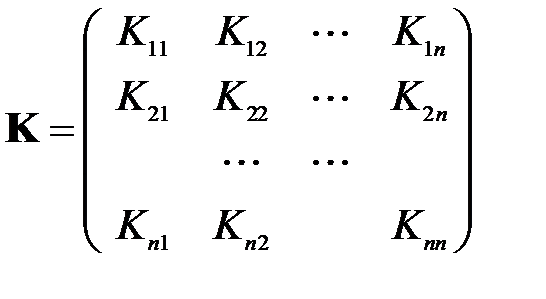где 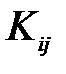– взаимный корреляционный момент 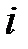-ой и -ой компоненты вектора состояния, причём 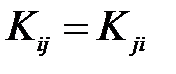. Матрица, для которой выполняется последнее условие, называется симметричной (симметрической).

Над множеством матриц и векторов определены линейные алгебраические операции, позволяющие существенно упростить формализацию и сделать более компактной запись математических моделей интегрированных систем ЛА, состояние которых определяется в многомерном фазовом пространстве. Формальная запись расчётных соотношений, задающих, например, динамику ЛА или составляющих какие-либо алгоритмы с использованием векторов и матриц требует владения основными понятиями линейной алгебры, знания правил сложения, умножения, преобразования и свёртки векторов и матриц. Для непосредственного проведения расчётов в процессе моделирования или анализа динамических систем необходимо владение основными численными методами, реализующими перечисленные процедуры.

Далее в этом разделе будут рассмотрены понятия и правила выполнения основных алгебраических операций над множеством векторов и матриц[1], а также некоторые численные методы и алгоритмы над матрицами с учётом их применения в моделировании и анализе динамики интегрированных систем ЛА.