Векторы на плоскости и в пространстве
7.1.Основные термины, формулы, положения
Геометрический вектор. Декартова система координат. Координаты вектора.
Модуль вектора, сложение, вычитание векторов, умножение на число, свойства линейных операций над векторами.
Скалярное, векторное, смешанное произведения векторов. Свойства этих операций.
7.2. Типовые задания по теме
1. Даны точки А, В, С и точка Д – середина отрезка ВС. Доказать: 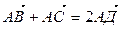 .
.
2. Дан параллелограмм АВСД, М – точка пересечения его диагоналей. Выразить 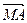 ,
, 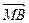 ,
, 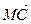 ,
, 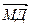 через
через 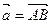 и
и 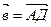 .
.
3. Точки М и К середины сторон параллелограмма АВСД. Разложить 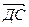 по векторам
по векторам 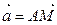 и
и 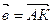 .
.
4. Дан куб ABCDEFGH. Разложить вектор 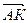 , где К- центр грани DHGC, по векторам
, где К- центр грани DHGC, по векторам 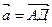 ,
, 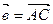 и
и 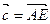 .
.
5. Отрезок СД разделен на три равные части. Найти координаты точек деления, если координаты точек: С(6; 0) и Д (3; -4).
6. Найти длину вектора 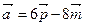 при условии, что
при условии, что 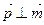 и
и 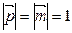 .
.
7. При каких значениях 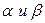 :
:
1) вектор 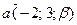 коллинеарен вектору
коллинеарен вектору 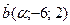 ;
;
2) векторы 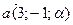 и
и 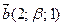 перпендикулярны, если
перпендикулярны, если 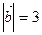 ?
?
8. В плоскости XOY найти вектор, перпендикулярный 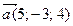 и имеющий одинаковую с ним длину.
и имеющий одинаковую с ним длину.
9. Даны вершины треугольника А(1; 2), В(3; 4) и С(6; 2). Найти внутренний угол при вершине А и площадь треугольника.
10. Дан параллелограмм АВСД, три вершины которого заданы координатами: А(-1; -2; 3), В(-4; 1; 2), С(5; 2; 7). Найти четвертую вершину Д, острый угол параллелограмма и его площадь.
11. Являются ли точки А(3; -1; 2), В(1; 2; 3), С(-1; 1; -3) и Д(3; -5; 3) вершинами трапеции? Можно ли провести через эти точки плоскость?
12. Найдите угол между диагоналями AC и BД четырехугольника, заданного своими вершинами: А(6; -1; 4), B(1; -1; 4), С(1; 2; 0), Д(6; 2; 0).
13. Найти объем параллелепипеда, построенного на векторах 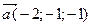 ,
, 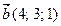 ,
, 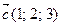 , имеющих общее начало.
, имеющих общее начало.
7.3. Дополнительные задания по теме
1. В треугольнике 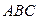 точки
точки 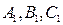 являются серединами сторон. Доказать, что для произвольной точки О выполняется равенство
являются серединами сторон. Доказать, что для произвольной точки О выполняется равенство 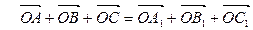 .
.
2. Дан правильный шестиугольник 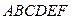 . Принимая за базисные векторы
. Принимая за базисные векторы 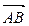 и
и 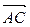 , найти в этом базисе координаты векторов
, найти в этом базисе координаты векторов 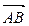 ,
, 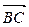 ,
, 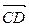 ,
, 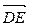 ,
, 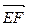 ,
, 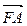 .
.
3. Определить, при каких значениях 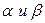 вектор
вектор 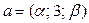 будет коллинеарен вектору
будет коллинеарен вектору 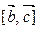 , если
, если 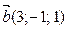 и
и 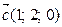 .
.
4. Объем тетраэдра АВСД равен 5 куб.ед., три его вершины имеют координаты: A(2; 1; -1), B(3; 0; 1), C(2; -1; 3). Найти координату четвертой вершины, если известно, что она лежит на оси OY.
8. Уравнения линии на плоскости
8.1.Основные термины, формулы, положения
Уравнение линии. Различные уравнения прямой: уравнение прямой, заданной точкой и направляющим вектором; уравнение прямой, заданной двумя точками; уравнение «в отрезках»: уравнение прямой, заданной точкой и вектором нормали; уравнение с угловым коэффициентом; общее уравнение прямой.
Взаимное расположение двух прямых на плоскости; условия параллельности прямых. Угол между прямыми. Условие перпендикулярности.
Кривые второго порядка: окружность, эллипс, гипербола, парабола. Канонические уравнения кривых второго порядка. Общее уравнение кривой второго порядка.
8.2. Типовые задания по теме
1. Даны три последовательные вершины параллелограмма A(2; 3), B(-1; 1), C(4; -2). Написать уравнения прямых, содержащих стороны и диагонали параллелограмма.
2. Дано общее уравнение прямой 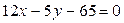 . Написать для этой прямой: а) уравнение с угловым коэффициентом; б) уравнение «в отрезках».
. Написать для этой прямой: а) уравнение с угловым коэффициентом; б) уравнение «в отрезках».
3. Издержки производства 100 штук некоторого товара составляют 300 руб, а 500 штук – 600 руб. Определить издержки производства 400 штук товара при условии, что функция издержек линейна.
4. Напишите уравнение прямой, проходящей через точку А пересечения прямых 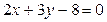 и
и 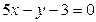 и точку В пересечения прямых
и точку В пересечения прямых 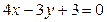 и
и 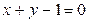 .
.
5. Через точку пересечения прямых 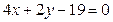 и
и 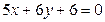 проведена прямая, перпендикулярная прямой
проведена прямая, перпендикулярная прямой 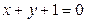 . Напишите ее уравнение.
. Напишите ее уравнение.
6. Прямая L задана уравнением: 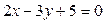 . Составить уравнение прямой, проходящей через точку М(4; -5) так, чтобы она была:
. Составить уравнение прямой, проходящей через точку М(4; -5) так, чтобы она была:
1) параллельна прямой L; 2) перпендикулярна прямой L.
7. Середины сторон треугольника ABC находятся в точках P(5, 3), Q(-1, 5) и S(1, 6). Найдите координаты его вершин.
8. Дан треугольник с вершинами в точках A(3; 6), B(-1; 3), C(2; -1). Вычислить длину его высоты, проведенной из вершины С.
9. Найти расстояние от прямой 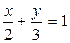 до начала координат.
до начала координат.
10. Вычислить площадь треугольника, отсекаемого прямой 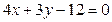 от координатного угла.
от координатного угла.
11. Вычислите величины углов треугольника, стороны которого в прямоугольной системе координат заданы уравнениями: 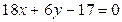 ;
; 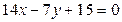 ;
; 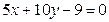 .
.
12. Изобразить в прямоугольной системе координат область, определяемую системой:
а) 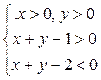 ; б)
; б) 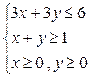 ; в)
; в) 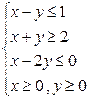 ; г)
; г) 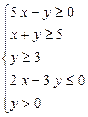 .
.
13. Найти координаты центра и радиус окружности: 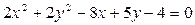 .
.
14. Даны вершины треугольника A (5, 6), В (3, 4) и С (9, 1). Найдите центр описанной около него окружности.
15. Составить уравнение окружности:1) проходящей через точки А(3; 1) и В(-1; 3), если ее центр лежит на прямой 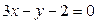 ; 2) проходящей через точки А(5; 0) и В(1; 4), если ее центр лежит на прямой
; 2) проходящей через точки А(5; 0) и В(1; 4), если ее центр лежит на прямой 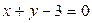 .
.
16. Составить каноническое уравнение эллипса и построить его в системе координат, если: 1) заданы полуоси эллипса 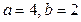 ; 2)
; 2) 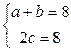 .
.
17. Доказать, что уравнение 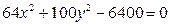 задает эллипс. Найти координаты его фокусов, полуоси, эксцентриситет.
задает эллипс. Найти координаты его фокусов, полуоси, эксцентриситет.
18. Ординаты всех точек окружности 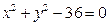 сокращены втрое. Составить уравнение полученной новой кривой.
сокращены втрое. Составить уравнение полученной новой кривой.
19. Доказать, что уравнение 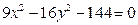 задает гиперболу. Найти координаты её фокусов, эксцентриситет. Построить данную кривую.
задает гиперболу. Найти координаты её фокусов, эксцентриситет. Построить данную кривую.
19. Написать каноническое уравнение гиперболы, проходящей через точку 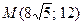 , если
, если 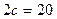 .
.
20. Составить уравнение гиперболы, центр которой совпадает с началом координат, а действительная ось – с осью OX, если угол между асимптотами равен 90° и гипербола проходит через точку 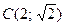 .
.
21. Составить каноническое уравнение параболы, если:
1) парабола симметрична относительно оси ОХ, расположена в левой полуплоскости и р = 2;
2) парабола симметрична относительно оси ОУ и проходит через точку С(1; 1).
22. Найти точки пересечения параболы 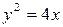 и прямых
и прямых 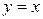 ,
, 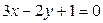 .
.
23. Составить уравнение параболы, симметричной относительно оси OX, если она проходит через точку М(-2; -3) и имеет вершину в начале координат. Найти её фокус и директрису.
24. Дана парабола 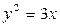 . Найти точки параболы, расстояния от которых до её фокуса равно 1.
. Найти точки параболы, расстояния от которых до её фокуса равно 1.
8.3. Дополнительные задания по теме
1.Через точку М(4;-3) прямоугольной системы координат, проведена прямая так, что площадь треугольника, образуемого ею и осями координат,
равна трем квадратным единицам. Найдите уравнение этой прямой.
2. Записать уравнения прямых, проходящих через вершины треугольника параллельно противолежащим сторонам, если треугольник образован пересечением прямых: 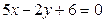 ,
, 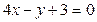 ,
, 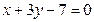 .
.
3. Найти площадь квадрата, если одна из его вершин – точка А(2; -5), а одна из сторон принадлежит прямой 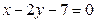 .
.
4. Диагональ квадрата расположена на прямой 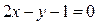 . Одна из его вершин находится в точке А(4, -3). Составьте уравнения сторон и второй диагонали этого квадрата.
. Одна из его вершин находится в точке А(4, -3). Составьте уравнения сторон и второй диагонали этого квадрата.
5. Найдите неравенства, задающие внутреннюю область треугольника АВС, если координаты точек: А(-1; 4), В(5; 2), С(1; 3).
6. Составить уравнение окружности, описанной около треугольника, стороны которого заданы уравнениями 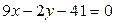 ,
, 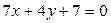 ,
, 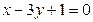 .
.
7. Составить уравнение гиперболы, фокусы которой находятся в вершинах эллипса 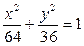 , а вершины – в фокусах данного эллипса.
, а вершины – в фокусах данного эллипса.
8. Какое множество точек на плоскости определяет уравнение:
1) 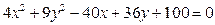 ;
;
2) 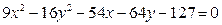 ;
;
3) 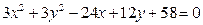 ;
;
4) 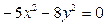 ; 5)
; 5) 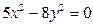 ?
?
