Линейные отображения векторных пространств
5.1.Основные термины, формулы, положения
Линейное отображение векторных пространств. Матрица линейного отображения. Собственные векторы и собственные значения линейного отображения. Ядро и дефект линейного отображения.
4.2. Типовые задания по теме
1. Выяснить, будет ли отображение 
пространства V в себя линейным, если 
для любого вектора 
.
2. Выяснить, будет ли отображение пространства 
в себя линейным, если:
а) 
;
б) 
.
В случае линейности: найдите матрицу данного отображения относительно стандартного базиса .
3. Найти собственные значения и соответствующие им собственные векторы линейного отображения пространства V над R, заданного в некотором базисе матрицей
а) 
; б) 
; в) 
; г) 
.
5.3.Дополнительные задания по теме
1. Известны векторы 
пространства V , заданные своими координатами в некотором базисе. В этом же базисе найдите матрицу линейного отображения, переводящего 
в 
соответственно, если 
, 
, 
, и при этом:
а) 
;
б) 
.
2. Показать, что дифференцирование является линейным отображением линейного пространства многочленов степени не превосходящей n с одной переменной над полем R в себя. Найти матрицу этого отображения в базисе 
.
6.Линейные математические модели в экономике
6.1.Основные термины, формулы, положения
Структурная матрица торговли. Линейная модель обмена (модель международной торговли).
Вектор валовой продукции, вектор конечной продукции, матрица затрат (технологическая матрица), продуктивная матрица, коэффициенты прямых затрат. Модель Леонтьева.
Модель производственной системы. Задача планирования производства.
Задача линейного программирования. Область допустимых решений. Графическое решение задачи линейного программирования.
6.2. Типовые задания по теме
1. Структурная матрица торговли четырех стран имеет вид: 
Найти бюджеты этих стран, удовлетворяющие сбалансированной бездефицитной торговле при условии, что сумма бюджетов равна 6270 усл.ден. ед.
2. Для четырёх предприятий отрасли вектор выпуска продукции и матрица внутреннего потребления имеют вид 
, 
. Найти вектор объемов конечного продукта, предназначенного для реализации вне отрасли.
3. Структурная матрица торговли трех стран имеет вид 
. Найти бюджеты первой и второй стран, удовлетворяющие сбалансированной бездефицитной торговле при условии, что бюджет третьей страны равен 1100 усл. ед.
4. Вектор совокупного продукта (выпуска продукции) 
, матрица коэффициентов прямых затрат (матрица внутреннего потребления) 
. 1) Найти вектор конечного продукта. 2) Найти необходимый совокупный продукт, если матрица конечного продукта 
.
5. Дана матрица коэффициентов прямых затрат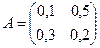 
. 1) Найти вектор совокупного продукта X для обеспечения выпуска конечной продукции 
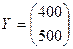. 2) Найти приращение вектора 
для увеличения выпуска конечной продукции на 
.
6. Составить математическую модель задачи. Из пункта А в пункт В ежедневно отправляются скорые пассажирские поезда. Наличный парк вагонов разных типов, из которых ежедневно можно комплектовать данные поезда, и число пассажиров, вмещающихся в каждом из вагонов, приведены ниже.
| Вагон | Число вагонов в поезде | Число пассажиров | Парк вагонов | |
| Скором | Пассажирском | |||
| Багажный | – | |||
| Почтовый | – | – | ||
| Плацкартный | ||||
| Купированный | ||||
| Мягкий |
Определить количество скорых и пассажирских поездов, при которых число перевозимых пассажиров достигает максимума.
7. Предприятие для выпуска некоторой продукции использует две технологии (два способа). При этом необходимы три вида ресурсов. Известно: запасы ресурсов; затраты каждого вида ресурса за 1час работы с использованием каждой технологи; прибыль предприятия от реализации продукции, выпускаемой за 1 час работы с использованием каждой технологии; общее время работы предприятия по обеим технологиям (500 часов).
| Вид ресурса | Запасы ресурса, ед. | Затраты ресурсов за 1 ч работы по технологии | |
| №1 | №2 | ||
| Прибыль, руб/ч |
Сколько времени по каждой технологии должно работать предприятие, чтобы обеспечить максимум прибыли от реализации выпускаемой продукции?
8. Решить графически задачу линейного программирования (ЗЛП):
; 
; 
; 
.
6.3. Дополнительные задания по теме
1. Листы материала размером 6м 
13м нужно раскроить так, чтобы получились заготовки двух типов: 800 шт. типа А размером 4м 5м и 400 шт. типа В размером 2м 3м., израсходовав при этом как можно меньше материала.
2. Решить ЗЛП: 