Арифметическое n-мерное пространство
3.1.Основные термины, формулы, положения
Арифметический n-мерный вектор. Линейные операции над арифметическими векторами, их свойства.
Линейная комбинация. Линейная зависимость системы векторов. Линейная независимость системы векторов. Базис системы векторов. Ранг системы векторов. Ранг матрицы.
Арифметическое n-мерное пространство: определение, базис, свойства. Разложение вектора по базису, Координаты вектора.
Приложения теории арифметического векторного пространства: критерий совместности системы линейных уравнений; пространство решений однородной системы линейных уравнений; фундаментальный набор решений.
3.2. Типовые задания по теме
1. Найти линейную комбинацию арифметических векторов:
а) 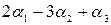 , если
, если 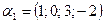 ,
, 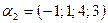 ,
, 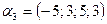 ;
;
б) 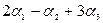 , если
, если 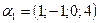 ,
, 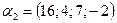 ,
, 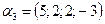 .
.
2. Найти вектор x из уравнения 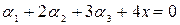 , если
, если 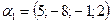 ,
, 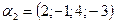 ,
, 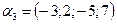 .
.
3. Будет ли данная система векторов линейно зависимой:
а) 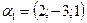 ,
, 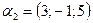 ,
, 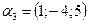 ;
;
б) 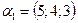 ,
, 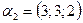 ,
, 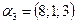 ;
;
в) 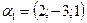 ,
, 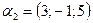 ,
, 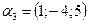 ,
, 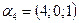 ?
?
4. Доказать: а) система векторов, содержащая два равных вектора, линейно зависима; б) система векторов, два вектора которой различаются скалярным множителем, линейно зависима.
5. Образуют ли векторы 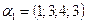 ,
, 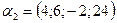 ,
, 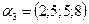 ,
, 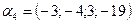 базис пространства R4?
базис пространства R4?
6. При помощи элементарных преобразований найти ранги матриц:
а) 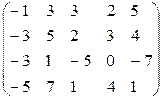 ; б)
; б) 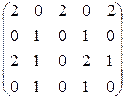 ; в)
; в) 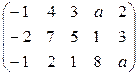
(в зависимости от а).
7. Как может измениться ранг матрицы, если приписать к ней: а) одну строку, б) две строки?
8. Исследовать на совместность системы линейных уравнений:
а) 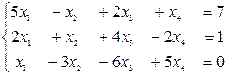 ; б)
; б) 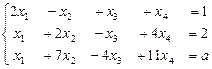
9. Описать множество решений однородной СЛУ, используя фундаментальный набор решений:
а) 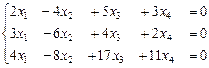 ; б)
; б) 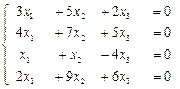 ;
;
в) 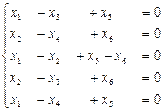 ; г).
; г). 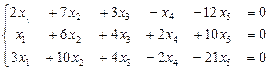 .
.
10. Найти базис и размерность векторного пространства решений однородной СЛУ: 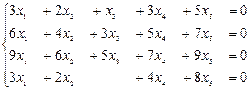 .
.
11. Является ли фундаментальным набором решений системы 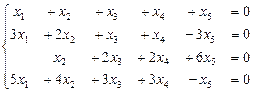 набор векторов:
набор векторов:
а) 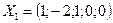 ,
, 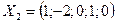 ,
, 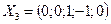 ,
, 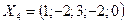 ;
;
б) 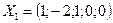 ,
, 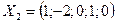 ,
, 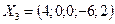 ?
?
12. Является ли вектор 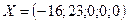 решением системы
решением системы 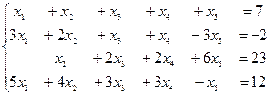 ?
?
Используя предыдущее задание №11, записать вектор общего решения для данной системы.
3.3. Дополнительные задания по теме
1. Найти все 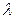 , при которых
, при которых 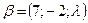 линейно выражается через векторы
линейно выражается через векторы 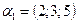 ,
, 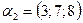 ,
, 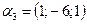 .
.
2.Выделить базис системы строк и найти выражения небазисных строк через базисные:
а) 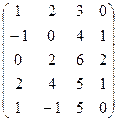 ; б)
; б) 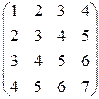 ; в)
; в) 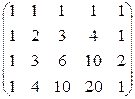 .
.
4. Векторные пространства
Евклидовы пространства
4.1.Основные термины, формулы, положения
Линейное векторное пространство. Базис и размерность векторного пространства. Свойства базиса.
Координаты вектора. Матрица перехода от базиса к базису. Координаты вектора в различных базисах.
Скалярное произведение векторов. Евклидовы пространства. Норма вектора. Угол между векторами. Ортонормированный базис.
4.2. Типовые задания по теме
1. Проверить, является ли векторным пространством над полем действительных чисел множество квадратных матриц 2-го порядка 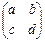 ,
, 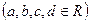 относительно операций сложения и умножения на число.
относительно операций сложения и умножения на число.
2. Проверить, является ли векторным пространством над полем действительных чисел множество линейных многочленов с действительными коэффициентами относительно операций сложения и умножения на число.
3. Является ли векторным пространством множество V всех векторов- решений однородной системы линейных уравнений с n переменными? Что является базисом этого пространства? Подпространством какого пространства является множество V?
4. Найти базис векторного пространства квадратных матриц 2-го порядка 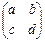 ,
, 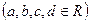
5. Доказать что арифметические векторы 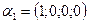 ,
, 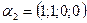 ,
, 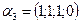 ,
, 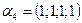 образуют базис пространства
образуют базис пространства 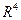 .. Разложить по этому базису вектор: а)
.. Разложить по этому базису вектор: а) 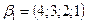 ; б)
; б) 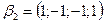 . Найти координаты этих же векторов в стандартном базисе
. Найти координаты этих же векторов в стандартном базисе 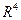 :
: 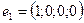 ,
, 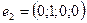 ,
, 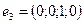 ,
, 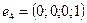 .
.
6. Найти матрицу перехода от базиса 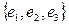 к базису
к базису 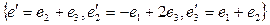 векторного пространства V.
векторного пространства V.
7. Найти матрицу перехода от базиса 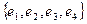 к базису
к базису 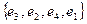 векторного пространства V
векторного пространства V
8. В базисе 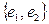 векторного пространства V даны векторы
векторного пространства V даны векторы 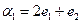 и
и 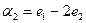 . Доказать, что векторы
. Доказать, что векторы 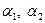 также образуют базис этого пространства. Найти координаты вектора
также образуют базис этого пространства. Найти координаты вектора 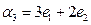 в базисе
в базисе 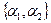 .
.
9. В базисе 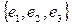 дан вектор
дан вектор 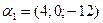 . Найти координаты этого вектора в базисе
. Найти координаты этого вектора в базисе 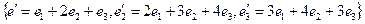 .
.
10. Дана матрица 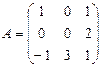 перехода от базиса
перехода от базиса 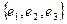 к базису
к базису 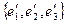 . Найти координаты векторов
. Найти координаты векторов 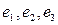 в базисе
в базисе 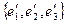 .
.
11. Пусть 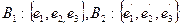 два базиса пространства R3 и
два базиса пространства R3 и 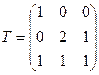 матрица перехода от В1 к В2. Найти: а) координаты вектора
матрица перехода от В1 к В2. Найти: а) координаты вектора 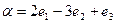 в базисе В2.; б) координаты вектора
в базисе В2.; б) координаты вектора 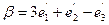 в базисе В1.
в базисе В1.
12. Вектор 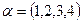 задан координатами в базисе В1, вектор
задан координатами в базисе В1, вектор 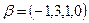 - в базисе В2 и
- в базисе В2 и 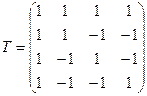 матрица перехода от В1 к В2. Найти координаты вектора
матрица перехода от В1 к В2. Найти координаты вектора 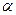 в базисе В2 и координаты
в базисе В2 и координаты 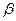 в базисе В1.
в базисе В1.
13. Вычислить скалярное произведение векторов 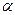 и
и 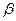 пространства
пространства 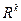 со стандартным скалярным произведением:
со стандартным скалярным произведением:
а) 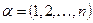 ,
, 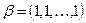 ,
, 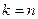 ;
;
б) 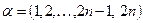 ,
, 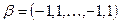 ,
, 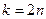 .
.
14. Найдите угол между векторами евклидова пространства R4 со стандартным скалярным произведением.
а) 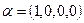 ,
, 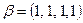 ;
;
б) 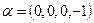 ,
, 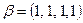 ;
;
в) 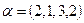 ,
, 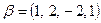 ;
;
15. Исследовать на ортогональность векторы 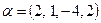 ,
, 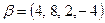 стандартного евклидового пространства R4. Являются ли они нормированными?
стандартного евклидового пространства R4. Являются ли они нормированными?
16. Образует ли ортогональный базис в R4 система векторов: 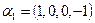 ,
, 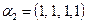 ,
, 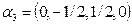 ? Постройте с помощью этой системы ортонормированный базис этого пространства.
? Постройте с помощью этой системы ортонормированный базис этого пространства.
4.3.Дополнительные задания по теме
1. Докажите, что в пространстве вещественных квадратных матриц 2-го порядка над полем R подмножество матриц вида 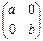
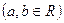 является его подпространством, а система векторов
является его подпространством, а система векторов 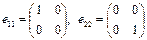 базисом этого подпространства.
базисом этого подпространства.
2. Докажите, что для любых векторов 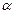 и
и 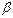 евклидова пространства верны утверждения: а)
евклидова пространства верны утверждения: а) 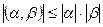 ; б)
; б) 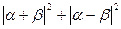 =
= 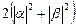 .
.
3. Ортогонализируйте системы векторов, заданных своими координатами в некотором ортонормированном базисе: а) 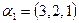 ,
, 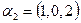 ,
, 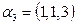 ; б)
; б) 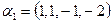 ,
, 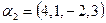 ,
, 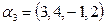 .
.
4. Пусть V – конечномерное векторное пространство над полем R, 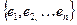 - некоторый базис V,
- некоторый базис V, 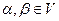 ,
, 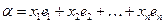 ,
, 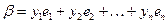 . Доказать, что скалярное произведение может быть определено следующим образом: а)
. Доказать, что скалярное произведение может быть определено следующим образом: а) 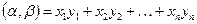 ; б)
; б) 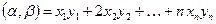 .
.
