Grammar: the subjunctive mood.
The Subjunctive Mood shows that the action or state expressed by the verb is presented as non-fact, as something imaginary, or desired. The Subjunctive mood is also used to express an emotional attitude of the speaker to real facts.
| Subject Clause | Expresses | |
| It is necessary Необходимо, It is important (recommended, advisable, requested, probable, strange, etc.) Важно, | that you (should) make a report. чтобы вы сделали доклад. that this law (should) be observed. чтобы этот закон соблюдался. | Supposition Necessity Probability Order Purpose Advice |
| Object Clause | ||
| I demand/demanded (order, advise, insist, suggest, require, propose, etc.) Я требую/потребовал, | that they (should) work together. чтобы они работали вместе. |
Ex. 1. Translate the sentences into Russian.
1. It is extremely important that you should carry out as many exercises as possible, no matter how trivial some of them may seem. 2. It is essential that the students should know all the rules. 3. I demand that they employ the differential calculus to deal with curves and surfaces. 4. He suggests that we deduce the properties of the curves involved by algebraic equations. 5. It is requested that the researcher (should) complete the calculations next week. 6. He advised that the students (should) inscribe a regular n-gon in a circle. 7. She proposed to her group-mates that they (should) discuss the topics of the term papers.
In Object Clause, introduced by the conjunction lestwe useshould for all persons.
She fears (feared) lest her secret should be discovered.
Она боится, чтобы ее секрет не был раскрыт.
Object Clause (after wish)
| Unreal Present I wish (if only) + Past Tense | Use |
| I wish (if only) you worked more efficiently. Я бы хотел, чтобы вы работали более эффективно. We wish (if only) we were not so busy now. Если бы только мы не были так заняты сейчас. | Regret about the present situation |
| I wish I could drive a car. Жаль, что я не умею водить машину. | Regret in the present concerning lack of ability |
| Unreal Past I wish (if only) + Past Perfect | |
| I wish I had attended the seminar yesterday. Жаль, что я не пришел на семинар вчера. | Regret that something happened or didn’t happen in the past |
| I wish (if only) + subject + would +Indefinite Infinitive | |
| I wish he would calculate more carefully. Хотелось бы, чтобы вы делали вычисления более внимательно. I wish it would stop raining. Я бы хотел, чтобы дождь прекратился. | Wish for a future change unlikely to happen, or annoyance |
Ex. 2. Translate the sentences from English into Russian.
1. I wish I knew the dimension of the body to calculate its volume.
2. I wish they had solved the three famous construction problems under the specified condition.
3. I wish I had written the test better, I have to revise the material again.
4. I wish he would stop working, he is very tired.
5. I wish I could understand the theory better.
6. I wish a new experiment would be started in our laboratory this month.
7. If only I were as good as you at mathematics.
8. I wish I had invited more people to the party.
9. If only you had taken his advice when he gave it.
Attributive clauses modifying the now “time” in the main clause
It is (high, about)time … Пора … (давно пора, уже пора)
It is time we left for the University, our classes start at 8.15.
Пора уходить в университет, наши занятия начинаются в 8.15.
1. It’s time we went there.
2. It’s time you learnt you’re a student of Mechanics and Mathematics Faculty.
3. It’s high time you made up mind!
4. It’s about time you obtained the expected result.
Comparison clause(as if …, as though…)
| It is as cold as if it were winter. Холодно, как будто сейчас зима. He looks as if he were very tired. Он выглядит так, как если бы он очень устал. | Present |
| He spoke as though she had known about it long before that day. Он говорил, как если бы он знал об этом задолго до этого дня. | Past |
Had better = should
| I had better + Present Infinitive You had better give up smoking. Вам бы лучше бросить курить. | Present, Future reference |
| It would have been better if+ Past Prefect It wouldhavebeenbetter if you hadn’t said that. Было бы лучше, если бы вы это не говорили. | Past reference |
Would rather = I’d prefer
| I’d rather smb. +Past Simple I’d rather smb. +Past Perfect I’d rather you studied a little harder. Лучше бы вы учились немного усерднее. I’d rather you had read the book last term. Лучше бы вы прочитали эту книгу в прошлом семестре. | Present, Future reference Past reference |
Ex. 3. Translate the sentences from English into Russian.
1. I wish I weren’t having my final test tomorrow. 2. I’d rather you hadn’t spoken so rudely to him. 3. The man speaks as if he had never heard of this country. 4. He acts as though he owned the house. 5. It’s time we went to the students’ canteen. 6. I had better obtain the necessary information using the Internet. 7. He looks as if he were impressed by the news. 8. The teacher advised that the students discuss the material in detail. 9. I’d rather you didn’t keep asking me every time you have a problem. 10. We worked slowly lest the task should have many mistakes.
Ex. 4. Put the verbs into the correct form.
1. We’d better (to take) some money for a taxi in case we (to miss) the last bus home. 2. Would you rather (to write) in ink or in pencil? 3. I’d rather you (not/mention) this anyone until next week. 4. He didn’t win the prize, but the looked as though he (to win) one. 5. It’s about time you (to go) on holiday. 6. Helen went to France this year, but she says she would rather (to go) to Spain. 7. You had better (not to speak) to me like that again. 8. I wouldn’t argue with her if I (to be) you. 9. If only I (not to drink) so much coffee. 10. I wish I (to listen) to you but I didn’t. 11 It’s essential that these conditions (to be satisfied).
Ex. 5. Translate from Russian into English.
1. Важно, чтобы студенты работали в компьютерных классах. 2. Странно, что он всегда опаздывает. 3. Желательно, чтобы вы выполнили это задание как можно скорее. 4. Я настаиваю, чтобы вы написали эту статью. 5. Жаль, что я не знал об этой научной конференции, я бы хотел послушать доклады по аналитической геометрии. 6. Он выглядит так, как если бы он провел свой отпуск на юге. 7. Пора бы знать такие простые истины! 8. Ты бы лучше купил билет на этот концерт заранее. 9. Я бы предпочел побыть сейчас один. 10. Ах, если бы только я тогда сделал правильный выбор!
Ex. 6. Complete the sentences.
1. It is probable that the question …
2. If I were you …
3. I’ll dictate slowly lest you …
4. It seems as if …
5. I shall go to the theater with pleasure unless …
6. It’s time they …
Pre- Reading Activity
Guess the meaning of the following words:
Differentiate [dIfq'renSieIt] converse (adj) [kOn´vWs]
function [´fANkS(q)n] actual [´xktjuql]
constant [´kOnst(q)nt] coordinate [kou´Ld(I)nIt]
identical [aI´dentik(q)l] associate (v) [q´souSIet]
complex [´kOmpleks] integrate [´IntIgreIt]
finally [´faInqlI] cylinder [´sIlIndq]
isolated [´aIsq`leItId] distance [´dIstqns]
familiar [fq´mIlIq]
Read and learn the following words:
| surface (n) | ['sWis] | поверхность |
| double (a) | [dAbl] | двойной |
| consist (v) (of) | [kqn'sIst] | состоять |
| unit (n) | ['ju:nIt] | единица |
| impose (v) | [im'pouz] | налагать (условие) |
| homogeneous (a) | ["hOmq'dZJnIqs] | однородный |
| miss (v) | [mIs] | отсутствовать |
| generator (n) | ['GenqreItq] | образующая |
| exhibit (v) | [Ig'zIbIt] | показывать, проявлять |
| transpose(v) | [trxns'pouz] | переставлять, переносить |
| vanish(v) | ['vxnIS] | исчезать, стремиться к нулю |
| degenerate(a) | [dI'Gen(q)rIt] | вырожденный |
| rule out (v) | [ru:l'aut] | исключать |
| further more (adv) | ['fWDq'mL] | кроме того, к тому же |
| imply (v) | [im'plaI] | подразумевать, означать |
| arbitrary (a) | ['RbItrqrI] | произвольный |
| elimination (n) | [I"lImI'neIS(q)n] | удаление, исключение (неизвестного) |
| vice versa | ['vaIsI'vWsq] | наоборот, обратно |
| jacobian (n) | [Gq'koubIqn] | якобиан |
| desire (v) | [dI'zaIq] | желать, испытывать желание |
| infinite (a) | ['InfInIt] | бесконечный |
| infinity (n) | [In'fInItI] | бесконечность |
| to set equal to | ['set'Jkwql] | положить равным |
| respectively (adv) | [rIs'pektIvlI] | соответственно, в указанном порядке |
| proper | ['prOpq] | собственный |
TEXT A
SURFACES
A surface can be described as a two-parameter family, or double infinity, of points. A surface can also be said to be the locus of a point moving with two degrees of freedom.
One method of representing a surface analytically consists in first establishing the usual left-handed orthogonal cartesian coordinate system with the same unit of distance on all three axes and then imposing one condition on a variable point P (x, y, z) by an equation of the form
F(x, y, z) = 0 (l. l)
Such an equation is called the implicit equation of the surface represented by it.
Certain very simple types of surfaces are already familiar. For example, if the equation (1.1) is linear in the variables x, y, z the surface represented by it is a plane, which is the simplest surface of all. Perhaps the next simplest surface is the sphere. If the equation (1.1) is homogeneous in x, y, z it represents a cone which vertex is at the origin. Finally, if one of the variables is missing from the implicit equation of a surface, the surface is a cylinder whose generators are parallel to the axis of the missing variable.
If the implicit equation (1.1) be solved for one of the variables as a function of the other two, say for z as a function of x, y, the resulting equation
z = f(x, y), (1. 2)
represents the same surface as before. Such an equation is called the explicit equation of the surface represented by it. The explicit equation (1.2) can be exhibited as a special case of the implicit equation (1.1) by transposing z to the right member and placing
F ( x, y, z) = f ( x, y)-z
Although for some purposes the implicit and explicit equations of surfaces are very useful, the definition of a real proper analytic surface will be based on a parametric representation.
Definition 1. Let the coordinates x, y, z of a point P be given as a single-valued analytic function of two real independent variables u, v on a rectangle T in a uv-plane by equations of the form
x=х(u, v), y=y(u, v), z=z(u, v) (1.3)
Further, let the jacobians of x, y, z with respect to u, v be denoted by J1, J2 , J3 so that
J1=yu z v- yv z u , J2=zu x v- zv x u ,J3=xu y v- xv y u(xu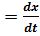 
,…) (1.4)
and suppose that not all of J1,J2,J3 vanish identically on the rectangle T. Then the locus of the point P, as u, v vary on T, is a real proper analytic surface.
Equations (1.3) are called parametric equations of the surface S, the parameters being the variables u, v. We reserve the right to permit the parameters to take on complex values. Moreover, one or more of the coordinates x, y, z may, under suitable conditions, be allowed to be complex. Tо say that a surface is proper means that it does not reduce to a curve. Both of these degenerate cases are ruled out by the hypothesis that the jacobians
J1= (1, 2, 3) do not all vanish identically. For, if the locus S were to reduce to a fixed point P, the coordinates x, y, z of P would all be constant, and the jacobians J1 would all vanish identically. Furthermore, if the locus S were to reduce to a curve, this curve could be represented parametrically by equations of the form (1.2). If in these equations the parameter t is set equal to any function of u, v, the result is three equations of the form (1.3), for which the jacobians J1 are easily proved, by actual calculation, to vanish identically. Conversely, the identical vanishing the jacobians J1 would imply that the locus of the point P was not a proper surface. For, if the jacobians all vanish identically, then the functions x, y, t are three solutions of a linear homogeneous partial differential equation of the form
a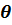 
u +b 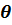v = 0 (1.5)
in which the coefficients a, b are functions of u, v. The theory of linear partial differential equations of the first order tells us how to integrate this equation. First form the associated ordinary differential equation
bdu-adv=0 (1.6)
This equation has an integral
t (u, v) = const (1.7)
and the most general solution of equation (1.5) is given by the formula
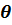u = F (t( u, v ), (1.8)
the function F being arbitrary. Consequently, the coordinates x, y, z are either all constant or are, at most functions of a single parameter t, so that either P is a fixed point or else has for its locus a curve.
Even if the jacobians J1, J2, J3 do not all vanish identically on the rectangle Т. It may happen that they vanish simultaneously for one or more isolated pairs of values of u, v or perhaps they vanish simultaneously along a curve v=v (u) in T. Any point of a real proper analytic surface at which the jacobians J1 J2, J3 vanish simultaneously is called singular, although the singularity may belong to the parametric representation being used for the surface defined as a point-locus, as in the case of the sphere, or else the singularity may belong to the surface itself. A surface, or portion of a surface, which is free of singular points may be called nonsingular.
Elimination of u, v from the parametric equations (1.3) of a surface S would lead to the implicit equation (1. 1) of S. Vice versa if the implicit equation (1.1) of a surface is desired, let two of the variables, say x and y, be arbitrary functions of two parameters u, v, and then solve (I.I) for z as a function of u, v. In particular, we might take z=u, y=v. Then solution of z would lead to the explicit equation (1.2) of the surface, except that u and v would occur in place of x and y, respectively. Indeed, the explicit equation (1.2) of a surface, when supplemented by the identities x=x, y=y, becomes the parametric equations
X=x, y=y, z=f(x, y)
of the same surface, the parameters now being the coordinates x, y.
Post-Reading Activity.
Ex. 7. Match the English words and word combinations with the Russian equivalents.
| 1. a double infinity of points 2. the locus of a point 3. two degrees of freedom 4. to impose a condition 5. a variable point 6. a missing variable 7. the resulting equation 8. a real proper analytic surface 9. with respect to 10. to vanish identically 11. to reserve the right 12. under suitable conditions 13. to reduce to a curve 14. a linear homogeneous partial differential equation 15. vice versa 16. arbitrary functions | a. тождественно обращаться в нуль b. две степени свободы c. геометрическое место точки d. сохранять право e. линейное однородное дифференциальное уравнение в частных производных f. двойная бесконечность точек g. отсутствующая переменная h. налагать условие i. полученное уравнение j. переменная точка k. сводиться к кривой l. при подходящих условиях m. наоборот, обратно n. произвольные функции o. действительная собственная аналитическая поверхность p. относительно |
Ex. 8. Find out whether the statements are true or false. Use introductory phrases.
| Exactly. Quite so. I fully agree to it. I don’t think this is the case. | Quite the contrary. Not quite. It’s unlikely. Just the reverse. |
1. To represent a surface analytically, we establish a polar coordinate system. 2. The equation f (x, y, z) = 0 is called an implicit equation of the surface. 3. The simplest surface of all types of surfaces is a cone. 4. In the parametric equations of the surface x = x (u, v); y = y (u, v); z =z (u, v) the letters x, y, z denote the parameters. 5. A surface or a portion of a surface, which is free of singular points may be called singular. 6. A surface is proper if it does not reduce to a curve. 7. If the equation f (x, y, z) = 0 is homogeneous in x, y, z, it represents a plane. 8. The explicit equation of the surface Z = f (x, y) is a special case of the implicit equation of the form F (x, y, z) = 0 if we transpose z to the right member.
Ex. 9. Translate the sentences, point out the meaning of the words.
| 1. order (n) 2. in order that in order to | 1. порядок, последовательность исправность, хорошее состояние, приказ, распоряжение 2. для того, чтобы |
1. The names in this list are placed in alphabetical order. 2. Get your ideas in some kind of order before beginning to write. 3. The device has been repaired and it is now in perfect order. 4. It is the business of the police to keep order. 5. He ordered that the work should be started at once. 6. Phone him in order that he should arrive in time. 7. In order to understand the procedures, consider the following analogy.
Ex. 10. Complete the sentences using the given word-groups:
| at the origin, the variables, the implicit equation of the surface, a plane, the parametric equations of the surface, arbitrary, a curve, singular, nonsingular, vanish simultaneously. |
1. The equation F (x, y, z) = 0is called … 2. If this equation is linear in the variables x, y, z, the surface which it represents is …, and if it is homogeneous in x, y, z, it represents a cone which vertex is … 3. A surface is proper if it does not reduce to … 4. The function F in the equation θ = F (t (u, v)) is… 5. Any point of a real proper analytic surface at which the jacobians … is called … 6. A surface, or a portion of a surface, which is free of singular points may be called …7. Equations x = x (u, v); y = y (u, v), z = z (u, v) are called …, whose parameters are …
Ex. 11. Complete the sentences using the right meaning of the word.
| 1. to mean (meant, meant) 2. means 3. mean 4. by no means 5. by means of | 1. (v) значить, предназначаться для, подразумевать под; 2. (n) средство; 3. (а) средний, (n) середина; 4. никоим образом 5. при помощи, посредством |
1. Your friendship … a great deal to me, I value it highly.
2. A dictionary tries to tell you what words …
3. What do you … by saying that? What have you in mind?
4. Is this figure … to be a 1 or a 7?
5. Does the end always justify the…?
6. Thoughts are expressed by … of words.
7. These results are by … satisfactory.
8. The … of 3, 5 and 7 is 5.
9. The happy or golden … is a moderate course of action.
Ex. 12. Translate the sentences from Russian into English, use the Subjunctive Mood.
1. Проверьте решение этой задачи, чтобы не получить неверный результат. 2. Он предложил, чтобы они рассмотрели многоугольники, т.к. этот тип геометрических фигур очень важен при изучении геометрии. 3. Жаль, что мы не исключили неизвестные, мы смогли бы решить эту систему уравнений. 4. Чтобы составить уравнение данной кривой, определим геометрическое место точек. 5. Пора ввести однопараметрическое семейство кривых на поверхности S. 6. Нам следует представить данные кривые аналитически с помощью системы уравнений. 7. Необходимо, чтобы часть поверхности не содержала особых точек. 8. Нам бы хотелось, чтобы в этом случае якобиан стремился к нулю. 9. Было бы лучше, если бы один из параметров менялся, в то время как другой оставался постоянным.
Ex .13. Answer the questions:
1. What does this text consider? 2. What must be established in order to represent a surface analytically? 3. What types of surfaces do you know? 4. A plane and a sphere are the simplest types of surfaces, aren’t they? 5. Is the equation F (x, y, z) = 0 an implicit or an explicit equation of a surface? 6. When does the equation F (x, y, z) = 0 represent a plane, a cone and a cylinder? 7. What can you say about the equation x = x (u, v); y = y (u, v);
z = z (u, v)? 8. What does it mean to say that a surface is proper? 9. What is a jacobian? 10. What do we call any point of a real proper analytic surface at which the jacobians vanish simultaneously? 11. What surface is called nonsingular?
Ex.14. Topics for discussion.
1. Speak on the definition of a surface given in this text and the definitions given in the lectures on differential geometry.
2. Discuss implicit and explicit equations of a surface.
3. Speak about the cases ,when a surface represented by the equations
x = x (u, v), y = y (u, v), z = z (u, v) reduces to a point or to a curve.
Ex. 15. Say it in English.
1. В этом тексте даётся определение поверхности и ее аналитическое представление. 2. Установим левостороннюю ортогональную декартову систему координат для того, чтобы представить поверхность аналитически. 3. Эта система координат имеет масштаб измерения для всех трех осей. 4. Затем мы налагаем одно условие на точку Р (x, y, z) уравнением вида F (x, y, z) = 0. 5. Это уравнение называется неявным уравнением поверхности. 6. Плоскость, сфера, цилиндр, конус известны как простые типы поверхностей. 7. Они могут быть представлены уравнением (x, y, z) = 0 при определенных условиях. 8. Уравнения х (u, v),y=y (u, v), z=z (u, v) с переменными v, u называются параметрическими уравнениями поверхности. 9. Любая точка поверхности, в которой якобианы одновременно равны нулю, называется вырожденной, а поверхность, не имеющая вырожденных точек, называется невырожденной. 10. Поверхность является собственной поверхностью, если она не превращается в кривую.
Ex. 16. Read the text and find the answers to the following questions.
1. What is a surface in mathematics? 2. Where does the concept of a surface find application? 3. What is a topological surface? 4. What is a coordinate chart? 5. What is known as the boundary of the surface?
TEXT B
Surface
In mathematics, specifically, in topology, a surfaceis a two-dimensional, topological manifold (множество, многообразие). The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball. On the other hand, there are surfaces, such as the Klein bottle, that cannot be embedded in three-dimensional Euclidean space without introducing singularities or self-intersections.
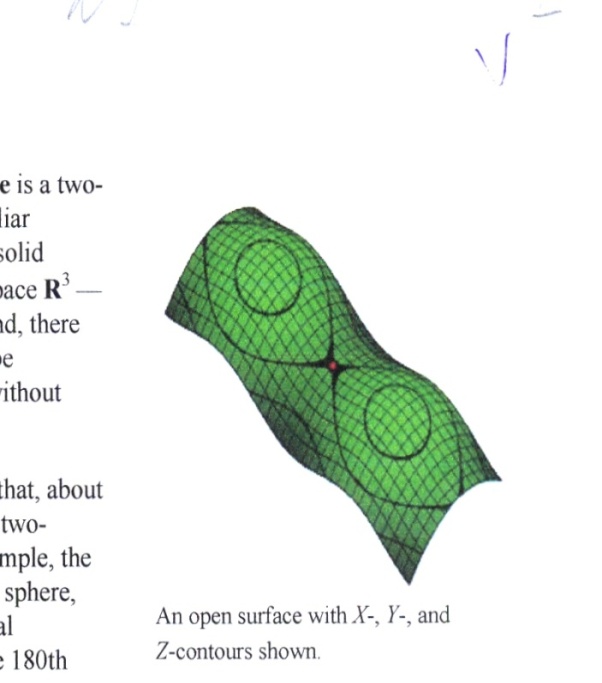To say that a surface is "two-dimensional" means that, about each point, there is a coordinate patch (часть)on which a two-dimensional coordinate system is defined. For example, the surface of the Earth is (ideally) a two-dimensional sphere, and latitude (широта) and longitude (долгота) provide two-dimensional coordinates on it (except at the poles and along the 180th meridian).
The concept of a surface finds application in physics, engineering, computer graphics, and many other disciplines, primarily in representing the surfaces of physical objects. For example, in analyzing the aerodynamic properties of an airplane, the central consideration is the flow of air along its surface.
A (topological) surface is a nonempty second countable Hausdorff topological space in which every point has an open neighbourhood (окрестность) homeomorphic to some open subset of the Euclidean plane E2. Such a neighborhood, together with the corresponding homeomorphism, is known as a (coordinate) chart (координатные сетки).It is through this chart that the neighborhood inherits (наследовать) the standard coordinates on the Euclidean plane. These coordinates are known as local coordinates and these homeomorphisms lead us to describe surfaces as being locally Euclidean.
More generally, a ('topological) surface with boundary is a Hausdorff topological space in which every point has an open neighbourhood homeomorphic to some open subset of the closure of the upper half-plane H2 in C. These homeomorphisms are also known as (coordinate) charts. The boundary of the upper half-plane is the x-axis. A point on the surface mapped via a chart to the x-axis is termed a boundary point. The collection of such points is known as the boundary of the surface which is necessarily a one-manifold, that is, the union of closed curves. On the other hand, a point mapped to above the x-axis is an interior point. The collection of interior points is the interior of the surface which is always non-empty. The closed disk is a simple example of a surface with boundary. The boundary of the disc is a circle.
The term surface used without qualification refers to surfaces without boundary. In particular, a surface with an empty boundary is a surface in the usual sense. A surface with an empty boundary which is compact is known as a 'closed' surface. The two-dimensional sphere, the two-dimensional torus (тор), and the real projective plane are examples of closed surfaces.