Guess the meaning of the followed words.

UNIT I

Grammar: The Participle. Its forms and functions.

	ACTIVE	PASSIVE
PARTICIPLE I	expressing	being expressed
PERFECT PARTICIPLE	having expressed	having been expressed
PARTICIPLE II	-	expressed

Ex. 1. Read and translate the following sentences in which

a) Participle I Active is used as anAttribute:

1. The line passing through these two points is a diameter. 2. The scientist working at this method is well known. 3. Maths is a science requiring professionals, not amateurs. 4. Yesterday the President of the company received an e-mail informing him about the arrival of his business partners.

5. Most mathematicians are men of genius having extraordinary mental abilities.

b) Participle I Passive is used as an Attribute:

1. The examples being given justify what has already been proved. 2. The solution of the problem being considered can be expressed in other ways. 3. The methods being applied seem rather complicated. 4. The quantity being defined is related to the volume of this container. 5. The device being used in our laboratory should be improved.

c) Participle II is used as an Attribute:

1. A number written in front of an algebraic expression is a coefficient. 2. A dot placed between any two numbers is sometimes used as a sign of multiplication. 3. Some questions asked by the teacher are to be stated more precisely. 4. The results so far received do not satisfy us. 5. The methods used in solving the problem were the same.

d) Participle I (Active, Passive) is used as an Adverbial Modifier:

1. Being close to the solution of the problem, he published the results received. 2 When using mathematical language, we avoid vagueness and unwanted extra meanings of our statements. 3. Being spread throughout the world, the Internet provides the connection of networks to enable computers and software to communicate. 4. While considering the group concept, the students must remember four axioms. 5. Being reduced the fraction does not change its value.

e) Participle II is used as an Adverbial Modifier:

1. Expressed in terms of symbols, these relations produce a formula. 2. When used as scientific terms, these concepts have different meanings. 3. If designed and devised in a proper way, the symbolic language becomes universal. 4. When given the information, they were able to complete the research. 5. When asked about the measure of the circumference, the pupil could not say anything.

f) Perfect Participle (Active, Passive) is used as an Adverbial Modifier:

1. Having obtained the necessary devices, we could finish our experiment.

2. Having become familiar with the main laws of statics, we can study the laws of dynamics. 3. Having made a lot of experiments, Faraday discovered the electromagnetic induction. 4. Having picked out the product corresponding to these tables, we obtained a coordinate system for the space. 5. Having been properly approached, the problem appeared easy to solve. 6. Having been invited to the conference, the scientist started preparing his plenary report.

Ex. 2. Translate the following into Russian. Pay attention to the difference in translating Participle I and II in the function of an Attribute. Keep in mind several meanings of the verb “to follow”.

		следовать за кем-либо, чем-либо
	to follow	следить за кем-либо, чем-либо
		придерживаться чего-либо

Model: The film following the report showed… Фильм, последовавший за докладом, показал…	Model:Thefilm followedby a discussion showed… Фильм, за которым последовала дискуссия, показал…
1. The concert following the meeting showed…	1. The experiment followed by a lecture showed…
2. The discussion following the report demonstrated…	2. His research work followed by an article demonstrated…
3. The statement of President following the events in the country was…	3. The theory followed by our professor was…
4. A number of works following the experiments proved…	4. The method followed by us proved…
5. The lecture following the demonstration of the experiment was…	5. The lecture followed by a demonstration of a film was…

Ex. 3. Answer the following questions using the model.

Model 1: Sp. They used some new method of definition. Did it give good results?

St. Yes, the method used gave good results.

1. They made some measurements. Are the measurements accurate?

2. They received good results. Do these results satisfy them?

3. They demonstrated some experiments. Do these experiments relate to your work?

4. He has measured the volume of the container. Is the volume very large?

5. You have found this relation. Does it remain constant under ordinary conditions?

6. You have determined the length of this line segment. Does this length equal 10 centimeters?

Model 2: Sp. He works at the Bureau of Standards. Does he deal with the units of measurement there?

St.You are right. Working at the Bureau of Standards, he deals with the units of measurements.

1. They follow that new method. Will they achieve good results?

2. We know length and time. Can we define velocity?

3. You were interested in these results. Did you discuss them?

4. The experiment was very important. Was it made accurately?

Model 3: Sp. Now, you have found the relation between these three lengths. Can you define the volume?

St. Yes, having found this relation, we can define the volume.

1. Now, you have found the length in meters. Can you convert it into English yards?

2. They have just tested the new equipment. Will they put it into operation?

3. They have just measured the area. Can they show us the results?

4. They have calculated the sum of the areas of the two smaller squares. Will they find the area of the largest square?

Ex. 4. Match the left and the right parts of the sentences.

1. Geometry is a branch of mathematics	a) formed of successive sections or segments of straight lines.
2. A sequence is a succession of quantities	b) accepted without any proof.
3. A chord is a line segment	c) extending indefinitely in all directions.
4. A matrix is a set of quantities	d) investigating the relations, properties and measurements of solids, surfaces, lines and angles.
5. A broken line is a line	e) arranged in rows and columns to form a rectangular array.
6. A plane is a flat surface	f) joining any two points on the circumference of a circle.
7. Axioms are the facts	g) formed according to some fixed law.

Ex. 5. Complete each of the sentences below by choosing one of the Participles given in parentheses.

1. An algebraic expression is one in which several numbers …(representing, represented, having been represented) are connected by signs …(being indicated, indicated, indicating) the operations and their order.

2. … (Defining, Having defined, Being defined) the first and the second lengths, we may find the area.

3. We explained the binary system … (being given, giving, having been given) a specific example.

4. We can always get a closer approximation … (adding, added, having been added) digits at the right.

5. Unless otherwise … (stating, stated, being stated), the values used are taken in the decimal system.

6. No number exists which has a negative value when … (multiplied, multiplying, having been multiplied) by itself.

7. … (Leaving, Having left, Being left) alone, they kept silence for some time and didn’t know what to speak about.

8. Maths is a device … (designing, having designed, designed) to enlarge human power.

Ex. 6. Mixed Bag. State the forms and functions of Participles in the following sentences and translate them.

1. Discussing some interesting problems, they didn’t notice when somebody came in.

2. Being interested in mathematics, Tom spends more time on it than on any other subject.

3. Having informed her before, I was sure that she was waiting for me.

4. Don’t forget to put the lights out when going to bed.

5. Being given two more days, the student could complete his term paper.

6. Having been considerably improved, the device was widely used in research.

7. When asked about his experiments, the scientist refused to give any details.

8. The substance obtained was thoroughly investigated.

9. The phenomenon was rather complicated and the processes involved are not yet clear.

10. A graph is given showing the dependence of pressure on temperature.

11. When crossing the street, first look left and then right.

12. The method followed by Professor Webster A.G. was accurate.

Ex. 7. Translate the following sentences into English using the necessary Participles.

1. Собрав весь необходимый материал, студент смог хорошо написать курсовую работу. 2. Не зная, как перевести это предложение, я попросил моего друга помочь мне. 3. Тщательно изучив всю информацию, ученый ответил на все поставленные вопросы. 4. Машина, которая следовала за нами, была зеленого цвета. 5. Деревья, растущие перед нашим домом, были посажены моим дедом. 6. Язык, на котором говорят в США, называется американским вариантом английского языка. 7. Участники конференции заслушали пленарный доклад, за которым последовало много вопросов. 8. Повернув направо, мы увидели новое здание с большими окнами. 9. Будучи очень рассеянным, он сделал много ошибок, переписывая текст. 10. Взглянув на него с удивлением, она вышла из комнаты, не сказав ни слова. 11. Зная английский хорошо, он сделал прекрасный доклад на конференции. 12. Проблема, которую он затронул в своем докладе, заслуживает внимания.

Pre-Reading Activity

TEXT A

GROUP THEORY

The theory of groups, a central concern of contemporary maths, has evolved through a progression of abstractions. A group is one of the simplest and the most important algebraic structures of consequence.

Some of the components of the group concept (i.e., those essential properties that were later abstracted and formulated as axioms) were recognized as early as 1650 B.C. when the Egyptians showed a curious awareness that something was involved in assuming that ab=ba. The Egyptians also freely used the distributive law, namely, a(b+c)=ab+ac.

The group concept was not recognized as explicitly as were some of its axioms, but even so it was implicitly sensed and used before Abel and Galois brought it into focus and before Cayley (1854) defined a general abstract group.

A group in its most abstract form consists of a number of entities known as the elements of a group which can be combined together according tovarious axioms. The form of combination is one in which two elements combine together to give a unique third element. This generalizes the familar operations of addition in which two numbers are added toform a third number or of multiplication in which they are multiplied to give their product. For convenience, this abstract operation is called multiplication and denoted by writing the elements close together. The order in which the elements are written is usually important.

The general definition of a group. A collection of elements, G, will be called a groupif its elements А, В, С... can be combined together (multiplied) in a way which satisfies the four axioms:

I. Closure.The product of any two elements of the group is a unique element which also belongs to the group.

II. Associative. When three or more elements are multiplied, the order of the multiplications makes no difference, i. e.

A(BC) = (AB)C=ABC.

III. Identity. Among the elements there is an identity element denoted

by I, with the property of leaving the elements unchanged on multiplication, i. e.

AI = IA = A.

IV. Inverses. Each element, A, in the group has an inverse (or reciprocal)

A^-1such that AA^-1=A^-1 A = I.

A group does not need to have an infinite number of elements, the four elements 1, i, -1, -iform a finite group under multiplication. Neither does it need to use ordinary multiplication as the formcombination. The positive and negative integers form a group with addition as the law of combination, the number 0 as the identity and a change of sign to denote the inverse.

Subgroups. When a number of elements selected from a group do themselves form a group it is known as a subgroup. The identity element for the group is also the identity element for the subgroup. The closure and existence of inverses are, therefore, the only laws that need to be verified individually. Every group has at least one subgroup, namely, the minor one consisting of the identity element alone.

Post-Reading Activity

Ex. 8. Answer the following questions.

1. What is the central concern of contemporary maths? 2. Where can we find the traces of the components of the group concept? 3. Who was the first to bring the notion of a group concept info focus? 4. When and by whom was the definition of a general abstract group given? 5. What is a group? 6. According to what axioms can the elements of a group be combined? 7. The order in which the elements are written is not important, is it? 8. What is the main property of an identity element? 9. How many elements may a group have? 10. What is a subgroup? 11. What is the minor subgroup of a group?

Ex. 9. Match the English words and word combinations with the Russian equivalents.

1. a curious awareness	a. принадлежать группе
2. a group concert	b. конечная группа
3. to sense implicitly	c. проверить закон
4. a number of entities	d. ряд (некоторое количество) объектов
5. a unique element	e. современная математика
6. to belong to a group	f. понятие группы
7. an identity element	g. удивительная осведомленность
8. a finite group	h. это не имеет значения
9. to verify a law	i. неявно осознавать
10. an infinite number of elements	j. неограниченное количество элементов
11. the contemporary maths	k. однозначный элемент
12. it makes no difference	l. единичный элемент

Ex. 10. Find out whether the statements are True or False. Use the introductory phrases:

TEXT B

UNIT II

Pre-Reading Activity

Guess the meaning of the following words:

collection (n) [kq'lekSqn] algebra (n) ['xlGIbrq]

object (n) ['ObGIkt] phrase (n) ['freIz]

element (n) ['elImqnt] symbol (n) ['sImbql]

theory (n) ['TIqrI] standard (a) ['stxndqd]

concrete (a) ['kOnkrJt] season (n) ['sJzqn]

real (a) ['rIql] variation (n) [vFrI'eISqn]

interest (n) ['IntrIst] idea (n) [aI'dIq]

abstract (a) ['xbstrqkt] vertical (a) ['vWtIkql]

sphere (n) ['sfIq] fact (n) ['fxkt]

special (a) ['speSql] mathematics (n) [mxTI'mxtIks]

TEXT A

SETS

A set is a collection of objects. The objects belonging to the set are the elements or members of the set. Although in introducing set theory it is helpful to work with concrete sets, whose members are real objects, the sets of interest in mathematics always have members which are abstract mathematical objects: the set of all circles in the plane, the set of points on a sphere, the set of all numbers.

As in ordinary algebra we shall use letters to represent sets and elements, small letters being used for elements and capital letters for sets. But it is impossible to keep rigidly to this convention because sets can themselves be elements of other sets. The phrase “is a member of” occurs so often that it is convenient to have a symbol, the one currently in use is 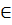Guess the meaning of the followed words. - student2.ru . So x 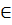S means “x is a member of S”.

A set is considered to be known if we know what its elements are – or at any rate if in theory we can find out. There are many ways of specifying a set, of which the simplest is to list all the members. The standard notation for this is to enclose the list in curly brackets. So {1, 2, 3, 4} is the set whose members are 1, 2, 3, 4 and only these, while {spring, summer, autumn, winter} is the set of seasons.

Two sets are equal if they have the same elements. We can easily write things like {1, 2, 3, 4, 4}. Despite being mentioned several times, there is only one 4 in the set, which being thus equal to {1, 2, 3, 4}. When using the curly bracket notation, elements listed more than once are thought of as occurring once in the set. The order inside the brackets makes no difference. The set {1, 2, 3, 4, 4} has the same elements as {1, 2, 3, 4}, so is the same set.

More generally, a symbol such as {all epic poems} denotes the set of all epic poems. A variation of this idea allows us to write {x|x is an epic poem} for the same set. The vertical bar may be read as “such that”, and the set of all x such that x is an epic poem is the same as the set of all epic poems. The set

{n|n is an integer and 1 ≤ n ≤ 4} is the same as the set {1, 2, 3, 4}.

Instead of a list, we give a property which specifies precisely the elements we wish to be included in the set. If we are careful with our definitions, making sure that we specify the exact property we want, this is as good as a list, and is usually more convenient. For sets with infinitely many members, such as

{all whole numbers}, it is in any case impossible to give a complete list. The same is true for sets with a sufficiently large finite set of elements.

The mathematical notion of a set allows sets with only one member or even no members at all. If you specify a set by some property it may turn out later that there is only one object with that property or none at all. Sets with one element must not be confused with the element itself. It is not true that x and {x} are equal; {x} has just one member, namely x, while x may have any number of members depending on whether or not it is a set, and if it is, which set.

For exactly the same reasons that we allow sets with just one element, we have to allow sets with no elements at all. A set with no elements is called an empty set. A fact now emerges which many people find surprising: there is only one empty set. All empty sets are equal. Any two empty sets are equal because, in the absence of any members to distinguish them by, there is no way to tell them apart. Having established that there is just one empty set we can give it a symbol, the current one being Ø (which is a special symbol). The empty set is not “nothing” …, nor does it fail to exist. It is just as much in existence as any other set. It is its members that do not exist. It must not be confused with the number 0: for 0 is a number, whereas Ø is a set. Ø is one of the most useful sets in mathematics. One of its uses is to express concisely that something does not happen.

Post-Reading Activity.

Ex. 7. Answer the following questions:

1. What is a set? 2. What are the elements of the set? 3. What sets are of interest in mathematics? 4. What do we use to represent sets and elements? 5. What set is considered to be known? 6. What is the simplest way of specifying a set? 7. What is the standard notation for a set? 8. What sets are equal? 9. How can we specify the elements of a set? 10. How many members may a set have? 11. What is an empty set? 12. How is an empty set represented? 13. Does an empty set exist at all?

Ex. 8. Match the English words and word combinations with the Russian equivalents.

1. exact property; 2. to enclose the list in curly brackets; 3. to keep rigidly to the convention; 4. set theory; 5. just one element; 6. a finite set of elements; 7. elements listed; 8. concrete sets; 9. a way of specifying a set; 10. the same elements; 11. infinitely many elements; 12. standard notation; 13. abstract objects; 14. a complete list; 15. it makes no difference; 16. the sets of interest in mathematics; 17. members of the set.

a. члены множества; b. множества, вызывающие интерес в математике; c. конкретные множества; d. абстрактные объекты; e. способ определять множество; f. обычно принятое обозначение; g. заключить перечень в фигурные скобки; h. одни и те же элементы; i. перечисленные элементы; j. точное свойство; k. бесконечное число элементов; l. полный перечень; m. конечное число элементов; n. только один элемент; o. не имеет значения; p. теория множества; q. строго придерживаться условия.

Ex. 9. Fill in the blanks with the words from the box.

empty, members, to list, notation, specifying, difference, precisely, the same

1. The objects belonging to the set are the elements or … of the set. 2. There are many ways of … a set. 3. The simplest way of specifying a set is … all the members. 4. The standard … is to enclose the list in curly brackets. 5. Two sets are equal if they have … elements. 6. The order inside the brackets makes no … 7. Instead of a list, we give a property which specifies … the elements. 8. A set with no elements is called an … set.

Ex. 10. Ask questions for which the given sentences are answers.

1. A set is a collection of objects. (What?) 2. The objects belonging to the set are the elements or members of the set. (Which?) 3. The sets of interest in mathematics always have members which are abstract mathematical objects. (What?) 4. In the algebra of sets we use letters to represent sets and elements. (Where?) 5. A set is considered to be known if we know what its elements are. (When?) 6. There are many ways of specifying a set. (How many?) 7. The standard notation is to enclose the list in curly brackets. (What?) 8. Two sets are equal if they have the same elements. (When?) 9. Instead of a list, we give a property which specifies precisely the elements of the set. (What?) 10. For sets with infinitely many members, it is impossible to give a complete list. (Which?) 11. The mathematical notion of a set allows sets with only one member or even no members at all. (What?) 12. A set with no elements is called an empty set. (What?) 13. All empty sets are equal. (What?)

Ex. 11. Find out whether the statements are true or false. Use introductory phrases.

TEXT B

SET THEORY

Set theory is the branch of mathematical logic that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics. The language of set theory can be used in the definitions of nearly all mathematical objects.

The modern study of set theory was initiated by George Cantor and Richard Dedekind in the 1870s.

Set theory begins with a fundamental binary relation between an object o and a set A. If o is a member (or an element) of A, write o ∈ A. Since sets are objects, the membership relation can relate sets as well.

A derived binary relation between two sets is the subset relation, also called set inclusion. If all the members of set A are also members of set B, then A is a subset of B, denoted A ⊆ B. For example, {1,2} is a subset of {1,2,3} , but {1,4} is not. From this definition, it is clear that a set is a subset of itself; for cases where one wishes to rule out this, the term ‘proper subset’ is defined. A is called a proper subset of B if and only if A is a subset of B, but B is not a subset of A.

Just as arithmetic features binary operations on numbers, set theory features binary operations on sets.

Set theory as a foundation for mathematical analysis, topology, abstract algebra, and discrete mathematics is likewise uncontroversial; mathematicians accept that (in principle) theorems in these areas can be derived from the relevant definitions and the axioms of set theory. Few full derivations of complex mathematical theorems from set theory have been formally verified, however, because such formal derivations are often much longer than the natural language proofs mathematicians commonly present.

Set theory is a major area of research in mathematics, with many interrelated subfields.

UNIT III

Grammar: THE GERUND. ITS FORMS AND FUNCTIONS.

FORMS OF THE GERUND

	INDEFINITE	PERFECT
ACTIVE	asking writing	having asked having written
PASSIVE	being asked being written	having been asked having been written

Ex. 1. Study the functions of the Gerund. State their forms. Translate the sentences into Russian.

a) the Gerund is used as a Subject.

1. Writing a sentence in algebraic form, as we have seen, involves two steps. 2. Drawing a straight line in one direction gives you a one way extension. 3. Reducing a fraction means bringing it to lower terms. 4. Reading slowly is useful for beginners. 5. Locating the point on the y-axis gives you the first point on the line. 6. Knowing the properties of equality will help you decide whether a sentence is true or false.

b) the Gerund is used as a part of a Predicate.

1. Our task is proving the correctness of the given statement. 2. The young scientist began experimenting. 3. We expected being given further assistance. 4. This terminology needs improving. 5. The scientist expected being included in the experimental group. 6. She stopped investigating the problem as her approach was wrong.

c) the Gerund is used as a Direct object.

1. We discussed improving the shape of the model. 2. Do you mind being examined first? 3. I don’t remember speaking to him about this fact. 4. Avoid making such bad mistakes. 5. They are busy now reading the text. 6. He suggested taking part in this conference.

d) the Gerund is used as a Prepositional object.

1. He was prevented from finishing his work. 2. We succeeded in accomplishing our task. 3. He insisted on writing the thesis as soon as possible. 4. These computers are capable of solving systems with a hundred or more unknowns, if necessary. 5. They are concerned with applying their knowledge of the subject to solving these problems. 6. We cannot agree to testing the new method without being given additional time.

e) the Gerund is used as an Attribute.

1. What ways of learning words do you find most effective? 2. This is the method of doing such tasks. 3. I can’t improve my English because I don’t have any opportunities of speaking it. 4. The idea of using symbols instead of words proved very helpful. 5. There exists a very efficient algorithm for solving most linear programming problems. 6. The procedure of reducing a fraction to its lowest terms is not complicated.

f) the Gerund is used as an Adverbial modifier.

1. In considering the problem we have to deal with the laws of motion. 2. The product may be found by multiplying the factors contained in the given mathematical sentence. 3. We can’t agree to testing the new method without being given additional time. 4. In naming geometric objects we often use capital letters. 5. By applying the knowledge of geometry you can locate the point in the plane. 6. After discussing the problem in detail they found the best solution.

Ex. 2. State the form and the function of the Gerund. Translate the sentences into Russian.

1. We insisted on carrying out another experiment to check the results.

2. The absolutely new contribution made by Descartes was in importing the idea of motion into geometry.

3. This is the basic method of solving problems of statics.

4. It is worth noting that the work of the early Arab mathematicians makes no clear division between arithmetic and algebra.

5. Since the equation is linear and has constant coefficients it can be easily solved by using classical differential equation theory.

6. He also improved the notation for representing the extraction of roots.

7. Combining the integrals gives the following equation.

8. The preceding definitions have laid the foundation for considering the variation of a functional.

9. Leonardo’s solution is worth quoting for its elegance.

Ex. 3. Put the Gerund in the correct form. Use prepositions where necessary.

1. She continued (to translate) the text from English into Russian.

2. He found the product (to multiply) the numerals.

3. She is afraid (to take) the exam.

4. He used a ruler (to draw) a straight line.

5. One must be very careful (to measure) the volume of an object.

6. They insist on the question (to reconsider).

7. She stopped (to investigate) the problem as her approach was wrong.

8. The problem (to discuss) various points of view was a very useful exercise.

9. Measurement is a process (to associate) numbers with certain objects.

Ex. 4. Insert prepositions (in, of, to, from, by). You can use the same preposition in more than one sentence.

1. His mathematical power, which never failed him to the end of his life, was employed at this period __ originating the calculus of probabilities, and __ inventing the arithmetical triangle.

2. The mathematician who came nearest __ solving the challenge questions issued by Pascal on the cycloid (циклоид) was John Wallis.

3. But he differs from B. F. Cavalieri (an Italian mathematician) __ regarding lines as made up of infinitely small lines, surfaces of infinitely small surfaces, and volumes of infinitely small volumes.

4. Leonardo’s favorite method __ solving many problems is by the method of ‘false assumption’, which consists __ assuming a solution and then altering (изменение) it by simple proportion as in the rule of three (вычислительный метод в математике).

5. We have succeeded __ verifying that the increment (приращение) can be written in the form of the following equation.

6. His famous experiment __ dropping bodies of different weights from the tower of Pisa enabled him to demonstrate that all bodies undergo the same acceleration __ falling towards the earth, a result which his experiment with light and heavy pendulums (маятники) also proved.

7. He also discusses solids generated __ revolving a curve about an axis, and in the last section deals with the problems of maxima and minima.

8. The intellectual trend of that time was such as to prevent mathematics __ becoming a popular subject.

9. Since Euler’s equations usually cannot be solved analytically, one naturally thinks __ using numerical integration.

10. F. Viet (a French mathematician) succeeded __ finding 23 of the 45 roots.

Ex. 5. Change the time clause into the ‘in + Gerund’ structure.

Model: He made a mistake when he was proving the theorem.

Pre-Reading Activity

Guess the meaning of the following words:

differential adj. [dIfq'renSql] original adj. [O'rIGqnl]

general adj. ['Genqrql] primitive adj. ['prImItIv]

constant adj. ['kOnstqnt] integration n. [IntI'greISqn]

algebraical adj. [xlGI'breIkql] theoretical adj. [TIq'retIkql]

transcendental adj. [trxnsen'dentl] theorem n. ['TIqrqm]

coefficient n. [kouI'fISqnt] unique adj. [ju:'ni:k]

classify v. ['klxsIfaI] initial adj. [I'nISql]

linear adj. ['lInIq] integrable adj. [In'tIgrqbl]

rationalize v. ['rxSnqlaIz] integral adj. ['IntIgrql]

total adj. [toutl]

TEXT A

Post-Reading Activity

Ex. 11. Answer the following questions.

1. When was the term “differential equation” first used? 2. What did this term denote at that time? 3. What does this term denote now? 4. In what ways are differential equations classified? 5. What kinds of differential equations do you know? 6. What does an ordinary differential equation express? 7. What does a partial differential equation involve? 8. What does a total differential equation contain? 9. What is the order of a differential equation? 10. What is the degree of a differential equation? 11. When is an ordinary or a partial differential equation linear? 12. What does the most general solution of an ordinary equation of order n involve?

Ex. 12. Match the English words and word combinations with the Russian equivalents.

1. an ordinary differential equation, 2. a partial differential equation, 3. a total differential equation, 4. an auxiliary variable, 5. a primitive, 6. differentiability and continuity, 7. point of view, 8. an existence theorem, 9. arbitrary constants, 10. simultaneously, 11. the first integral of the equation, 12. a step-by-step process, 13. differential coefficients, 14. apart from.

a. дифференцируемость и непрерывность; b. произвольные константы; c. обыкновенное дифференциальное уравнение; d. точка зрения; e. одновременно; f. дифференциальное уравнение в частных производных; g. первый интеграл уравнения; h. теорема существования; i. уравнение в полных дифференциалах; j. кроме, не говоря о, не считая; k. поэтапный процесс; l. вспомогательная переменная; m. дифференциальные коэффициенты; первообразная.

Ex. 13. Translate the following sentences into Russian.

1. Differential equations are now understood to include any algebraical or transcendental equalities which involve either differentials or differential coefficients. 2. When an equation is polynomial in all the differential coefficients involved, the power to which the highest differential coefficient is raised is known as the degree of the equation. 3. The coefficients of the linear equation are either constants or functions of the independent variable or variables. 4. In the formation of a differential equation from a given primitive it is necessary to assume certain conditions of differentiability and continuity of derivatives. 5. From this theorem, it follows that the most general solution of an ordinary equation of order n involves n, and only n, arbitrary constants. 6. Let the primitive be solved for c and this value of c be substituted into the derived equation. 7. When the given equation is of order n, and by a process of integration an equation of order Guess the meaning of the followed words. - student2.ru involving an arbitrary constant is obtained, the latter is known as the first integral of the given equation. 8. To make this point clear, let us consider, for instance, the differential equation of the following form c² + 2cy + a² - x² = 0.

Ex. 14. Find out whether the statements are true or false. Use introductory phrases.

TEXT B

UNIT IV

The Forms of the Infinitive

	Active	Passive
Indefinite	to translate	to be translated	Выражает действие одновременное с действием глагола сказуемого
Continuous	to be translating		Выражает одновременное длительное действие
Perfect	to have translated	to have been translated	Выражает действие предшествующее действию глагола сказуемого (переводиться прошедшим временем)
Perfect Continuous	to have been translating		Выражает предшествующее длительное действие

Pre-Reading Activity.

Reading Activity

TEXT A

EQUATION AND LOCUS

Two fundamental problems of analytic geometry. In this chapter we shall make a preliminary study of the following two fundamental problems of analytic geometry:

I. Given an equation, to determine its geometric interpretation or representation.

II. Given a geometric figure or condition, to determine its equation or analytic representation.

The students will note that these problems are essentially converses of each other. Strictly speaking, however, both problems are so closely related that together they constitute the fundamental problem of all analytic geometry. For example, we shall see later that, after obtaining the equation for a given geometric condition, it is often possible by a study of this equation to determine further geometric characteristics and properties for the given condition. Our purpose in initially considering two separate problems is not one of necessity, but rather one of convenience; we are thus enabled to focus our attention on fewer ideas at a time.

First Fundamental Problem. The Locus of an Equation.

Assume that we are given an equation in the two variables x and y, which we may write briefly in the form

f (x, y) =0(1)

In general there are infinitely many pairs of values of x and y which satisfy this equation. Each such pair of real values will be taken as the coordinates

(x, y) of a point in the plane.

This convention is the basis of Definition 1. The totality of points, and only those points, whose coordinates satisfy an equation (1), is called the locus or graph of the equation.

Another convenient expression is given by Definition 2. Any point whose coordinates satisfy an equation (1) is said to lie on the locus of the equation.

It cannot be emphasized too strongly that only those points whose coordinates satisfy an equation lie on its locus. That is, if the coordinates of a point satisfy an equation, that point lies on the locus of the equation; and conversely, if a point lies on the locus of an equation, its coordinates satisfy the equation. Since the coordinates of the point of a locus are restricted by its equation, such points will in general be located in positions which, taken together, form a definite path called a curve as well as a graph or locus.

Second fundamental problem. We will now consider the second fundamental problem of analytic geometry.

A geometric figure, such as a curve, is generally given by its definition. By the definition of an object is meant a description of that object of such a nature that it is possible to identify it definitely among all other objects of its class. The implication of this statement should be carefully noted: it expresses a necessary and sufficient condition for the existence of the object defined. Thus, let us consider that we are defining a plane curve of type C by means of a unique property P which C possesses. Then, in the entire class of all plane curves, a curve is of type C if and only if it possesses property P.

As a specific example, let us consider that familiar plane curve, the circle. We define a circle as a plane curve possessing the unique property P that all its points are equally distant from a fixed point in its plane. This means that every circle has property P; and conversely, every plane curve having property P is a circle.

For a curve, a geometric condition is a law which the curve must obey. This means that every point on the curve must satisfy the particular law for the curve. Accordingly a curve is often defined as the locus or path traced by a point moving in accordance with a specified law. Thus, a circle may be defined as the locus moving in a plane so that it is always at a constant distance from a fixed point in that plane. A locus need not necessarily satisfy a single condition; it may satisfy two or more conditions. Thus, we may have a curve which is the locus of a point moving so that it passes through a given point, and it is always at a constant distance from a given line. We may then summarize the preceding remarks in the followingdefinition:

A curve is the locus of all those points, and only those points, which satisfy one or more given geometric conditions.

The student should note that this definition implies that the given condition or conditions are both necessary and sufficient for the existence of the curve.

Post-Reading Activity.

Ex. 8. Answer the following questions:

1. What are the two fundamental problems of analytic geometry? 2. How many pairs of values of x and y satisfy the equation F(x, y) = 0? 3. What is the locus or graph of the equation? 4. What point lies on the locus of the equation F(x, y) = 0? 5. What are the coordinates of the point of a locus restricted by? 6. By what is a geometric figure generally given? 7. How may a circle be defined? 8. How many conditions may a locus satisfy? 9. What is the difference between the first and the second problems?

Ex. 9. Match the English words and word combinations with their Russian equivalents.

1. a familiar plane curve	a. совокупность точек
2. to lie on the locus	b. весь класс
3. strictly speaking	c. как необходимые, так и достаточные условия
4. two fundamental problems	d. известная плоская кривая
5. to write briefly	e. обязательно удовлетворять
6. the totality of points	f. точно говоря
7. the implication of a statement	g. единственное условие
8. both necessary and sufficient conditions	h. предварительное изучение
9. a preliminary study	i. тесно связанный
10. necessarily satisfy	j. находиться на графике
11. the entire class	k. записывать кратко
12. a single condition	l. две основные задачи
13. to pass through a given point	m. проходить через данную точку
14. closely related	n. смысл утверждения

Ex. 10. Give the corresponding plural forms of the following nouns.

a) us [əs] → i [aI] focus → foci

Calculus, genius, locus, modulus, nucleus, radius.

b) is [Is] → es [I:z] axis → axes

Thesis, emphasis, analysis, basis, hypothesis, crisis, phasis, parenthesis.

c) ix [Iks] → es [I:z] matrix → matrices

ex [əks] → es [I:z] vertex → vertices

Directrix, bisectrix, index.

d) on [ɔn] → a[ə] polyhedron → polyhedra

um [əm] → a [ə] datum → data

Continuum, medium, spectrum, minimum, maximum, phenomenon, criterion.

e) a [ə] → ae [i:] formula → formulae (formulas)

Abscissa, hyperbola, lacuna, corona.

Ex. 11. Use the plural and singular forms of the nouns given in Ex.10. The first letters of the words are given.

1. The area of an ellipse equals π times the product of the long and the short r… 2. If a curve is symmetric with respect to both a …, is it symmetric with respect to the origin? 3. Analytic methods give us a means of finding the equations of l… 4. The notion of a four-dimensional geometry is a very helpful one in studying physical p… 5. Find the equation of the ellipse with f … at the points (0, 4). 6. In each of the following h…, locate the vertices and f… 7. All these facts may serve as reference d… 8. C … is a branch of mathematics divided into two parts differential calculus and mathematical calculus. 9. Circular area is measured by its r… 10. Einstein was a mathematical g…

Ex. 12. Ask disjunctive questions ( tag-questions).

1. To draw the graph of a function isn’t difficult,...? 2. Don’t try to obtain the equation of a locus quickly, ...? 3. Every student must understand the implication of the equation of a locus,...? 4. Let’s do a preliminary study of the function,...? 5. This theorem constitutes a common property of fields,...? 6. For convenience we had to focus attention on the characteristic of the locus,...? 7. They have studied the entire class of plane curves, ...? 8. You should know the coordinates of a point to determine its position in a plane,...? 9. There is an analytic interpretation of the equation of a locus,...? 10. I’m to study the course of analytic geometry,...?

Ex. 13. Find out whether the statements are true or false. Use introductory phrases.

Exactly. Quite so. I fully agree to it. I don’t think this is the case.

Quite the contrary. Not quite. It’s unlikely. Just the reverse.

1. There exists a close relationship between two fundamental problems of analytic geometry.

2. After obtaining the equation for a given geometric condition it is impossible to determine further geometric properties for the given condition.

3. There is only one pair of values x and y satisfying the equation F(x, y)=0.

4. The totality of points satisfying Equation (1) is called the locus or graph of the equation.

5. Any point whose coordinates satisfy Equation (1) is said not to lie on the locus of the equation.

6. A geometric figure, such as a curve is generally given by its formula.

7. A circle possesses a unique property that all its points are equally distant from the points in its plane.

8. For the curve, a geometric condition is a law which the curve must obey.

9. A curve is the locus of the points which satisfy one and only one condition.

10. There is some difference between the first and the second problems of analytic geometry.

Ex. 14. Say these sentences in English.

1. Нам предстоит рассмотреть методы анализа линейных уравнений.

2. Во многих текстах чертёж уравнения называется кривой, даже если это прямая линия.

3. Такая кривая называется геометрическим местом точек уравнения.

4. Геометрическим местом точек уравнения (его графиком) является кривая, содержащая точки и только те точки, координаты которых удовлетворяют этому уравнению.

5. Иногда кривая может быть определена множеством условий, а не уравнением, хотя уравнение может быть получено из данных условий.

6. В этом случае рассматриваемая кривая являлась бы графиком всех точек на плоскости, которые соответствовали бы этим уравнениям.

7. Например, можно сказать, что кривая – это геометрическое место всех точек на плоскости, расположенных на фиксированном расстоянии от одной фиксированной точки, называемой центром окружности.

8. Прямая линия может быть определена как геометрическое место всех точек на плоскости, равноудалённых от двух фиксированных точек.

9. Метод выражения множества условий в аналитической форме даёт уравнения.

10. Основные понятия геометрического места точки в геометрии тесно связаны с понятием уравнения в алгебре.

Ex.15. Read and translate the following sentences. Group them according to the models.

Models.a) He should help us. (obligation). Он должен нам помочь.

b) You should have helped us. Вам следовало бы нам помочь.

(negative probabilities; unwanted things).

c) We answered that we should help him. Мы ответили, что поможем ему.

(reported speech; expresses future action).

1. I should have indicated the directions in which the distances were to be measured. 2. We answered that we should explain the methods by which the results had been obtained. 3. The professor said we should determine the equation of that geometric figure. 4. I replied that I should have written the thesis by the end of the year. 5. A circle is a plane curve which should satisfy a unique property. 6. This locus should be investigated by the students. 7. You should have solved more difficult puzzles, because your intelligence is above average. 8. Students should know more about transcendental functions. 9. Any point on the curve should possess the unique property.

Ex. 16. Topics for discussion.

1. Dwell on the fundamental problems of all analytic geometry.

2. Speak on the locus of an equation.

3. Describe the second fundamental problem of analytic geometry.

Ex. 17. Read the text and answer the following questions.

1. What is the parabola? (The ellipse, the hyperbola).

2. What does the equation of the parabola depend on?

3. How do we call the points in which the ellipse cuts the principal axis?

4. Can we consider the notion of correspondence between a geometric locus and an equation as a general concept?

5. Is there any relationship between the parabola, the ellipse and the hyperbola?

Text B

PARTICULAR SPECIES OF LOCI

We shall proceed to the discussion of particular species of loci, namely, a parabola, an ellipse and a hyperbola.

The parabolais the locus of points which are equidistant from a fixed point and a fixed straight line.

The fixed point is the locus, the fixed line is the directrix. The line perpendicular to the directrix and passing through the focus is the axis of the parabola. The axis of the parabola is, obviously, a line of symmetry. The point on the axis halfway between the focus and the directrix on the parabola is the vertex of the parabola. The parabola is fixed when the focus and the directrix are fixed. The equation of the parabola, however, depends on the choice of the coordinate system. If the vertex of the parabola is at the origin and the focus is at the point (О, Р), its equation is X² = 2PY or Y²=2PX.

The ellipseis the locus of a point which moves so that the sum of its distances from two fixed points called the foci is constant. This constant will be denoted by 2a, which is necessarily greater than the distance between the foci (the focal distance). The line through the foci is the principal axis of the ellipse; the points in which the ellipse cuts the principal axis are called the vertices of the ellipse. If the centre of the ellipse is at the origin but the foci are on the y-axis its equation is

Guess the meaning of the followed words. - student2.ru + = 1

where a and b represent the lengths of its semimajor and semiminor axes (большая и малая полуоси).

The hyperbolais the locus of a point which moves so that the difference of its distances from two fixed points is a constant 2a. Its equation is

Guess the meaning of the followed words. - student2.ru - = 1

This equation shows that the hyperbola is symmetric with respect to both coordinate axes and also the origin. It intersects the X-axis but does not cut the Y-axis. Hence, the curve is not contained in a bounded portion of a plane. The curve consists of two branches. The line segment joining the vertices is called the transverse axis of the hyperbola; its length is 2a. The point midway between the vertices is a geometrical centre and is called the centre of the hyperbola.

UNIT V

Pre-Reading Activity

Guess the meaning of the following words:

function (n) ['fANkSn] formula (n) ['fO:mjulq]

graph (n) ['grxf] distance (n) ['dIstqns]

real (a) ['rIql] temperature (n) ['temprItSq]

condition (n) [kqn'dISn] reflect (v) [rI'flekt]

qualify (v) ['kwOlIfaI] assistance (n) [q'sIstqns]

physical (a) ['fIzIkql] special (a) ['speSql]

coordinate (n) [kou'O:dnIt]

Read and learn the following words:

approach (v,n) [q'proutS] приближаться, подходить; подход