ЕН.01«Математика» для заочной формы обучения

Наименование разделов и тем	Содержание учебного материала, практические занятия, самостоятельные работы, проверочные работы обучающихся	Объём часов	Уровень освоения
Раздел 1	Повторение
Формулы сокращенного умножения	Содержание учебного материала: Формулы сокращенного умножения. Свойства степени. Упрощение выражений.	-	1,2
Уравнения. Системы уравнений	Содержание учебного материала: Линейные уравнения. Квадратные уравнения. Биквадратные уравнения. Рациональные уравнения. Иррациональные уравнения. Систем уравнений.
Неравенства. Системы неравенств.	Содержание учебного материала: Неравенства и их виды. Системы неравенств.
	Практическое занятие
	Самостоятельная работа обучающихся
Раздел 2	Функции, их свойства и графики
Функции, их свойства и графики	Содержание учебного материала: Функции и их свойства. Функции, способы её задания. Графики элементарных функций.		1,2
Предел функции	Содержание учебного материала: Предел функции в точке. Предел функции на бесконечности.
	Практическое занятие
	Самостоятельная работа обучающихся
Раздел 3	Показательная и логарифмическая функция
Логарифмы и их свойства	Содержание учебного материала: Степень с действительным показателем. Понятие логарифма. Свойства логарифмов.		1,2
Показатель-ная функция	Содержание учебного материала: Показательная функция. Свойства показательной функции. График показательной функции.
Логарифми-ческая функция	Содержание учебного материала: Логарифмическая функция. Свойства логарифмической функции. График логарифмической функции.
Показатель-ные уравнения и неравенства	Содержание учебного материала: Показательные уравнения Показательные неравенства
Логарифми-ческие уравнения и неравенства	Содержание учебного материала: Логарифмические уравнения Логарифмические неравенства
	Практическое занятие
	Самостоятельная работа обучающихся
Раздел 4	Тригонометрические функции
Тригонометрические функции числового аргумента	Содержание учебного материала: Тригонометрические функции числового аргумента Функция у = sin x и её свойства Функция y = cos x и её свойства Функция y = tg x и её свойства Функция y = ctg x и её свойства Построение графиков тригонометрических функций		1,2
Формулы тригономет-рии	Содержание учебного материала: Формулы приведения Формулы сложения тригонометрических функций Формулы суммы и разности углов Формулы двойного угла. Преобразование тригонометрических выражений
Тригонометрические уравнения и неравенства	Содержание учебного материала: Обратные тригонометрические функции Графики обратных тригонометрических функций Тригонометрические уравнения Тригонометрические неравенства
	Практическое занятие
	Самостоятельная работа обучающихся
Раздел 5.	Производная функции и её приложение
Производная функции. Общее правило дифферен-цирования	Содержание учебного материала: Определение производной функции Общее правило дифференцирования.		1,2
Дифферен-цирование функций	Содержание учебного материала: Производная степенной функции Правила дифференцирования. Производная тригонометрических функций Производная обратных тригонометрических функций Производная показательной и логарифмической функции Производная сложной функции
Геометричес-кий и физический смыслы производных	Содержание учебного материала: Геометрический смысл производной Физический смысл производной
Исследование функции и построение её графика с помощью производной	Содержание учебного материала: Монотонность функции Точки экстремума функции Наибольшее и наименьшее значения функции Полное исследование функции и построение её графика
	Практическое занятие
	Самостоятельная работа обучающихся
Раздел 6.	Интеграл и его приложение.
Неопределён-ный интеграл	Содержание учебного материала: Первообразная функции и её свойства Неопределённый интеграл и его свойства Основные формулы интегрирования Непосредственное интегрирование		1,2
Определён-ный интеграл	Содержание учебного материала: Определённый интеграл и его свойства Геометрический смысл определённого интеграла Вычисление площади криволинейной трапеции Объёмы тел вращения
	Практическое занятие
	Самостоятельная работа обучающихся
Раздел 7.	Векторы в пространстве
Векторы на плоскости	Содержание учебного материала: Векторы на плоскости Основные характеристики Действия над векторами на плоскости		1,2
Векторы в пространстве	Содержание учебного материала: Векторы в пространстве Основные характеристики Действия над векторами в пространстве
Скалярное произведение векторов	Содержание учебного материала: Скалярное произведение векторов Угол между векторами
	Практическое занятие
	Самостоятельная работа обучающихся
Раздел 8.	Прямые и плоскости в пространстве
Прямые и плоскости в пространстве	Содержание учебного материала: Аксиомы стереометрии и следствия из них Взаимное расположение прямой и плоскости в пространстве Взаимное расположения прямых в пространстве Перпендикулярность прямой и плоскости Взаимное расположение плоскостей Двугранные и многогранные углы Перпендикулярность плоскостей		1,2
	Практическое занятие	-
	Самостоятельная работа обучающихся
Раздел 9.	Геометрические тела и их поверхности
Многогран-ники	Содержание учебного материала: Призма Площадь поверхности призмы Параллелепипед и его свойства Объём призмы Пирамида. Площадь поверхности пирамиды Усечённая пирамида Площадь поверхности усечённой пирамиды Объём пирамиды и усечённой пирамиды		1,2
Тела вращения	Содержание учебного материала: Конус Площадь поверхности конуса Усечённый конус и его поверхность Объём конуса и усечённого конуса Цилиндр. Площадь поверхности цилиндра Объём цилиндра Сфера. Уравнение сферы Шар и его части Площадь поверхности шара и его частей Объём шара и его частей
	Практическое занятие
	Самостоятельная работа обучающихся
	Итого

Для характеристики уровня освоения учебного материала используются следующие обозначения:

1. – ознакомительный (узнавание ранее изученных объектов, свойств);

2. – репродуктивный (выполнение деятельности по образцу, инструкции или под руководством)

3. – продуктивный (планирование и самостоятельное выполнение деятельности, решение проблемных задач)

Методические рекомендации для выполнения самостоятельных и контрольных работ

Приступая к изучению предмета необходимо ознакомиться с содержанием программы и составить план занятий, т. е. разделить материал на последовательно изучаемые темы. После этого в каждой теме следует выделить основные вопросы, чтобы затем, в процессе изучения материала, найти на них ответы.

Одним из важнейших средств активизации самостоятельной творческой деятельности студентов является умение решать задачи. Для этого необходимо внимательно изучить условие задачи, проанализировать содержание, выяснить закономерности и правила, лежащие в основе её решения.

Конечно, общих рецептов для решения разнообразных задач не существует, однако рекомендуем придерживаться следующих советов:

1. Внимательно изучите цель, поставленную в задаче; выясните, какие теоретические положения связаны с данной задачей в целом или с некоторыми её элементами.

2. Не следует приступать к решению задачи, не обдумав её условия и не найдя плана решения.

3. Попробуйте расчленить данную задачу на серию вспомогательных, последовательное решение которых может составить решение исходной задачи.

4. Найдя план решения, выполните его, убедитесь в необходимости и правильности каждого шага, произведите проверку решения.

5. Подумайте, нельзя ли было решить задачу иначе; известно, что каждая задача может иметь несколько решений, поэтому следует выделить наиболее рациональное.

6. Если решить задачу не удаётся, отыщите в учебной литературе уже решённую задачу, похожую на данную, изучите внимательно это решение и постарайтесь извлечь из него пользу для решения данной задачи.

Необходимо приучить себя к постоянному самоконтролю в процессе своей работы. При решении задачи следует приучиться проверять каждый свой шаг, оценивать его разумность, рациональность, необходимость и полезность.

При этом могут использоваться различные приемы самоконтроля: проверка результатов решения задачи, проверка по аналогичному заданию, проверка с помощью обратных действий, оценка соответствия результата здравому смыслу.

Решив задачу, проанализируйте решение, отметьте, что нового при этом вы узнали и приобрели. Постарайтесь запомнить и усвоить те приёмы, которые вы использовали. Все это пригодится при решении других задач.

Контрольная работа содержит задания из разных тем. При решении заданий на тему:

- «Уравнения и неравенства» следует применять формулы упрощения многочленов, свойства уравнений и неравенств;

- «Пределы функции в точке и на бесконечности» следует применять определения пределов в точке и на бесконечности, их свойства, понятия бесконечно большой и бесконечно малой величин, уметь раскрывать неопределенности .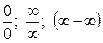

- «Показательная и логарифмическая функции» следует применять свойства степеней, свойства логарифмов, свойства показательной и логарифмической функций:

Свойства степеней:

1). а⁰ = 1

2). а¹ = а

3). (а^m)ⁿ = а^mn

4). а^m·aⁿ = а^m+n

5). 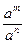= а^m-n

6). (abc)^m = a^m b^mc^m

7). =

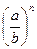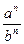
8). =

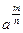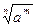
9). 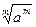= a

10). =

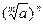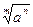
11). =

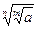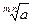
12). =

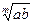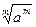
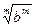
13).

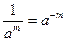
Логарифмом положительного числа b по основанию a, называется показатель степени с, в которую нужно возвести основание а, чтобы получить число b, причём b>0, а>0 и а≠1.

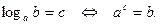Основное логарифмическое тождество:

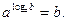Основные свойства логарифмов:

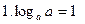(а>0, а≠1);

(а>0, а≠1);

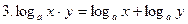(а>0, а≠1, x>0, y>0);

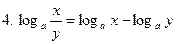(а>0, а≠1, x>0, y>0);

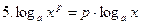(а>0, а≠1, x>0);

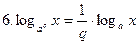(а>0, а≠1, x>0, q≠0);

7. Переход к новому основанию:

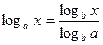(а>0, а≠1, x>0, b>0, b≠1);

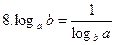(а>0, а≠1, b>0, b≠1).

- «Тригонометрия» следует применять формулы тригонометрии, свойства уравнений и неравенств;

- «Производная функции» следует применять определение производной функции, правила дифференцирования функции, и основные формулы дифференцирования.

Правила дифференцирования:

Пусть U и V – функции переменной x,

С – постоянная величина.

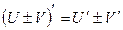
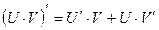
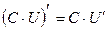
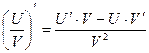
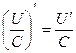
Формулы дифференцирования:
Элементарны функции:	Сложные функции:
1.	-
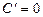2.	-
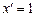3.
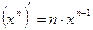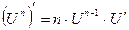4.
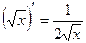5.
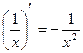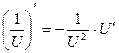6.
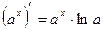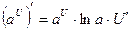7.
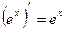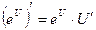8.
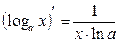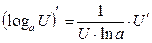9.
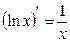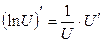10.
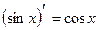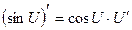11.
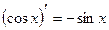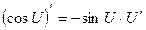12.
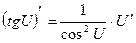13.
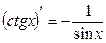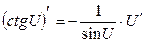14.
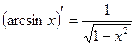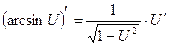15.
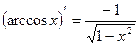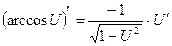16.
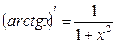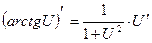17.

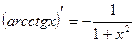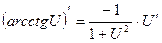- «Неопределённый интеграл» следует применять свойства неопределенного интеграла, основные формулы интегрирования и если после алгебраических преобразований нельзя применить формулы интегрирования, то необходимо воспользоваться методом подстановки, методом интегрирования по частям или методом интегрирования рациональных дробей.