Построение кривой свободной поверхности по трассе канала
Как следует из предыдущего анализа, на границах участков канала (переломах уклона) сопряжение кривых свободной поверхности может быть плавным (если конечная глубина предыдущего участка совпадает с начальной глубиной последующего участка), либо сопровождаться гидравлическим прыжком. При этом положение прыжка необходимо уточнить: он может располагаться непосредственно на границе участков, а может несколько сместиться вверх или вниз по течению. Это зависит от соотношения глубин на границах каналов.
Как известно, гидравлическим прыжком преодолевается перепад глубин потока от глубины меньше критической к глубине больше критической. При этом глубины перед прыжком h' и за прыжком h" (сопряженные глубины) связаны друг с другом уравнением прыжковой функции, которое состоит в том, что прыжковые функции для глубин перед прыжком и за прыжком равны
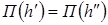 ,
,
где 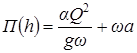 – прыжковая функция.
– прыжковая функция.
Здесь α – коэффициент кинетической энергии (коэффициент Кориолиса), принимаемый равным для турбулентного режима течения α ≈ 1,0;
a – глубина погружения центра тяжести живого сечения.
Для русла с живым сечением трапецеидальной формы глубина погружения центра тяжести равна:
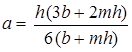 .
.
Для русла с сечением прямоугольной формы, полагая m = 0, получим a = h/2.
Первой сопряженной глубиной (перед прыжком) является конечная глубина участка, расположенного выше по течению. Положение прыжка определяется соотношением второй сопряженной глубины (после прыжка) и начальной глубины на последующем участке. Если глубина за прыжком (вторая сопряженная глубина h") больше глубины в начале участка, расположенного ниже по течению (бытовой глубины hб), то прыжок сдвигается от границы между участками вниз по течению. Если же глубина за прыжком h" меньше бытовой глубины hб последующего участка, то прыжок сдвигается от границы между участками вверх по течению.
Для определения точного места расположения оси гидравлического прыжка используем графоаналитический метод. Для этого необходимо построить график зависимости прыжковой функции от глубины:
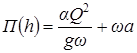 .
.
Для построения графика задаёмся 8 ÷ 9 значениями h больше и меньше hкр. и вычисляем соответствующие им значения прыжковой функции П(h). Вычисления удобнее провести в табличной форме.
Таблица 3.1
Расчет точек прыжковой функции
| № п/п | h, м | ω, м2 | 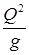 | 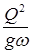 | a, м | aω, м3 | П(h) |
По данным такой таблицы строится график прыжковой функции (рис. 3.1).
Принимая в качестве первой сопряженной глубины (перед прыжком) конечную глубину участка, расположенного выше по течению (как правило, это нормальная глубина h01 или h01 + 1 см), по графику прыжковой функции определяем вторую сопряженную глубину h" и сравниваем её с начальной глубиной на последующем участке.
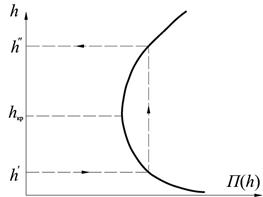
Рис. 3.1. График прыжковой функции П(h)
Здесь, как уже отмечено, возможны два варианта.
1. Первый вариант сопряжения – вторая сопряженная глубина оказывается больше начальной глубины на последующем участке, h" > hб.

Рис. 3.2
Это значит, что ось гидравлического прыжка сместится вниз по течению от места соединения участков (перелома уклона дна). Для того чтобы определить местонахождение оси гидравлического прыжка, построим продолжение кривой свободной поверхности участка, расположенного выше по течению, на нижележащий участок (расчет можно проводить на персональном компьютере либо вручную). В обоих возможных случаях (прыжок на границе первого и второго участков или третьего и четвертого участков, см. рис. 3.2) мы попадаем на участок с малым уклоном (либо меньше критического, либо с нулевым или обратным уклоном). При этом начальная глубина на входе в участок оказывается меньше критической. Поэтому для кривой свободной поверхности возможна только кривая подпора типа c1 или c4 (рис. 3.3).
а 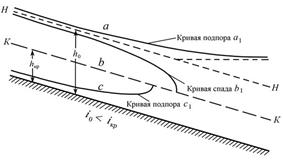 Уклон дна меньше критического Уклон дна меньше критического | б 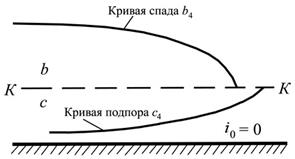 Уклон дна равен нулю Уклон дна равен нулю |
| Рис. 3.3 |
Расчет кривой свободной поверхности на нижележащем участке проводим до достижения этой кривой критической глубины hкр – рис. 3.4.
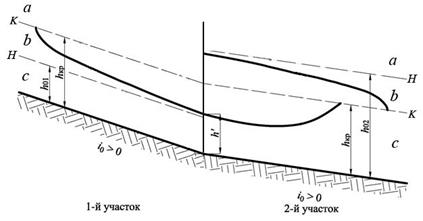
Рис. 3.4
Затем по графику прыжковой функции (рис. 3.1) определяются глубины h", сопряженные выбранным 5 ÷ 6 значениям глубин вновь построенной кривой подпора. По этим значениям строим кривую сопряженных глубин (пунктир на рис. 3.5). Точка пересечения пунктирной кривой сопряженных глубин h" с основной кривой спада на участке определяет местоположение оси прыжка (рис. 3.5).
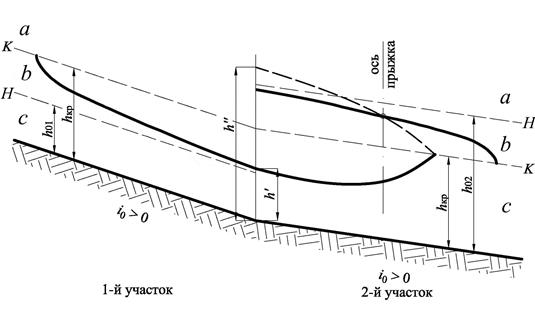
Рис. 3.5
2. Второй вариант сопряжения – вторая сопряженная глубина оказывается меньше начальной глубины на последующем участке, h" < hб.
Тогда ось гидравлического прыжка сместится вверх по течению от места соединения участков (перелома уклона дна). В этом случае для определения положения оси гидравлического прыжка, построим продолжение кривой свободной поверхности участка, расположенного ниже по течению, на предшествующий ему участок. Мы попадаем на нижнюю границу предшествующего участка с большим уклоном с глубиной больше критической (рис. 3.6). Тогда вверх по течению возможна только кривая подпора типа a2 (рис. 3.6). Строим её до пересечения с линией критических глубин. Эта кривая соответствует вторым сопряженным глубинам гидравлического прыжка h" (глубинам после прыжка).
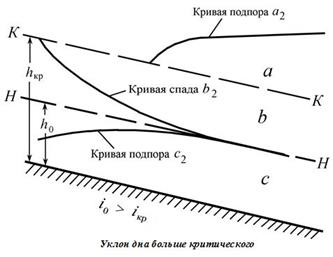
Рис. 3.6
По графику прыжковой функции определяем сопряженные этим глубинам глубины перед прыжком h' и пунктиром строим график этих сопряженных глубин. Точка пересечения пунктирной кривой сопряженных глубин h' с кривой спада свободной поверхности на участке определит положение оси прыжка (рис. 3.7).
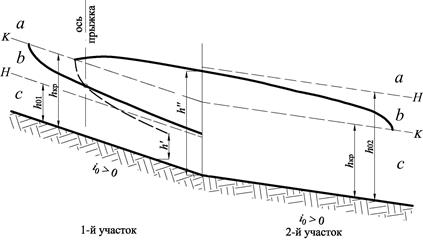
Рис. 3.7
В работе необходимо также определить потери удельной энергии сечения в прыжке ΔЭ. Для этого, используем формулу удельной энергии (1.3)
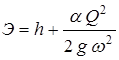 .
.
Потери удельной энергии определятся как разность удельных энергий сечения до прыжка Э(h') и после прыжка Э(h"). Построим график зависимости удельной энергии сечения от глубины, для этого удобно составить таблицу.
Таблица 3.2
| № п/п | h, м | ω, м2 | ω2 | 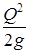 | 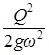 | Э(h), м |
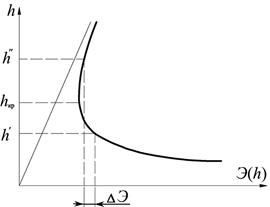
Рис. 3.8
Затем, задаваясь уже определенными значениями сопряженных глубин до прыжка h' и после прыжка h", по графику прыжковой функции определяем потери энергии в прыжке
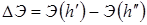 .
.
В заключение работы строится общий график кривой свободной поверхности потока вдоль всей трассы канала. При этом целесообразно использовать разный линейный масштаб по вертикальной и горизонтальной осям, то есть вертикальный масштаб глубин брать крупнее продольного масштаба длин.
ЛИТЕРАТУРА
1. Моргунов К. П. Гидравлика: учебник. СПб.: Издательство «Лань», 2014. – 288 с.
2. Ивановский Ю. К., Рябов Г. Г., Ушакевич А. Н. Гидравлический расчет неравномерного движения воды в каналах: учебно-методическое пособие по выполнению курсовой работы. – СПб.: СПГУВК, 2010 – 34 с..
2. Чугаев P.Р. Гидравлика. — М. Л.: ГЭИ, 1971.
3. Павловский Н.Н. Краткий гидравлический справочник. — М.: Стройиздат, 1940.
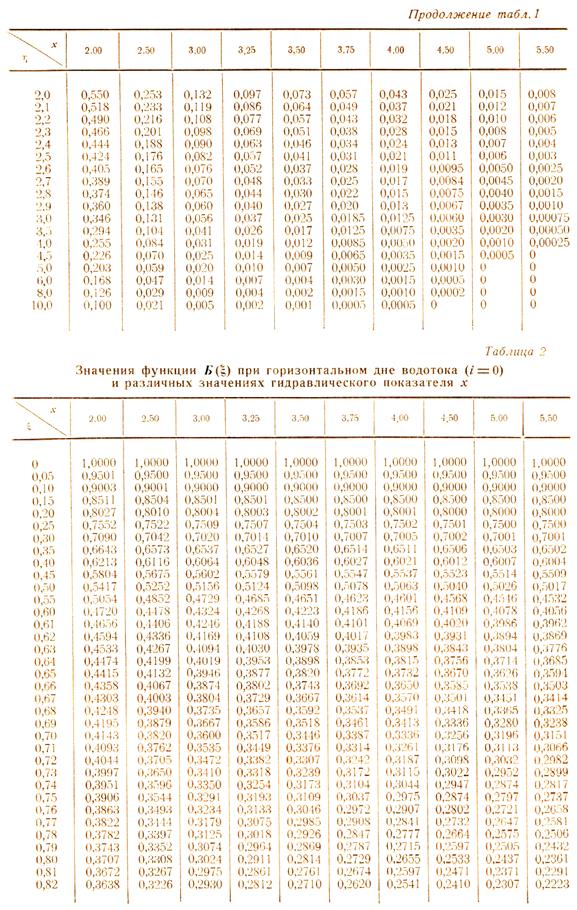
Приложение. Функции Бахметьева







О Г Л А В Л Е Н И Е
| ВВЕДЕНИЕ. Гидравлический расчет неравномерного движения воды в каналах . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |||
| Часть I. Определение нормальных глубин, критической глубины и критического уклона в канале . . . . . . . . . . . . . . . . . . . . . . | |||
| Определения и предварительные замечания . . . . . . . . . . . | |||
| Выполнение расчетов . . . . . . . . . . . . . . . . . . . . . . . . | |||
| 1.1. Определение нормальных глубин для участков канала . | |||
| 1.2. Определение критической глубины потока . . . . . . . | |||
| 1.3. Определение критического уклона . . . . . . . . . . . . | |||
| 1.4. Определение вида свободных поверхностей . . . . . . | |||
| Часть II. Расчет кривых свободной поверхности по участкам канала | |||
| 2.1. Расчет на персональном компьютере . . . . . . . . . . | |||
| 2.2. Расчет ручным способом . . . . . . . . . . . . . . . . . | |||
| Часть III. Расчет гидравлического прыжка. Построение кривой свободной поверхности по трассе канала . . . . . . . . . . . . . . . | |||
| Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |||
| Приложение. Функции Бахметьева . . . . . . . . . . . . . . . . . . . |
