Часть II . Расчет кривых свободной поверхности по участкам канала

Расчет кривых свободной поверхности воды на участках канала проводится по методике, предложенной Б. А. Бахметьевым.

Идея метода Б. А. Бахметьева заключается в следующем. Дифференциальное уравнение, описывающее изменение глубины воды вдоль потока, имеет вид:

.

(2.1)

В это уравнение входит отношение модулей расхода . Это отношение является достаточно сложной функцией глубины, поскольку модуль расхода зависит от геометрических характеристик сечения

,

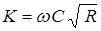а величины ω, C и R порой весьма сложно выражаются через h.

Для облегчения решения задачи Б. А. Бахметьев предложил считать, что связь между K и h устанавливается показательной зависимостью

.

(2.2)

Здесь h₁ и h₂ – две произвольные глубины, взятые для рассматриваемого поперечного сечения русла, а K₁ и K₂ – модули расхода, отвечающие этим глубинам.

Показатель степени xпринимается постоянным для данной формы русла и не зависящим от величины глубин h₁ и h₂. Величина x называется гидравлическим показателем русла.

Не для всех русел существует гидравлический показатель x, который к тому же является постоянной величиной. Однако для многих русел правильной формы такой показатель существует. В частности, для русел прямоугольного и трапецеидального поперечного сечения (а именно такие и рассматриваются в настоящей работе) гидравлический показатель можно считать приблизительно постоянным. Величина гидравлического показателя русла определяется для каждого участка канала по гидравлическим справочникам в зависимости от задаваемого коэффициента заложения откоса канала и отношения средней глубины на рассматриваемом участке к ширине канала по дну . Кроме того, гидравлический показатель русла может быть определен из равенства (2.2) как

,

(2.3)

где K_ср и h_ср – средние значения модуля расхода и глубины на участке канала. Средняя глубина определяется как полусумма начальной и конечной глубин на участке.

Такой подход позволил Б. А. Бахметьеву получить решение уравнения (2.1) для участка канала в виде

.

(2.4)

В этом уравнении используются следующие обозначения:

– относительная глубина;

h₁ и h₂ – действительные глубины в начале и конце участка канала;

– расстояние между сечениями (началом и концом участка канала);

– вспомогательная величина, характеризующая отношение кинетической энергии потока к его потенциальной энергии, значения входящих в формулу параметров рассчитываются для среднего значения глубины на участке ;

α – коэффициент кинетической энергии, принимаемый равным ≈ 1,0;

– функция Бахметьева, значения которой берутся из гидравлических справочников в зависимости от η и x.

Решение (2.4) справедливо для каналов с положительным уклоном (i₀ > 0). Для русел с отрицательным уклоном (i₀ < 0) эта формула примет вид

,

(2.5)

где

и – соответственно «фиктивные» нормальная глубина и уклон;

– относительная «фиктивная» глубина;

– вспомогательная величина;

– функция Бахметьева для «фиктивных» величин.

Для горизонтальных русел с нулевым уклоном (i₀ = 0) решение Бахметьева будет иметь вид

,

(2.6)

где , – относительные глубины;

– вспомогательная величина;

– функция Бахметьева для нулевого уклона.

Расчет кривых свободной поверхности по участкам проводится с использованием программы POTOK, установленной на персональных компьютерах в компьютерном классе кафедры ГТС, К и Г.

На одном из участков канала расчет проводится в ручном режиме.

2.1. Расчет на персональном компьютере.

Перед началом расчета необходимо проверить наличие всех необходимых исходных данных. Основные количественные исходные данные определяются заданием на работу в соответствии с вариантом расчета. Уточнения требует коэффициент шероховатости поверхности дна и откосов канала, входящий в формулу для определения коэффициента Шези. Для определения коэффициента шероховатости в задании приведен характер облицовки: бетон, земля, булыжное мощение. Значения коэффициентов шероховатости приводятся в гидравлических справочниках.

При запуске программы POTOK открывается окно ввода исходных данных (рис. 2.1).

Рис. 2.1

Программа последовательно запрашивает исходные данные и эти данные в соответствии с вариантом расчетного задания необходимо вводить. При этом необходимо учесть следующие особенности программы:

· при вводе десятичных чисел для отделения целой части числа от дробной следует использовать не запятую, а точку;

· если расчет производится от начала участка вниз по течению, то при запросе программы «Начало участка» следует указать «0» (рис. 2.2), при расчете от конца участка вверх по течению в графе «Начало участка» указывается полная длина рассчитываемого участка; в графе «Длина участка» во всех случаях указывается заданная длина рассматриваемого участка;

Рис. 2.2

· при запросе программы «Погрешность» следует указать значение относительной погрешности (в процентах), приемлемой для расчета, рекомендуется значение погрешности 1 – 2 %;

· в графе «Количество участков разбиения» указывается количество участков, на которое разбивается рассматриваемый участок при расчете кривой свободной поверхности, рекомендуется 100 – 120 точек;

· в графе «Количество выводимых точек» указывается количество точек, необходимых для построения графика, 10 – 15 точек.

После введения всей необходимой исходной информации программа запрашивает – верно ли введены исходные данные. При правильном наборе данных необходимо ввести литеру «Y» (рис. 2.3) и программа выводит таблицу значений глубин на участке канала в зависимости от интервалов между глубинами с заданным количеством точек.

Рис. 2.3

На рис 2.4 приведен пример таблицы расчета значений глубин для первого участка канала, при этом уклон участка больше критического, глубина в начале участка задана соотношением h_нач = 0,95h_кр.

Рис. 2.4

Аналогичные расчеты нужно провести и для остальных участков канала. Как видно, для расчета необходимо знать глубину потока на каком-либо конце участка – в начале или в конце. Для определения таких глубин следует воспользоваться результатами анализа, приведенного в первой части работы.

На границе второго и третьего участка, там, где уклон i₀ < i_кр переходит в уклон i₀ ≥ i_кр, устанавливается критическая глубина h = h_кр.

Рис. 2.5

Поскольку глубина устанавливается в конце второго участка, то расчет глубин проводится с конца участка вверх по течению. В графе программы POTOK «Начало участка» устанавливается значение, равное длине участка, в графе «Начальная глубина» – значение критической глубины (рис. 2.5 и 2.6).

Рис. 2.6

Третий участок рассчитывается от начала (от критической глубины) вниз по течению (рис. 2.7 и 2.8).

Рис. 2.7

Рис. 2.8

На четвертом участке известная глубина – заданная глубина в конце участка h_кон = 1,05 h_кр. Поэтому расчет проводится с конца участка вверх по течению (рис. 2.9 и 2.10).

Рис. 2.9

Рис. 2.10

2.2. Расчет ручным способом.

Для расчета ручным способом выбирается участок, глубины которого в начале и в конце участка известны. Таким участком, скорее всего, будет первый участок: глубина в начале него задана h_нач = 0,95h_кр, глубина в конце участка стремится к нормальной. Поскольку отметка свободной поверхности приближается к отметке нормальной глубины асимптотически, если мы примем конечную глубину на участке равную точно h₀, то длина участка будет получаться равной бесконечности. Поэтому конечную глубину потока на первом участке принимаем равной (h₀ + 1 см).

Расчет кривой свободной поверхности проводится по следующей методике.

Разница глубин на концах участка разбивается на несколько (5 – 6) равных интервалов, и затем по методике Б. А. Бахметьева (по формулам (2.4) – (2.6)) рассчитываются расстояния (Δl = l₂ – l₁) между этими интервалами высот. Если расчет проведен правильно, сумма рассчитанных расстояний совпадет с длиной участка.

Для участков с положительным уклоном (а такими являются первые три участка канала) расчет проводится по формуле (2.4).

В начале рассчитываются:

· начальная глубина h_нач = 0,95h_кр;

· конечная глубина h_кон = h₀ + 1 см;

· средняя глубина участка ;

· промежуточные значения гидравлических показателей русла: ширина зеркала B, площадь живого сечения ω, смоченный периметр χ, гидравлический радиус R, коэффициент Шези C; формулы для расчета этих параметров в зависимости от формы живого сечения потока (трапецеидальное или прямоугольное) приведены в первой части работы;

· модули расхода и , где значения с индексом «0» посчитаны для нормальной глубины, а значения с индексом «ср» – для средней глубины;

· гидравлический показатель русла , вычисленное по этой формуле значение гидравлического показателя округляется с точностью до 0,25.

Для расчета удобно составить таблицу промежуточных вычислений.

Таблица 2.1

№	hнач, м	hкон, м	hср, м	B, м	ω, м2	χ, м	R, м	С

Затем производится разбиение глубины потока на всем участке на несколько интервалов (5 – 6). И для каждого из этих интервалов глубины рассчитываются следующие величины:

· j_ср – по формуле, соответствующей уклону участка;

· относительные глубины и .

Далее по гидравлическим справочникам определяются значения функций Бахметьева для соответствующих значений гидравлического показателя x и относительных глубин η₁ и η₂. И по формулам (2.4) – (2.6) (в зависимости от уклона дна участка) определяется длина участка между глубинами h_i и h_{i + 1}.

Таблица 2.1 (продолжение)

№	h1, м	h2, м	jср	η1	η2	Б(η1)	Б(η2)	Δl, м

Проверкой правильности проведенных вычислений является то, что сумма рассчитанных длин будет равна общей длине рассматриваемого участка, ΣΔl = l.

Из-за приблизительности вычисления в ручном режиме полученное суммарное значение рассчитанных длин участков ΣΔl может оказаться не равным заданной длине участка.

Если сумма рассчитанных интервалов оказалась больше заданной длины участка, это значит, что для достижения кривой свободной поверхности к концу участка нормальной глубины требуется длина, большая определенной в задании. А значит, в конце реально заданного участка глубина будет больше нормальной. Тогда необходимо последовательно увеличивать глубину в конце участка (больше принятой изначально h₀ + 1 см), и, проводя заново все расчеты, подобрать такую глубину в конце участка, которая даст равенство сумм рассчитанных длин интервалов заданной длине участка.

Если сумма рассчитанных интервалов окажется меньше заданной длины участка, это значит, что равномерный характер течения устанавливается ещё до достижения потоком конца участка, и далее до конца участка течение продолжается с глубиной, равной нормальной.

По результатам расчета ручным способом строится профиль глубин на участке в зависимости от длины интервалов. При этом масштабы по длине и глубине участка следует брать разными, чтобы удобнее строить профиль.