Алгебраический критерий устойчивости гурвица
Определение устойчивости САУ с использованием алгебраического критерия Гурвица, выполняется следующим образом.
Из коэффициентов характеристического уравнения системы строится определитель Гурвица D по алгоритму:
1) по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от a1 до an;
2) от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз;
3) на место коэффициентов с индексами меньше нуля или больше n ставятся нули;
4) количество строк и столбцов соответствует порядку характеристического уравнения
Число определителей Гурвица равно порядку характеристического уравнения n.
Автоматическая система, описываемая характеристическим уравнением:
,
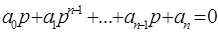устойчива, если при a0>0 положительны все определители ∆1, ∆2, . . .∆п вида
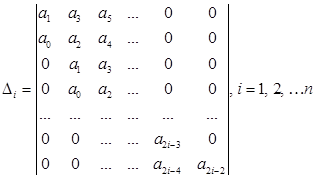
Если хотя бы один из определителей, называемых определителями Гурвица, отрицателен, то система неустойчива.
Если n-й определитель ∆п=0, а все остальные определители положительны, то система находится на границе устойчивости.
Рассмотрим частные случаи критерия Гурвица для n=1;2;3;4. Раскрывая определители, фигурирующие в общей формулировке критерия, можно получить следующие условия.
1. Для уравнения первого порядка (n=1)
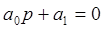
условие устойчивости: а0>0 и ∆1=а1>0, т.е. для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля.
2. Для уравнения второго порядка (n=2)
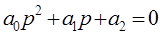
условие устойчивости:
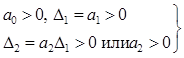
Т.о., и для системы второго порядка необходимое условие устойчивости (положительность коэффициентов) является одновременно и достаточным.
3. Для уравнения третьего порядка (n=3)
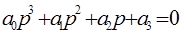
условие устойчивости:
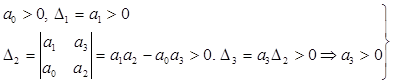
При n=3 для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля и произведение средних коэффициентов уравнения (а1, а2) было больше произведения крайних (а0, а3).
4. Для уравнения четвертого порядка (n=4)
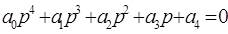
кроме положительности всех коэффициентов требуется выполнение условия
.
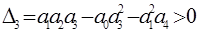При n=4 система будет устойчива при всех коэффициентах больших нуля и при
.
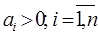Т.о., для устойчивости систем не выше четвертого порядка необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и определитель ∆п-1 были положительными.
Критерий Гурвица применяют при n ≤ 5. При больших порядках возрастает число определителей, и процесс становится трудоемким. Недостаток критерия Гурвица - малая наглядность. Достоинство - удобен для реализации на ЭВМ.
При n>5 критерий Гурвица становится громоздким и применяют критерий Рауса.
Пример. Определение степени устойчивости системы по заданной ПФ с использованием критерия Гурвица.
Пусть передаточная функция разомкнутой системы задана в виде:
W(s) = k/s(T1s +1)(T2s +1)
Исследовать устойчивость системы.
Передаточная функция замкнутой системы:
Wзс(p) = W(p)/[1 + W(p)], ()
где W(p) - передаточная функция разомкнутой системы. (см.Давыдов 4.1.9)
Р е ш е н и е . Характеристическое уравнение замкнутой системы:
D(p)=0, где D(p) =1+W(s)
при s = p получим:
p(T1p+1)(T2p+1)+ k = 0
Раскрыв скобки, получим характеристическое уравнение 3-го порядка:
T1T2p3 + (T1 + T2)p2 + p + k = 0.
Тогда для данного характеристического уравнения имеем следующие коэффициенты:
a0 = T1T2; a1 = (T1 + T2); a2 = 1; a3 = k.
Коэффициенты положительны.
Составим матрицу Гурвица, найдем определители этой матрицы.
Для устойчивости системы все они должны быть положительными:
Δ1 = a1, откуда (T1 + T2) > 0; т.к. постоянные времени не могут быть отрицательными по физическому смыслу.
Δ2 = a1×a2 − a0 ×a3, откуда (T1 + T2) − k·T1·T2 > 0;
Δ3 = a1×a2×a3 − a0×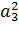 
= a3( a1×a2 − a0×a3 ),
откуда a3 >0 , то есть k > 0.
Условие устойчивости по критерию Гурвица получает вид:
Из определителя Δ2 имеем: (T1 + T2) > k·T1·T2 или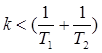 
С учетом вышеуказанного можно определить:
1) an = 0, k = 0;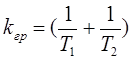 
2) Δn-1 = 0,
3) a0 = 0, T1·T2 = 0.
Используя данный прием, можно определить степень устойчивости системы, зная её ПФ , а также вычислить границы устойчивости замкнутой системы.
ЛЕКЦИЯ № 10