Корневые методы исследование устойчивости сау

Понятие устойчивости системы управления связано со способностью возвращаться в состояние равновесия после исчезновения внешних воздействий, которые вывели ее из этого состояния. Данное определение является физическим определением понятия устойчивости.

Это означает, что если система выведена из состояния равновесия каким-либо возмущением, то она возвращается в исходное состояние после устранения этого возмущения, т.е. устойчивость системы определяется ее свободным движением. Примером, может служить маятник, который качнули.

Одним из направлений исследования устойчивости систем является использование корневых условий, т.е. определение устойчивости линейных динамических систем по их уравнениям.

При этом устойчивость линейной динамической системы может быть определена по характеру её cвободного движения,т.е. движения, которое появляется в системе после подачи и снятия возмущающего воздействия, при равенстве нулю задающего и возмущающих входных воздействий.

А.М.Ляпуновым доказано, что если система движущаяся свободно будет устойчива, то будет устойчива и система с вынужденным движением, на которую возмущение действует постоянно. Однако анализ на устойчивость первой значительно проще.

Таким образом, вопрос устойчивости сводится к выяснению устойчивости свободного движения системы и требует анализа характера решения уравнения свободного движения, составленного относительно отклонения выходной величины y(t)от установившегося состояния.

Свободное движение линейной или линеаризованной системы описывается однородным дифференциальным уравнением:

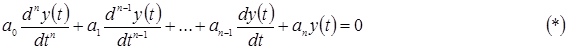
где 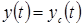- свободная составляющая выходной величины системы.

Система является устойчивой, если свободная составляющая[1] y_c(t) переходного процесса с течением времени стремится к нулю, т.е. если

.

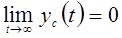Такая устойчивость называется асимптотической.

Если свободная составляющая неограниченно возрастает, т.е. если

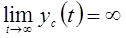то система неустойчива.

Наконец, если свободная составляющая не стремится ни к нулю, ни к бесконечности, то система находится на границе устойчивости.

Найдем общее условие, при котором система, описываемая уравнением (*), устойчива.

Решение уравнения (*) равно сумме:

где C_k – постоянные интегрирования, определяемые параметрами системы и начальными условиями;

p_k – корни характеристического уравнения:

.

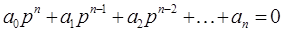Данное характеристическое уравнение - это приравненная нулю сумма полинома числителя и полинома знаменателя передаточной функции разомкнутой системы или приравненный нулю полином знаменателя передаточной функции замкнутой системы, корни которого являются полюсами передаточной функции (см.раздел 2.5).

Иллюстрацией к сказанному выше является следующее:

передаточная функция разомкнутой системы равна

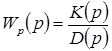, (5-6)

а для замкнутой с единичной обратной связью

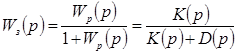(5-7)

Поэтому характеристическое уравнение для замкнутой системы имеет вид:

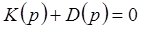(5-8)

для разомкнутой системы:

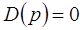(5-9)

Корни уравнения (**) могут быть вещественными (p_k=a_k), мнимыми (p_k=jb_k) и комплексными (p_k=a_k± jb_k).

При этом вещественные (действительные) корни рассматриваются как частный случай комплексных корней, у которых мнимая часть равна нулю.

Переходная составляющая по выражению (**) при t®¥ стремится к нулю лишь в том случае, если каждое слагаемое вида .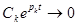

Характер этой функции времени зависит от вида корня p_k. Рассмотрим все возможные случаи расположения корней p_k на комплексной плоскости (см. рис.4.1) и соответствующие им функции y_k(t), которые показаны внутри кругов.

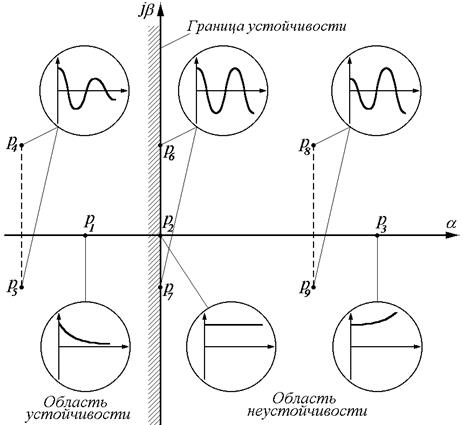
Рис.4.1

Каждому вещественному корню p_k=a_k в решении (**) соответствует слагаемое вида

Если a_k<0 (корень р₁), то функция (***) при t®¥ стремится к нулю. Процесс является затухающим апериодическим.

Если a_k>0 (корень р₃), то функция (***) неограниченно возрастает. Процесс является расходящимся апериодическим.

Если a_k=0 (корень р₂), то функция (***) остается постоянной. Процесс является устойчивостью нейтрального типа.

Каждой паре сопряженных комплексных корней p_k=a_k± jb_k в решении (**) соответствуют два слагаемых, объединенных в одно

Эта функция представляет собой синусоиду с частотой b_k и амплитудой, изменяющейся во времени по экспоненте.

Если вещественная часть двух комплексных корней a_k<0 (корни р₄ и р₅), то колебательная составляющая (****) будет затухать. Процесс является затухающим колебательным.

Если a_k>0 (корни р₈ и р₉), то амплитуда колебаний будет неограниченно возрастать. Процесс является расходящимся колебательным.

Наконец, если a_k=0 (корни р₆ и р₇), т.е. если оба сопряженных корня – мнимые (p_k=+ jb_k, p_k+1=- jb_k), или если хотя бы один комплексно-сопряженный корень имеет нулевую вещественную часть, то x_k(t) представляет собой незатухающую синусоиду с частотой b_k. Процесс является незатухающим колебательным.

Необходимо иметь ввиду, что выражение (**) представляет собой сумму слагаемых вида (***) и анализ устойчивости системы определяется по совокупности расположения корней (полюсов) на комплексной плоскости.

Обобщая вышеуказаннные рассуждения, можно сделать следующие выводы:

· Для устойчивости линейной автоматической системы управления необходимо и достаточно, чтобы вещественные части всех корней характеристического уравнения системы были отрицательны.

· Если хотя бы один корень имеет положительную действительную часть, то система будет неустойчивой.

Используя геометрическое представление корней на комплексной плоскости (см. рис.4.1.) в виде векторов или точек, можно дать вторую формулировку общего условия устойчивости(эквивалентную основной):

· Для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения находились в левой полуплоскости.

· Если хотя бы один корень находится в правой полуплоскости, то система будет неустойчивой.

· Мнимая ось jb является границей устойчивости в плоскости корней.

· Если характеристическое уравнение имеет одну пару чисто мнимых корней (p_k=+jb_k, p_k+1=-jb_k), а все остальные корни находятся в левой полуплоскости, то в системе устанавливаются незатухающие гармонические колебания с круговой частотой 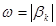. В этом случае говорят, что система находится на колебательной границе устойчивости.

· Точка b =0 на мнимой оси соответствует так называемому нулевому корню (корень р₂) . Если уравнение имеет один нулевой корень, а остальные корни этого уравнения отрицательные, то система находится на апериодической границе устойчивости (система нейтрально устойчива). Нулевой ко­рень появляется, когда свободный член характеристиче­ского уравнения равен нулю.

· Если таких корня два, то система неустойчива.

Определение устойчивости САУ по полюсам ее передаточной функции называют прямым методом оценки устойчивости.

Пример.

Движение системы описывается дифференциальным уравнением

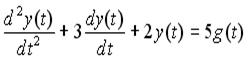
где: y(t) - выходная переменная, g(t) - задающее воздействие, t - время.

Требуется определить характер устойчивости данной автоматической системы …

Решение.

Характеристическое уравнение для данной системы имеет вид:

D_(s) = s²+3s+2=0.

Найдем корни этого уравнения

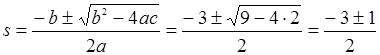
Откуда: s₁= -1, s₂= -2.

Поскольку характеристическое уравнение системы имеет только отрицательные корни можно сделать заключение, что она устойчива.

Таким образом, исследование устойчивости системы сводится к определению знаков вещественных частей корней характеристического уравнения системы. Но решение уравнений четвертой и более высоких степеней может встречать затруднения. Поэтому применяются косвенные методы анализа устойчивости без определения корней характеристического уравнения, по определенным критериям устойчивости.

Имеются также методы, позволяющие судить об устойчивости системы по так называемым условиям устойчивости, не решая характеристического уравнения и не находя его корней [55,56].

Первым таким условием (условие устойчивости А.Стодолы) является следующее: система будет устойчивой, если все коэффициенты ее характеристического уравнения положительны.

Примечание. Заметим, что это условие можно сформулировать и по другому: все коэффициенты характеристического уравнения должны быть отрицательными, т.к. умножая характеристическое уравнение на минус единицу, можно сделать все коэффициенты положительными.

Таким образом, для обеспечения условия устойчивости можем говорить об одинаковости знаков характеристического уравнения.

Если все коэффициенты характеристического полинома а > 0, то любое действительное положительное значение s, подставленное в уравнение, не может обратить его в нуль и, следовательно, не является корнем характеристического уравнения. Поэтому при а > 0 невозможно появление нарастающих экспонент, характеризующих апериодическую неустойчивость, т.е. апериодическая неустойчивость невозможна. Однако может возникнуть колебательная неустойчивость, т.е. появление в решении составляющих в виде колебаний с нарастающей амплитудой. Это возникает, когда существуют комплексно-сопряженные корни с положительной действительной частью. Поэтому условие положительности коэффициентов при порядке системы больше двух является необходимым условием, но не достаточным, а для уравнений первого и второго порядка это условие является и достаточным.

К сожалению, условие Стодолы является и необходимым и достаточным, только если порядок характеристического уравнения САР не превышает двух, т.е. при n =1 и n =2. Если же 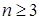, то условие Стодолы дает только необходимые условие, но не достаточные. К примеру, характеристическое уравнение второго порядка

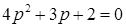
имеет все положительные коэффициенты, поэтому САР с таким уравнением устойчива.

Для исследования устойчивости САУ используют также алгебраические и критерии Вышнеградского, Гурвица, Льенара-Шипаро, Рауса, и частотные критерии Найквиста, Михайлова и другие.

В литературе по САУ встречаются следующие рекомендации по применению критериев устойчивости:

1. Алгебраический критерий Гурвица целесообразно применять при порядке системы .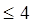

2. Алгебраический критерий Рауса применяется при порядке системы от 4 до 6.

3. Критерий устойчивости Михайлова применяется при исследовании сложных многоконтурных систем, когда необходимо выяснить влияние измерения структуры системы и средств ее стабилизации на устойчивость.

4. Критерий устойчивости Найквиста целесообразно применять тогда, когда система имеет одноконтурный вид, и если отдельные элементы системы заданы экспериментально.

5. Логарифмический критерий устойчивости применяется тогда же, когда и критерий Найквиста, особенно при исследовании системы на большом интервале частот.