Структурное представление сау

Изображение САУ в виде совокупности однонаправленных типовых звеньев с указанием связей между ними и внешней средой называется структурной схемой САУ (точнее, алгоритмической структурной схемой или просто структурой САУ), которая является графической интерпретацией описания математической модели САУ передаточными функциями (ПФ). Данный способ составляет сущность структурного метода представления, расчетов и исследования САУ различной физической природы, который дает наглядное представление о взаимосвязи элементов, звеньев и частей САУ и позволяет оценивать основные свойства переходных и установившихся процессов в САУ [50].

На структурных схемах САУ (рис. 1.4.1) каждое звено обозначается прямоугольником, в котором записывается ПФ звена или её обозначение. Входные воздействия обозначаются стрелками, направленными в звено, выходные величины — стрелками, направленными из звена. Сумматоры обозначаются кружком, в который направлены стрелки суммируемых величин (вычитаемые величины обозначаются с минусом около стрелки), а результирующая величина обозначается стрелкой, выходящей из кружка.

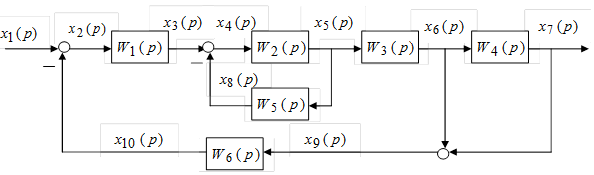
Рис. 1.4.1 — Структурная схема САУ

В однонаправленных звеньях отсутствует влияние выходной величины на входное воздействие. Устройства САУ, в которых имеется обратная связь, представляются в структурной схеме контуром с обратной связью. Например, на рис. 1.4.1 контур с обратной связью состоит из звена W₂(p) прямой связи, звена W₅(p) отрицательной обратной связи и сумматора, в котором сигнал x₈(p)отрицательной обратной связиуменьшает входное воздействие x₃(p) на звено W₂(p)до значения x₄(p). Структурная схема составляется по функциональной схеме САУ с учётом математического описания процессов управления, происходящих в звеньях САУ.

Используются следующие основные правила эквивалентных преобразований структурных схем:

1. Преобразование последовательно соединенных звеньев.

Последовательным называют такое соединение звеньев, при котором выходная величина предыдущего звена является входной для последующего (рис. 3.6.1).

Рис. 3.6.1

При известных передаточных функциях звеньев, можно записать:

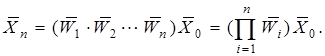(1.4.1)

Таким образом, систему из неограниченного количества звеньев, включенных последовательно, можно заменить одним эквивалентным звеном с передаточной функцией W(i) равной произведению передаточных функций звеньев. Упрощенно для двух звеньев это можно записать так:

W(p) = W₁(p) W₂(p).

2. Преобразование параллельно соединенных звеньев:

При параллельном соединении звеньев на все входы подается одна и та же величина, а выходная величина равна сумме выходных величин отдельных звеньев (рис. 3.6.2).

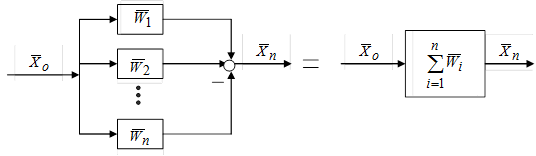
Рис. 3.6.2

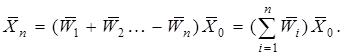(1.4.2)

Из последнего выражения следует, что параллельное соединение звеньев эквивалентно одному звену с передаточной функцией, равной сумме передаточных функций, входящих в соединение звеньев. Упрощенно для двух звеньев это можно представить так:

W(p) = W₁(p)+W₂(p)

3. Правило преобразования контура с обратной связью.

При встречно-параллельном соединении звеньев на вход звена кроме входной подается еще и выходная величина через специальное звено обратной связи. На рис. 3.6.3 звено W₁(p) составляет прямую цепь, которая охвачена ОС, звеном W₂(p). При этом если сигнал x₂ вычитается из входного сигнала x₀, то ОС называется отрицательной, а если суммируется, то ОС – положительная.

Для представленной схемы обратной связи имеем:

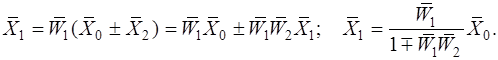(1.4.3)

Отсюда для схемы из двух звеньев с обратной связью передаточную функцию можно представить так:

W(p) = W₁(p) /(1+ W₁(p)W₂(p)).

4. Правила переноса узла разветвления сигнала:

а) по направлению распространения сигналов:

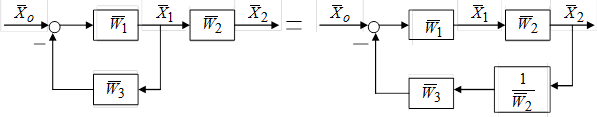
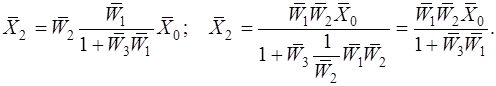(1.4.4)

б) против направления распространения сигналов:

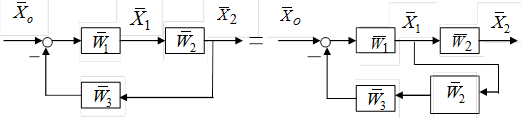
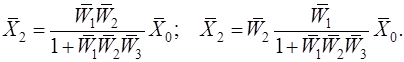(1.4.5)

5. Правила переноса сумматора сигналов:

а) по направлению распространения сигналов:

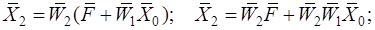(1.4.6)

б) против направления распространения сигналов:

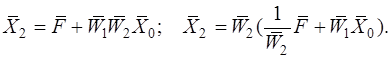(1.4.7)

6. Правила перестановка сумматоров в структурных схемах с перекрещивающимися обратными связями для выделения явно выраженных замкнутых контуров управления.

Перестановка сумматоров выполняется в два этапа. Например, в структурной схеме:

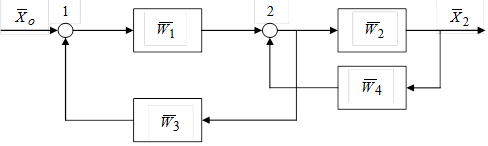
а) на первом этапе преобразования сумматоры совмещают в ближайшем к входу канале по правилу 5,б:

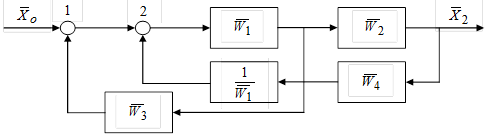
б) на втором этапе преобразования сумматоры переставляют местами в совмещенном канале так, чтобы образовались явно выраженные замкнутые контуры с обратной связью, которые преобразуются по правилу 3:

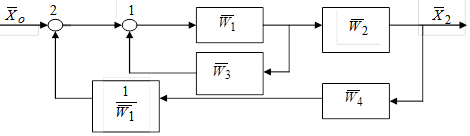
Алгоритмическая структура САУ получается на основе правил эквивалентных преобразований структурных схем. При учете нескольких возмущающих воздействий, для каждого из них выделяется отдельный канал влияния на управляемую величину. В решении задач анализа и синтеза САУ обычно используются следующие три типовые передаточные функции замкнутой САУ с выделенным каналом влияния возмущения f(t) на выходную величину y(t).

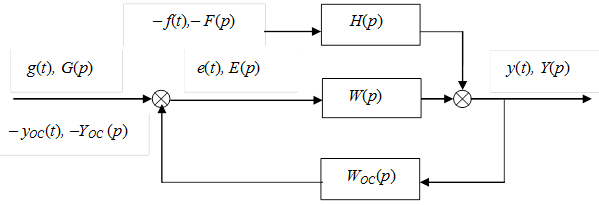
Рис. 1.5.1 — Структура САУ с выделенным каналом возмущения

1. Передаточная функция замкнутой САУ по задающему воздействию g(t) (при отсутствии возмущающих воздействий f(t) = 0):

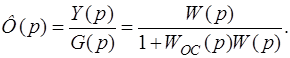(1.5.1)

2. Передаточная функция замкнутой САУ по ошибке e(t) (при отсутствии возмущающего воздействия f(t) = 0):

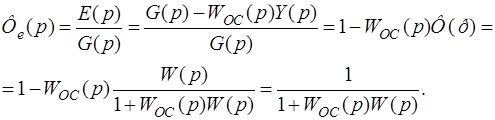(1.5.2)

3. Передаточная функция замкнутой САУ по возмущающему воздействию f(t) (при отсутствии задающего воздействия g(t) = 0):

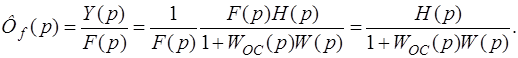(1.5.3)

Все три передаточные функции замкнутой САУ имеют одинаковые характеристические уравнения, что указывает на идентичность динамических свойств САУ по любому каналу управления.

ПОСТРОЕНИЕ ЛАЧХ и ЛФЧХ САУ

Представление САУ в виде совокупности однонаправленных типовых звеньев и получение общей передаточной функции (ПФ) системы, дает возможность построения ЛАЧХ и ЛФЧХ с учетом названных характеристик составляющих её типовых звеньев.

При исследовании и проектировании САУ часто используют АФЧХ, ЛАЧХ и ЛФЧХ разомкнутых систем. Это объясняется тем, что разомкнутые САУ более просто исследовать экспериментально, чем замкнутые. В то же время по ним можно получить исчерпывающую информацию о поведении данной САУ в замкнутом состоянии.

Разомкнутая одноконтурная САУ состоит из цепочки последовательно соединенных динамических звеньев. В соответствии с тем, что передаточная функция разомкнутой одноконтурной системы равна произведению передаточных функций отдельных звеньев, ЛАЧХ и ЛФЧХ разомкнутой САУ строят путем графического сложения ЛАЧХ и ЛФЧХ звеньев.

Для построения ЛАЧХ и ЛФЧХ рекомендуется следующий порядок:

1. Раскладывают сложную передаточную функцию на множители, являющиеся передаточными функциями типовых динамических звеньев, располагая их в порядке убывания постоянной времени Т;

2. Определяются частоты сопряжения и расставляются по оси абсцисс, т.е.

частотная область разбивается на диапазоны, границы которых определяются сопрягающими частотами, соответствующими постоянным времени передаточной функции:

=

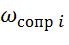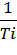
Число сопрягающих частот равняется числу постоянных времени в передаточной функции, а число частотных диапазонов на единицу больше. Получаемые диапазоны соответственно называют низкочастотный, среднечастотный, высокочастотный.

3. Первая низкочастотная асимптота ЛАХ, которая проводится в крайнем левом низкочастотном диапазоне, находится следующим образом.

Для частотной передаточной функции при отсутствии оператора Лапласа S (не входящего в многочлен) в числителе и знаменателе передаточной функции первая асимптота есть прямая линия, параллельная оси абсцисс и проходящая от нее на расстоянии 20·К дБ/дек, где К – передаточный коэффициент.

Для частотной передаточной функции при S в числителе первая асимптота это прямая линия с наклоном + (20×r)дБ/дек и проходит через точку с координатами: 𝟂=1с^-1, L(1)=20lg k дБ, где r - показатель степени оператора Лапласа S, записанного в числителе передаточной функции (не входящего в многочлен).

Для частотной передаточной функции при S в знаменателе первая асимптота это прямая линия с наклоном − (20×r)дБ/дек и проходит через точку с координатами: 𝟂=1с^-1, L(1)=20lg k дБ, где r - показатель степени оператора Лапласа s, записанного в знаменателе передаточной функции (не входящего в многочлен).

4. На сопрягающих частотах ЛАХ претерпевает изломы.

4.1. Если сопрягающая частота соответствует постоянной времени Тi, находящейся в знаменателе передаточной функции, то ЛАХ делает излом вниз на −(20×v) дБ/дек, где v - порядок типового динамического звена, в которое входит эта постоянная времени Тi ( показатель степени S для данного Тi).

4.2. Если сопрягающая частота соответствует постоянной времени Тi, находящейся в числителе передаточной функции, то ЛАХ делает излом вверх на +(20×v) дБ/дек, где v - порядок типового динамического звена, в которое входит эта постоянная времени Тi.

5. Вторая асимптота проводится до следующей сопрягающей частоты и так далее.

6. При построении ЛАЧХ САУ можно использовать конфигурации ЛАЧХ звеньев, входящих в САУ из соответствующих таблиц (например, 1.2.1).

Пример. Построить ЛАХ звена, имеющего следующую передаточную функцию:

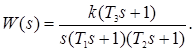
где k = 100 с^-1; Т₁= 5 с; Т₂= 0.01 с; Т₃= 0.5 с.

Решение .

1. Представим передаточную функцию, как произведение ПФ типовых звеньев:

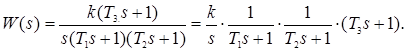
2. Находим сопрягающие частоты:

_сопр1 = 1/Т₁= 0,2 с^-1;

_сопр2 = 1/Т₂=100 с^-1;

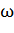_сопр3 = 1/Т₃= 2 с^-1.

3. Строим ЛАХ:

3.1. Частотную область разбиваем на четыре диапазона с учетом того, что

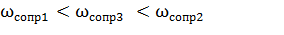
3.2. Низкочастотный участок ЛАХ имеет наклон

−(20×r)= −(20×1)= −20дБ/дек и проходит через точку с координатами:

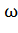= 1с-¹,

L(1) = 20lg k = 40дБ (точка А[1,40]).

3.3. На частоте 1/Т₁ ЛАХ делает излом вниз на

−(20×v)= −(20×1)= −20дБ/дек.

3.4. На частоте 1/Т₃ ЛАХ делает излом вверх на

−(20×v)= (20×1)= 20дБ/дек.

3.5. На частоте 1/Т₂ ЛАХ делает излом вниз на

−(20×v)= −(20×1)= −20дБ/дек.

Вид полученной ЛАХ приведен на рис. 3.13.

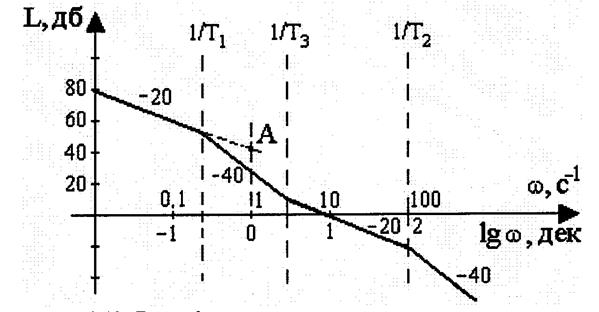
Рис. 3.13.

Рассмотрим также часто встречающуюся задачу определения величины наклона ЛАЧХ при заданной частоте [52].

Указать величину наклона ЛАЧХ с передаточной функцией

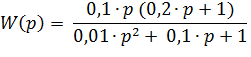
при частоте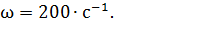

Решение:

САУ содержит следующие типовые звенья (табл.1.2.1): дифференцирующее (8) с коэффициентом передачи k = 0.1, форсирующее (10) с постоянной времени 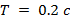и колебательное (4) с постоянной времени 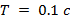и с коэффициентом демпфирования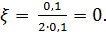

Определим частоты сопряжения для построения асимптотической ЛАЧХ САУ.

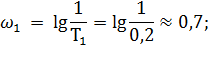
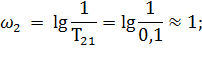
При 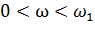ЛАЧХ (рис.12) имеет наклон +20 дБ/дек, обусловленный дифференцирующим звеном. При 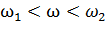наклон ЛАЧХ равен сумме наклонов ЛАЧХ дифференцирующего (+20 дБ/дек) и форсирующего (+20 дБ/дек) звеньев, то есть +40 дБ/дек.

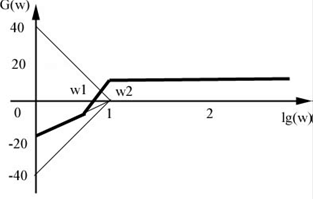
Рис.12. ЛАЧХ системы

При 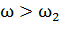«включается» колебательное звено, коэффициент наклона ЛАЧХ для которого равен -40 дБ/дек. Итак, суммарный наклон ЛАЧХ при частоте 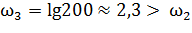будет равен + 20 + 20 − 40 = 0 . Ответ: 0.

Часто возникает необходимость в решении обратной задачи, т.е. по заданной ЛАЧХ системы найти вид её передаточной функции.

Например[52]. Задана последовательность наклонов ЛАЧХ:

0 на уровне 40 дБ при 1 < ω < ω₁= 2 ,

-20 дБ/дек при ω₁ < ω < ω₂= 5,

0 при ω₂ < ω < ω₃= 10,

-20 дБ/дек при ω > ω_3.

Требуется восстановить передаточную функцию САУ по этим данным, представив ответ в виде дроби с полиномами в числителе и знаменателе, записанным в порядке убывания степени оператора Лапласа р,

Решение:

В соответствии заданными наклонами ЛАЧХ и частотами сопряжения, САУ содержит следующие последовательно соединенные звенья: пропорциональное (усилительное, безинерционное) с коэффициентом передачи

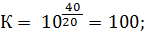
апериодическое (инерционное) с постоянной времени

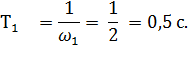
форсирующее с постоянной времени

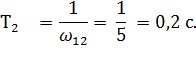
апериодическое (инерционное) с постоянной времени

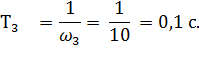
Передаточная функция САУ будет иметь вид:

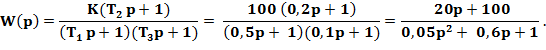
КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Основные правила эквивалентных преобразований структурных схем.

2. Виды передаточные функции замкнутой САУ и их формулы.

3. Порядок построения ЛАЧХ и ЛФЧХ разомкнутых систем.

ЛЕКЦИЯ № 9