Предел и непрерывность функции двух переменных
Основные понятия
Функции двух переменных
Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции нескольких переменных.
Например, площадь 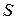 прямоугольника есть функция двух независимо друг от друга изменяющихся переменных – длин сторон прямоугольника
прямоугольника есть функция двух независимо друг от друга изменяющихся переменных – длин сторон прямоугольника  и
и  , которая выражается формулой:
, которая выражается формулой:
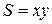 .
.
Работа 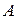 постоянного электрического тока является функцией от разности потенциалов
постоянного электрического тока является функцией от разности потенциалов 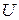 на концах участка, силы тока
на концах участка, силы тока 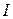 и времени
и времени 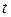 , которая выражается формулой
, которая выражается формулой
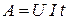 .
.
Например, функция
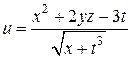
есть функция от четырех переменных 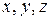 и
и 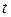 .
.
Остановимся на случае двух переменных, которые будем обозначать  и
и  .
.
Каждой паре значений  и
и  соответствует точка на плоскости
соответствует точка на плоскости 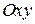 , координатами которой они служат. Рассмотрим некоторое множество точек на плоскости
, координатами которой они служат. Рассмотрим некоторое множество точек на плоскости 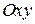 и обозначим его через
и обозначим его через 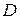 , т.е.
, т.е. 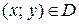 . Надо отметить, что переменные
. Надо отметить, что переменные  и
и  не зависимы друг от друга.
не зависимы друг от друга.
Определение 1.1. Если каждой паре 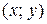 из некоторой области их изменения
из некоторой области их изменения 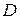 , поставлено в соответствие определенное значение величины
, поставлено в соответствие определенное значение величины 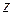 , то говорят, что
, то говорят, что 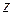 есть функция двух независимых переменных
есть функция двух независимых переменных  и
и  . Записывается
. Записывается
 .
.
При этом  и
и  называются независимыми переменными (аргументами), а
называются независимыми переменными (аргументами), а 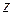 - зависимой переменной (функцией).
- зависимой переменной (функцией).
Определение 1.2. Множество пар 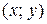 значений
значений  и
и  , при которых определена функция
, при которых определена функция  , называется областью определения функции, обозначается
, называется областью определения функции, обозначается 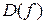 .
.
Если каждую пару значений  и
и  можно изобразить точкой на плоскости
можно изобразить точкой на плоскости 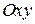 , то область определения функции изобразиться в виде некоторой совокупности точек этой плоскости. В частности, область определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями.
, то область определения функции изобразиться в виде некоторой совокупности точек этой плоскости. В частности, область определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями.
Определение 1.3. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой.
Пример 1.1. Найти область определения 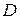 функции
функции
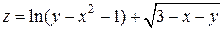 .
.
Решение. Областью определения данной функции является множество точек плоскости 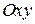 , которые удовлетворяют решению системе неравенств
, которые удовлетворяют решению системе неравенств
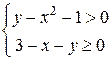 .
.

,
Определение функции двух переменных легко обобщить на случай трех или более переменных.
Определение 1.4. Если каждой рассматриваемой совокупности значений переменных 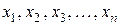 соответствует определенной значение переменной
соответствует определенной значение переменной 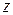 , то
, то 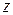 называют функцией независимых переменных
называют функцией независимых переменных 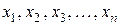 и записывают
и записывают
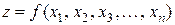 .
.
Так же как и для функции двух переменных, можно говорить об области определения функции трех, четырех и более переменных. Так, например, для функции трех переменных областью определения является некоторая совокупность троек чисел 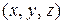 , которые представляют совокупность точек пространства. Область определения функции четырех и более числа переменных уже не допускает простого геометрического истолкования.
, которые представляют совокупность точек пространства. Область определения функции четырех и более числа переменных уже не допускает простого геометрического истолкования.
Функция двух переменных, как и функция одной переменной, может быть задана разными способами: таблицей, аналитически, графически.
Рассмотрим функцию  , определенную в области
, определенную в области 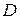 на плоскости
на плоскости 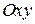 , и систему прямоугольных декартовых координат
, и систему прямоугольных декартовых координат 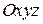 . В каждой точке
. В каждой точке 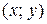
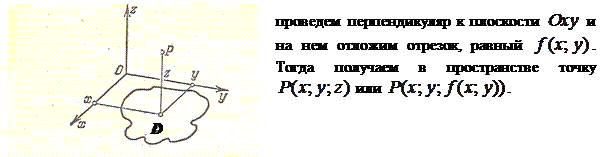
Определение 1.5. Геометрическое место точек 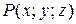 , координаты которых удовлетворяют уравнению
, координаты которых удовлетворяют уравнению  , называется графиком функции двух переменных.
, называется графиком функции двух переменных.
Из курса аналитической геометрии известно, что уравнение  в пространстве определяет некоторую поверхность. Таким образом, графиком функции двух
в пространстве определяет некоторую поверхность. Таким образом, графиком функции двух
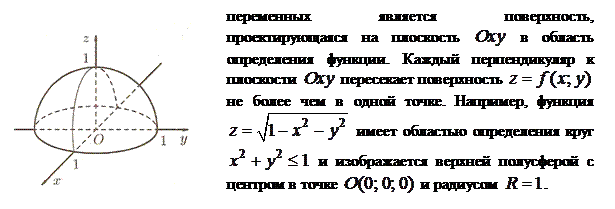
Частные производные ФНП
Рассмотрим линию 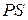 пересечения поверхности
пересечения поверхности  с плоскостью
с плоскостью 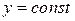 , параллельной плоскости
, параллельной плоскости 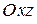 . Так как в этой плоскости
. Так как в этой плоскости  сохраняет постоянное значение, то
сохраняет постоянное значение, то 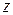 вдоль кривой
вдоль кривой 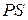 будет меняться только в зависимости от изменения
будет меняться только в зависимости от изменения  . Дадим независимой переменной
. Дадим независимой переменной  приращение
приращение 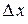 , тогда
, тогда 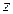 получит приращение, которое называется частным приращением
получит приращение, которое называется частным приращением 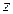 по
по  и обозначают через
и обозначают через 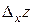 (на рисунке отрезок
(на рисунке отрезок 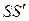 ), так что
), так что
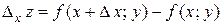 .
.
Аналогично, если  сохраняет постоянное значение, а
сохраняет постоянное значение, а  получает приращение
получает приращение
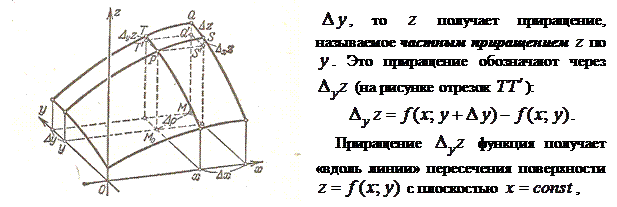
параллельной плоскости 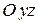 .
.
Наконец, придав аргументу  приращение
приращение 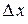 , а аргументу
, а аргументу  приращение
приращение 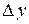 , получим для
, получим для 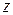 новое приращение
новое приращение 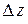 , которое называется полным приращением функции
, которое называется полным приращением функции 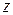 и определяется формулой
и определяется формулой
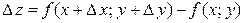 .
.
На рисунке 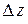 изображено отрезком
изображено отрезком 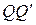 .
.
Надо отметить, что, вообще говоря, полное приращение не равно сумме частных приращений, т.е. 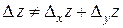 .
.
Определение 2.1. Частной производной по  от функции
от функции  называется предел отношения частного приращения
называется предел отношения частного приращения 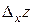 по
по  к приращению
к приращению 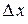 при стремлении
при стремлении 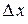 к нулю. Обозначается:
к нулю. Обозначается: 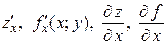 . Тогда
. Тогда
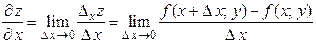 . (2.1)
. (2.1)
Определение 2.2. Частной производной по  от функции
от функции  называется предел отношения частного приращения
называется предел отношения частного приращения 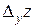 по
по  к приращению
к приращению 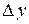 при стремлении
при стремлении 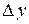 к нулю. Обозначается:
к нулю. Обозначается: 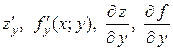 . Тогда
. Тогда
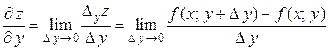 . (2.2)
. (2.2)
Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции  находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно
находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно  или
или  считаются постоянной величиной).
считаются постоянной величиной).
Геометрический смысл частных производных: частная производная 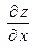 численно равна тангенсу угла наклона a касательной к сечению поверхности
численно равна тангенсу угла наклона a касательной к сечению поверхности  плоскостью
плоскостью 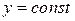 ;
;
частная производная 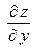 численно равна тангенсу угла наклона b касательной к сечению поверхности
численно равна тангенсу угла наклона b касательной к сечению поверхности  плоскостью
плоскостью 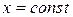 .
.
Пример 2.1. Для данной функции требуется найти частные производные 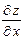 и
и 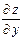 . Найти значения частных производных в точке
. Найти значения частных производных в точке 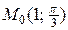 :
:
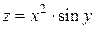 .
.
Решение. Находим частные производные в общем виде:
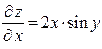 ,
, 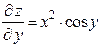 .
.
Находим значения частных производных в точке 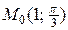 :
:
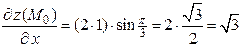 ,
, 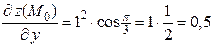 . ,
. ,
Пример 2.2. Найти частные производные 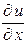 ,
, 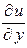 ,
, 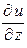 ,
, 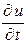 для следующей функции:
для следующей функции:
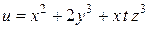 .
.
Решение.
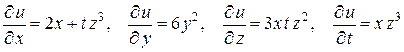 . ,
. ,
В замкнутой области
Пусть функция 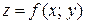 определена и непрерывна в ограниченной замкнутой области
определена и непрерывна в ограниченной замкнутой области 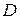 . Тогда она достигает в некоторых точках
. Тогда она достигает в некоторых точках 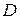 своего наибольшего
своего наибольшего 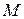 и наименьшего
и наименьшего 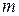 значений (так называемый глобальный экстремум). Эти значения достигаются функцией в точках, расположенных внутри области
значений (так называемый глобальный экстремум). Эти значения достигаются функцией в точках, расположенных внутри области 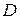 , или в точках, лежащих на границе области.
, или в точках, лежащих на границе области.
В замкнутой области
1. Найти все критические точки функции, принадлежащие 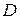 , и вычислить значения функции в них.
, и вычислить значения функции в них.
2. Найти наибольшее и наименьшее значения функции 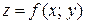 на границах области.
на границах области.
3. Сравнить все найденные значения функции и выбрать из них наибольшее 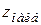 и наименьшее
и наименьшее 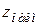 .
.
Пример 3.3. Найти наибольшее и наименьшее значения функции 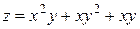 в замкнутой области
в замкнутой области 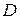 , ограниченной линиями:
, ограниченной линиями: 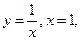
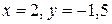 .
.
Решение. 1) Строим замкнутую область 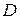 , ограниченную линиями:
, ограниченную линиями: 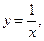
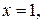
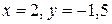 .
.
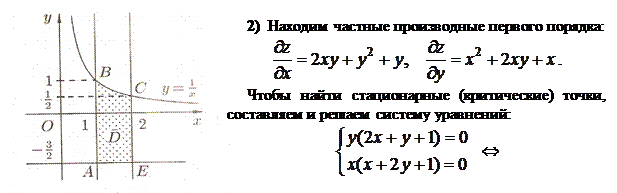
Û 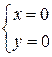 ,
, 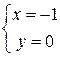 ,
, 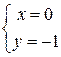 ,
, 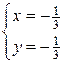 .
.
Таким образом, получаем четыре стационарные точки, ни одна из которых не принадлежит области 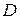 .
.
3) Исследуем функцию на границе области, состоящей из участков 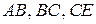 и
и 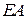 .
.
а) на границу 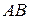 :
: 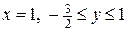 .
.
Тогда получаем функцию от одной переменной  :
: 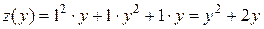 . Находим критические точки:
. Находим критические точки: 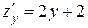 .
.
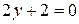 Þ
Þ 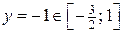 .
.
Далее 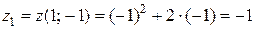 .
.
б) на границу 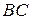 :
: 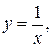
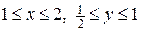 .
.
Тогда получаем функцию от одной переменной  :
: 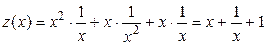 . Находим критические точки:
. Находим критические точки: 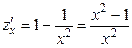 .
.
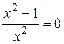 Þ
Þ 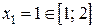 и
и 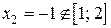 .
.
Далее 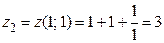 .
.
в) на границу 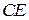 :
: 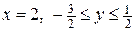 .
.
Тогда получаем функцию от одной переменной  :
: 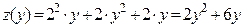 . Находим критические точки:
. Находим критические точки: 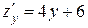 .
.
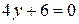 Þ
Þ 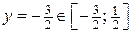 .
.
Далее 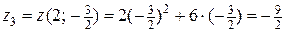 .
.
г) на границу 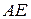 :
: 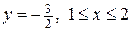 .
.
Тогда получаем функцию от одной переменной  :
:
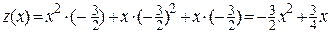 .
.
Находим критические точки: 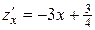 .
.
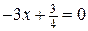 Þ
Þ 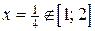 . Значит, на границе
. Значит, на границе 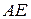 критических точек нет.
критических точек нет.
4) Находим значения функции в вершинах области: 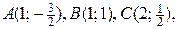
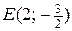 . Выше были найдены значения функции
. Выше были найдены значения функции 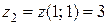 и
и 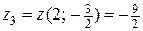 , что соответствует значениям функции в точках
, что соответствует значениям функции в точках 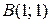 и
и 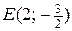 . Поэтому находим значения функции в точках
. Поэтому находим значения функции в точках 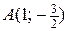 и
и 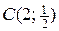 :
:
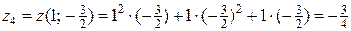 ;
;
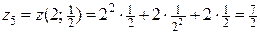 .
.
Из всех полученных значений функции 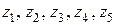 выбираем наибольшее и наименьшее:
выбираем наибольшее и наименьшее:
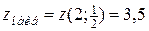 ;
; 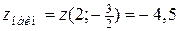 .
.
,
Основные понятия
Функции двух переменных
Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции нескольких переменных.
Например, площадь 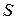 прямоугольника есть функция двух независимо друг от друга изменяющихся переменных – длин сторон прямоугольника
прямоугольника есть функция двух независимо друг от друга изменяющихся переменных – длин сторон прямоугольника  и
и  , которая выражается формулой:
, которая выражается формулой:
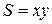 .
.
Работа 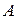 постоянного электрического тока является функцией от разности потенциалов
постоянного электрического тока является функцией от разности потенциалов 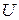 на концах участка, силы тока
на концах участка, силы тока 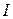 и времени
и времени 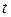 , которая выражается формулой
, которая выражается формулой
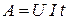 .
.
Например, функция
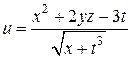
есть функция от четырех переменных 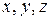 и
и 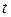 .
.
Остановимся на случае двух переменных, которые будем обозначать  и
и  .
.
Каждой паре значений  и
и  соответствует точка на плоскости
соответствует точка на плоскости 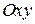 , координатами которой они служат. Рассмотрим некоторое множество точек на плоскости
, координатами которой они служат. Рассмотрим некоторое множество точек на плоскости 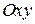 и обозначим его через
и обозначим его через 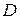 , т.е.
, т.е. 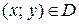 . Надо отметить, что переменные
. Надо отметить, что переменные  и
и  не зависимы друг от друга.
не зависимы друг от друга.
Определение 1.1. Если каждой паре 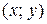 из некоторой области их изменения
из некоторой области их изменения 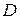 , поставлено в соответствие определенное значение величины
, поставлено в соответствие определенное значение величины 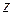 , то говорят, что
, то говорят, что 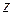 есть функция двух независимых переменных
есть функция двух независимых переменных  и
и  . Записывается
. Записывается
 .
.
При этом  и
и  называются независимыми переменными (аргументами), а
называются независимыми переменными (аргументами), а 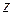 - зависимой переменной (функцией).
- зависимой переменной (функцией).
Определение 1.2. Множество пар 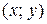 значений
значений  и
и  , при которых определена функция
, при которых определена функция  , называется областью определения функции, обозначается
, называется областью определения функции, обозначается 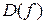 .
.
Если каждую пару значений  и
и  можно изобразить точкой на плоскости
можно изобразить точкой на плоскости 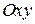 , то область определения функции изобразиться в виде некоторой совокупности точек этой плоскости. В частности, область определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями.
, то область определения функции изобразиться в виде некоторой совокупности точек этой плоскости. В частности, область определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями.
Определение 1.3. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой.
Пример 1.1. Найти область определения 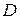 функции
функции
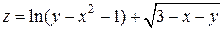 .
.
Решение. Областью определения данной функции является множество точек плоскости 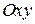 , которые удовлетворяют решению системе неравенств
, которые удовлетворяют решению системе неравенств
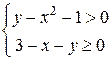 .
.

,
Определение функции двух переменных легко обобщить на случай трех или более переменных.
Определение 1.4. Если каждой рассматриваемой совокупности значений переменных 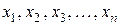 соответствует определенной значение переменной
соответствует определенной значение переменной 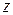 , то
, то 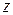 называют функцией независимых переменных
называют функцией независимых переменных 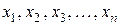 и записывают
и записывают
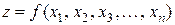 .
.
Так же как и для функции двух переменных, можно говорить об области определения функции трех, четырех и более переменных. Так, например, для функции трех переменных областью определения является некоторая совокупность троек чисел 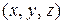 , которые представляют совокупность точек пространства. Область определения функции четырех и более числа переменных уже не допускает простого геометрического истолкования.
, которые представляют совокупность точек пространства. Область определения функции четырех и более числа переменных уже не допускает простого геометрического истолкования.
Функция двух переменных, как и функция одной переменной, может быть задана разными способами: таблицей, аналитически, графически.
Рассмотрим функцию  , определенную в области
, определенную в области 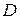 на плоскости
на плоскости 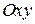 , и систему прямоугольных декартовых координат
, и систему прямоугольных декартовых координат 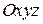 . В каждой точке
. В каждой точке 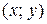
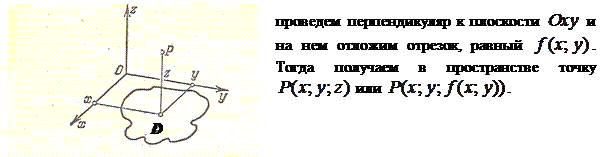
Определение 1.5. Геометрическое место точек 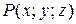 , координаты которых удовлетворяют уравнению
, координаты которых удовлетворяют уравнению  , называется графиком функции двух переменных.
, называется графиком функции двух переменных.
Из курса аналитической геометрии известно, что уравнение  в пространстве определяет некоторую поверхность. Таким образом, графиком функции двух
в пространстве определяет некоторую поверхность. Таким образом, графиком функции двух
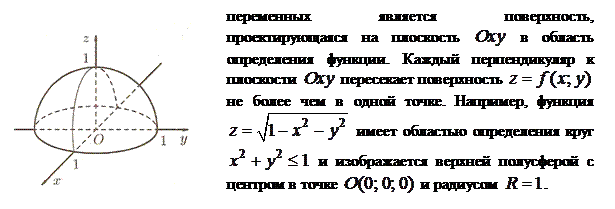
Предел и непрерывность функции двух переменных
Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывность, аналогично случаю функции одной переменной.
Введем понятие окрестности точки.
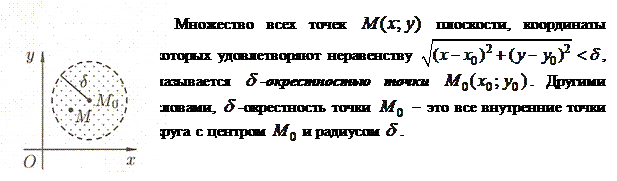
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки 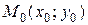 , кроме, может быть, самой этой точки.
, кроме, может быть, самой этой точки.
Определение 1.6. Число 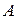 называется пределом функции
называется пределом функции  при
при 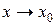 и
и 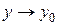 (или, что то же самое, при
(или, что то же самое, при 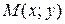 ®
® 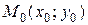 ), если для любого
), если для любого 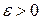 существует
существует 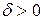 такое, что для всех
такое, что для всех 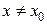 и
и 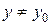 и, удовлетворяющих неравенству
и, удовлетворяющих неравенству 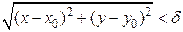 , выполняется неравенство
, выполняется неравенство 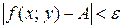 . Записывают:
. Записывают:
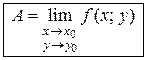 (1.1)
(1.1)
или
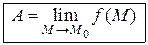 .
.
Из определения следует, что если предел существует, то он не зависит от пути, по которому 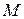 стремится к
стремится к 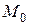 (число таких направлений бесконечно). Определения бесконечно малых и бесконечно больших величин являющихся функциями двух переменных, аналогичны соответствующим определениям для функций одной переменной.
(число таких направлений бесконечно). Определения бесконечно малых и бесконечно больших величин являющихся функциями двух переменных, аналогичны соответствующим определениям для функций одной переменной.
Геометрический смысл предела функции двух переменных состоит в следующем. Каково бы ни было число 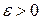 , найдется
, найдется 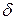 -окрестность точки
-окрестность точки 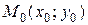 , что во всех точках
, что во всех точках 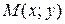 , отличных от
, отличных от 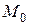 , аппликаты соответствующих точек поверхности
, аппликаты соответствующих точек поверхности  отличаются от числа
отличаются от числа 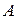 по модулю меньше, чем на
по модулю меньше, чем на 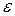 .
.
Пример 1.2. Найти предел 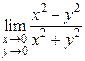 .
.
Решение. Будем приближаться к 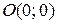 по прямой
по прямой 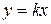 , где
, где 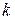 - некоторое число. Тогда
- некоторое число. Тогда
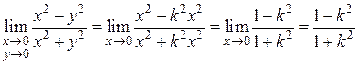 .
.
Функция 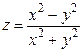 в точке
в точке 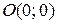 предела не имеет, т.к. при разных значениях
предела не имеет, т.к. при разных значениях 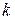 предел функции не одинаковый (функция имеет различные предельные значения).
предел функции не одинаковый (функция имеет различные предельные значения).
,
Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной.
Определение 1.7. Функция  (или
(или 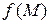 ) называется непрерывной в точке
) называется непрерывной в точке 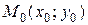 , если она:
, если она:
1) определена в этой точке и некоторой ее окрестности;
2) имеет предел 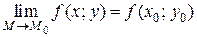 ;
;
3) этот предел равен значению функции 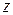 в точке
в точке 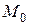 , т.е.
, т.е.
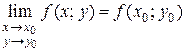 или
или 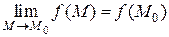 .
.
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке), называются точками разрыва этой функции. Точки разрыва  могут образовывать целые линии разрыва. Так, например, функция
могут образовывать целые линии разрыва. Так, например, функция 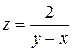 имеет линю разрыва
имеет линю разрыва 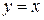 .
.
Можно дать другое, равносильное приведенному выше, определение непрерывности функции  в точке. Обозначим
в точке. Обозначим 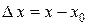 ,
, 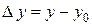 . Значит,
. Значит, 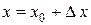 и
и 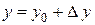 . Величины
. Величины 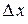 и
и 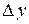 называются приращениями аргументов
называются приращениями аргументов  и
и  . Тогда
. Тогда 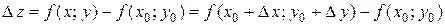 . Величина
. Величина 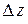 называется полным приращением функции
называется полным приращением функции  в точке
в точке 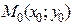 .
.
Определение 1.8. Функция  называется непрерывной в точке
называется непрерывной в точке 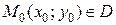 , если полное приращение функции в этой точке стремится к нулю, когда приращения ее аргументов
, если полное приращение функции в этой точке стремится к нулю, когда приращения ее аргументов  и
и  стремятся к нулю, т.е.
стремятся к нулю, т.е.
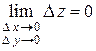 .
.
Пользуясь определением непрерывности и теоремами о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям – подобные теоремы имели для функций одной переменной.
2. ДИФФЕРЕНЦИРОВАНИЕ ФНП
Частные производные ФНП
Рассмотрим линию 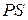 пересечения поверхности
пересечения поверхности  с плоскостью
с плоскостью 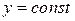 , параллельной плоскости
, параллельной плоскости 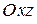 . Так как в этой плоскости
. Так как в этой плоскости  сохраняет постоянное значение, то
сохраняет постоянное значение, то 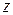 вдоль кривой
вдоль кривой 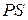 будет меняться только в зависимости от изменения
будет меняться только в зависимости от изменения  . Дадим независимой переменной
. Дадим независимой переменной  приращение
приращение 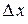 , тогда
, тогда 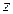 получит приращение, которое называется частным приращением
получит приращение, которое называется частным приращением 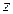 по
по  и обозначают через
и обозначают через 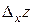 (на рисунке отрезок
(на рисунке отрезок 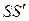 ), так что
), так что
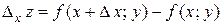 .
.
Аналогично, если  сохраняет постоянное значение, а
сохраняет постоянное значение, а  получает приращение
получает приращение
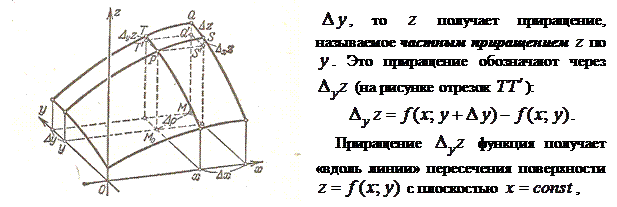
параллельной плоскости 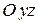 .
.
Наконец, придав аргументу  приращение
приращение 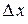 , а аргументу
, а аргументу  приращение
приращение 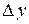 , получим для
, получим для 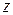 новое приращение
новое приращение 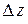 , которое называется полным приращением функции
, которое называется полным приращением функции 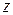 и определяется формулой
и определяется формулой
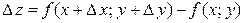 .
.
На рисунке 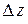 изображено отрезком
изображено отрезком 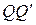 .
.
Надо отметить, что, вообще говоря, полное приращение не равно сумме частных приращений, т.е. 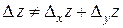 .
.
Определение 2.1. Частной производной по  от функции
от функции  называется предел отношения частного приращения
называется предел отношения частного приращения 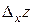 по
по  к приращению
к приращению 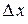 при стремлении
при стремлении 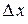 к нулю. Обозначается:
к нулю. Обозначается: 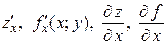 . Тогда
. Тогда
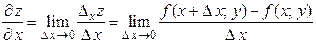 . (2.1)
. (2.1)
Определение 2.2. Частной производной по  от функции
от функции  называется предел отношения частного приращения
называется предел отношения частного приращения 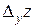 по
по  к приращению
к приращению 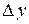 при стремлении
при стремлении 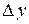 к нулю. Обозначается:
к нулю. Обозначается: 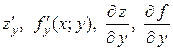 . Тогда
. Тогда
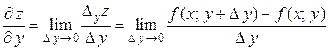 . (2.2)
. (2.2)
Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции  находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно
находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно  или
или  считаются постоянной величиной).
считаются постоянной величиной).
Геометрический смысл частных производных: частная производная 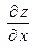 численно равна тангенсу угла наклона a касательной к сечению поверхности
численно равна тангенсу угла наклона a касательной к сечению поверхности  плоскостью
плоскостью 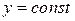 ;
;
частная производная 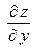 численно равна тангенсу угла наклона b касательной к сечению поверхности
численно равна тангенсу угла наклона b касательной к сечению поверхности  плоскостью
плоскостью 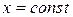 .
.
Пример 2.1. Для данной функции требуется найти частные производные 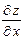 и
и 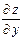 . Найти значения частных производных в точке
. Найти значения частных производных в точке 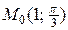 :
:
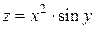 .
.
Решение. Находим частные производные в общем виде:
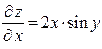 ,
, 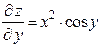 .
.
Находим значения частных производных в точке 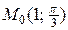 :
:
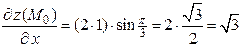 ,
, 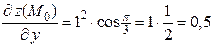 . ,
. ,
Пример 2.2. Найти частные производные 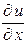 ,
, 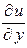 ,
, 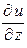 ,
, 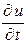 для следующей функции:
для следующей функции:
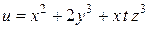 .
.
Решение.
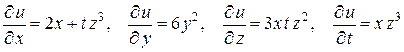 . ,
. ,
&n
