Основные элементарные функции и их графики

Основными элементарными функциями называются функции, которые имеет следующий вид, и на рисунках представлены их графики.

1. Линейная функция

Функция вида y=ax+b, где a, bÎR называется линейной функцией.

Графиком линейной функции является прямая. Для построения прямой достаточно знать координаты двух точек, например, A(0; b) и 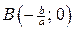, если a¹0.

Коэффициент k называют угловым коэффициентом прямой – графика функции y=kx+b.

2. Квадратичная функция

Функция вида 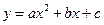, где a, b, cÎR, называется квадратичной функцией.

Графиком квадратичной функции является парабола.

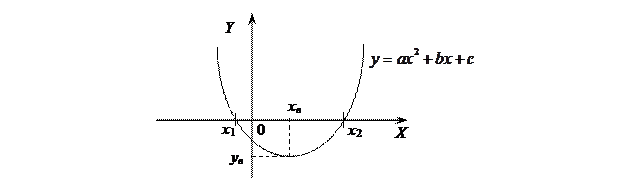
a>0 – ветви параболы направлены вверх; a<0 – ветви параболы направлены вниз.

Точка (x_в; y_в) – вершина параболы, .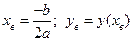

Прямая x=x_в – ось симметрии.

x₁, x₂ – корни квадратного уравнения .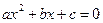

3. Обратная пропорциональность

Функция вида 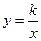, где k≠0, x≠0 называется обратной пропорциональностью.

Графиком данной функции является гипербола.

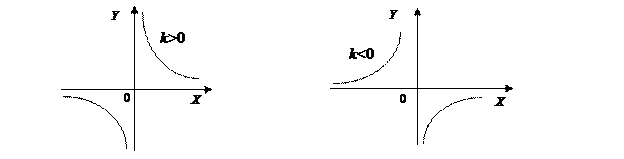
4. Степенные функции

1). Степенная: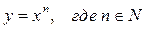

2). Степенная: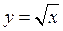

5. Показательные функции

Функция, заданная формулой y=a^x, где a>0, a¹1, называется показательной функцией с основанием a.

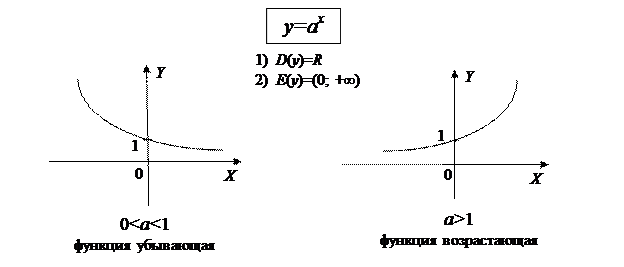
6. Логарифмические функции

Функция, заданная формулой 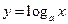называется логарифмической функцией с основанием a.

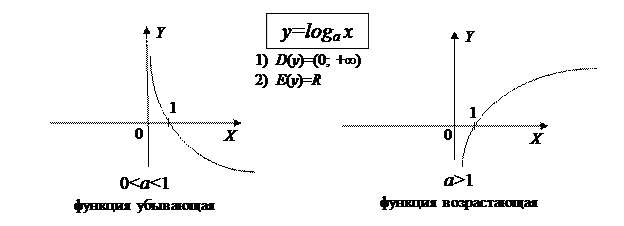
7. Тригонометрические функции

Тригонометрическими функциями называются функции вида , , , .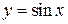

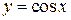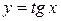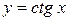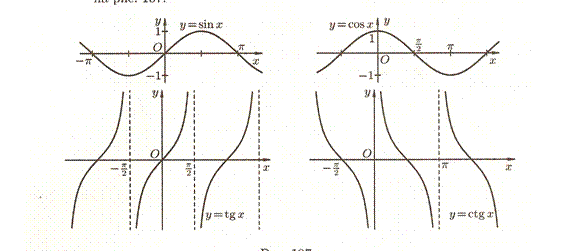
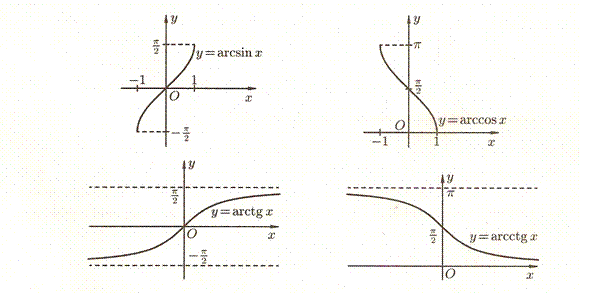
8. Обратные тригонометрические функции

Обратными тригонометрическими функциями называются функции вида , , , .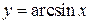

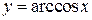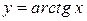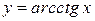Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операций взятия функции от функции, называются элементарными функциями. Например, следующие функции являются элементарными:

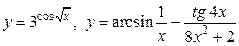
Примерами неэлементарных функций могут служить функции:

.

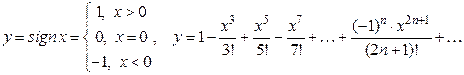2. ПРЕДЕЛ ФУНКЦИИ

2.1. Предел функции в точке

Пусть функция определена на некотором числовом множестве X и точка является предельной точкой этого множества, т.е. в любой e-окрестности точки содержатся точки множества X, отличных от . Точка может принадлежать множеству X или не принадлежать ему, следовательно, функция либо определена в точке , либо не определена.

Определение 2.1 (на «языке e-d», или по Коши).

Число A называется пределом функции в точке (или при 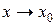), если для любого положительного e найдется такое положительное число d, что для всех 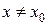, удовлетворяющих неравенству 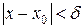, выполняется неравенство .

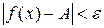С помощью логических символов это определение можно записать следующим образом:

.

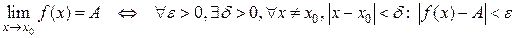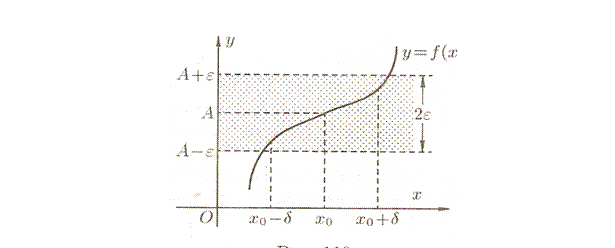
Геометрический смысл предела функции: 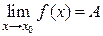, если для любой e-окрестности точки A найдется такая d-окрестность точки , что для всех 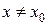из этой d-окрестности соответствующие значения функции 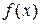лежат в e-окрестности точки A. Иными словами, точки графика функции лежат внутри полосы шириной 2e, ограниченной прямыми 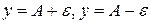. Очевидно, что величина d зависит от выбора e, поэтому пишут .

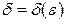Еще раз подчеркнем, что при решении вопроса о существовании предела функции f в точке сама точка из рассмотрения исключается, а функция f считается определенной в некоторой достаточно малой окрестности точки . В этом смысле свойство функции иметь предел в точке является локальным свойством функции.

2.2. Предел функции при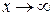

Сформулируем понятие предела функции при 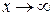, т.е. когда x неограниченно возрастает по модулю.

Определение 1.2. Число A называется пределом функции при 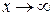, если для любого положительного e существует такое положительное число 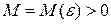, что при всех 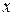, удовлетворяющих неравенству 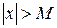, выполняется неравенство .

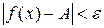С помощью логических символов это определение можно записать следующим образом:

.

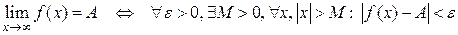Если 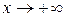, то пишут 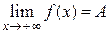; если 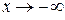, то пишут .

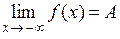Например, 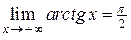, а .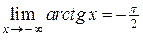

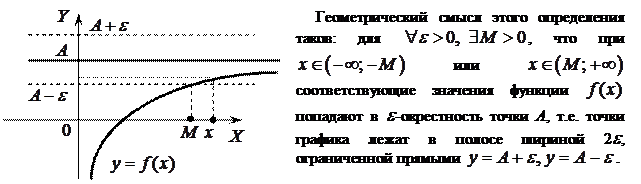
2.3. Бесконечно большая функция (б.б.ф.)

Определение 2.3. Функция называется бесконечно большой (б.б.ф.) при 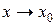, если для любого числа 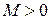существует число 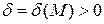, что для всех 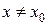, удовлетворяющих неравенству 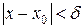, выполняется неравенство 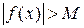, т.е.

.

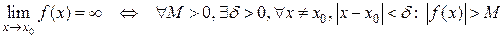Если 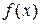стремится к бесконечности при 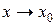и принимает лишь положительные значения, то пишут 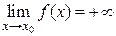; если лишь отрицательные значения, то .

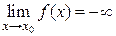Пример 2.2. Показать, что функция 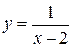является бесконечно большой при .

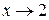Решение. Найдем предел функции пр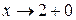и и :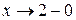

; .

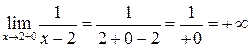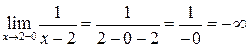Значит, данная функция является бесконечно большой при . ,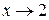

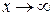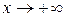Аналогично определяются бесконечно большие функции (т.е. понятия бесконечного предела функции) при , или , или .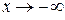

Пример 2.3. Показать, что функция 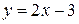является бесконечно большой при .

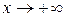Решение. Найдем предел функции при :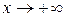

.

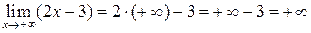Значит, данная функция является бесконечно большой при .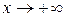

,

Свойства б.б.ф.

1) Сумма любого числа б.б.ф. одного знака есть б.б.ф.

2) Произведение б.б.ф. на функцию, ограниченную в данном процессе, есть б.б.ф.

3) Произведение постоянной величины и б.б.ф. есть б.б.ф.

4) Произведение двух б.б.ф. есть б.б.ф.

5) Отношение б.б.ф. и величины, ограниченной в данном процессе, но не равной 0, есть б.б.ф.

2.4. Бесконечно малая функция (б.м.ф.)

Определение 2.4. Функция 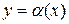называется бесконечно малой (б.м.ф.) при 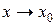, если для любого положительного e найдется такое положительное число d, что для всех 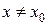, удовлетворяющих неравенству 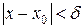, выполняется неравенство .

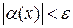С помощью логических символов это определение можно записать следующим образом:

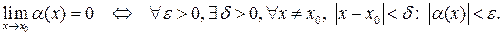
Пример 2.4. Показать, что функция 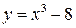является бесконечно малой при .

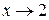Решение. Найдем предел функции при :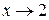

.

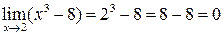Значит, данная функция является бесконечно малой при .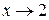

,

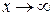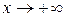Аналогично определяются бесконечно малые функции (т.е. понятия бесконечного предела функции) при , или , или .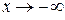

Бесконечно малые функции называют бесконечно малыми величинами или бесконечно малыми; обозначают обычно греческими буквами, т.е. .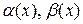

Свойства б.м.ф.

1) Алгебраическая сумма конечного числа б.м.ф. есть б.м.ф.

2) Произведение ограниченной функции на б.м.ф. есть функция бесконечно малая.

3) Произведение двух б.м.ф. есть функция бесконечно малая.

4) Произведение б.м.ф. на число есть функция бесконечно малая.

5) Частное от деления б.м.ф. на функцию, имеющую отличный от нуля предел, есть б.м.ф.

6) Теорема 2.1. Если 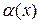- б.м.ф. ( 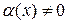) при 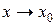, то функция 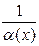есть б.б.ф. Если функция 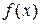- б.б.ф., то 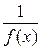есть б.м.ф.

Теорему примем без доказательства.

Например, функция 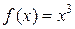б.м.ф. при 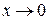, тогда функция 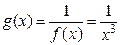есть б.б.ф. при .

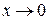Пример 2.5. Показать, что функция 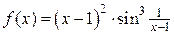при 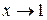является бесконечно малой.

Решение. Так как 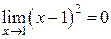, то функция 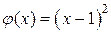есть бесконечно малая при 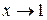. Функция 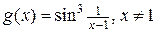, ограничена, т.к. .

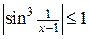Функция 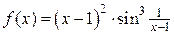представляет собой произведение ограниченной функции 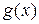на бесконечно малую 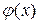. Значит, 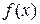- бесконечно малая при .

,

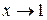3. ПРОИЗВОДНАЯ ФУНКЦИИ